Некоторые сведения из механики разрушения

Наука о поведении тел с трещинами называется механикой разрушения. Трещина обычно рассматривается как разрез нулевой ширины с острой вершиной. В зависимо­сти от конфигурации и расположения в теле трещины мо­гут быть сквозные краевые, сквозные внутренние, поверх­ностные или внутренние объемные (рис. 11.1, а—г). Тело с трещиной может нагружаться одним из трех способов: нормальный отрыв (тип /), поперечный относительно фронта трещины сдвиг (тип II) и продольный сдвиг (тип III), или их комбинацией (рис. 11.1, д). Наибольший инте­рес для прогнозирования процессов распространения усталостных и хрупких трещин в элементах конструк­ций представляет модель трещины нормального отрыва (тип I).

Трещина является предельно острым концентратором. При нагружении тела вокруг ее вершины формируется область повышенных напряжений. Раздел механики разрушения, в рамках которого рассматриваются модели тел из идеально упругого материала, называется линейной механикой разрушения. Более сложные модели, учитывающие пластические деформации в зоне концентрации напряжений у вершины трещины, составляют объект изучения не­линейной или упругопластической механики разрушения.

Условие распространения трещины в твердом упругом теле на основе анализа энергетического баланса предло­жил Алан Грифитс в 1921 г. Для этой задачи энергетиче­ское условие равновесия (3.2) запишется как

(11.1)

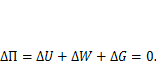
Здесь AG— затраты энергии на разрушение материала в вершине трещины при ее продвижении на малую вели­чину Аа « а.

Рассмотрим абсолютно упругую полосу толщиной tс краевой трещиной длиной а « В (рис. 11.2). При нагру­жении полосы силой Fв ней возникнут номинальные на­пряжения а и она получит удлинение 5. Закрепим ее край в этом положении (состояние 1) и проанализируем возмож­ность развития трещины. Упрощая картину напряженно­го состояния полосы, будем считать, что трещина вызы-

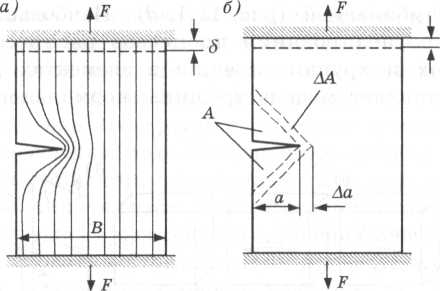Рис. 11.2. Схемы к энергетическому анализу развития трещины

вает разгрузку материала в зонеА, то есть здесь напряже­ния близки к нулю (на рис. 11.2, а показаны линии «пото­ков напряжений»). Зададим «возможное перемещение» (п. 3.1.1) в виде малого приращения длины трещины на Да (состояние 2). При этом номинальные напряжения в пластине и концентрация напряжений в ее вершине из­менятся пренебрежимо мало, а зона разгрузки увеличится на 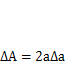(рис. 11.2, б). Внешние силы при этом не совершают работы, так как кромки пластины закреплены ( U= 0). Часть полосы разгружается, следовательно, внут­ренние силы совершают положительную работу

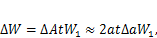
где 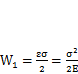удельная потенциальная энергияупругой деформации.

Энергия разрушения материала при увеличении площади трещины на составит 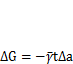, где — удельная энергия разрушения материала, Н м/м². Энергия Gот­рицательна, так как она затрачивается на разрушение. Подставив полученные выражения в (11.1), найдем 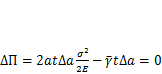— условие равновесия трещины.

Если получится 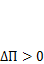, то трещина будет развиваться, так как высвобождаемой упругой энергии окажется достаточно для разрушения материала в вершине трещи­ны. При 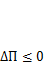трещина развиваться не будет. Отсюда получим условие нераспространения трещины

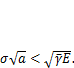
В левой части этого условия стоит величина, пропорци­ональная выделяемой упругой энергии и зависящая от нагруженности материала в вершине трещины. Правая часть характеризует затраты энергии на продвижение трещи­ны, т. е. трещиностойкость материала. Она зависит от свойств материала, условий деформирования и определя­ется экспериментальным путем. Удельная энергия разру­шения для пластичного материала существенно боль­ше, чем для хрупкого, который до разрушения сохраняет упругий характер деформирования.

Приведенный простейший пример показывает только структуру условия трещиностойкости. При решении этой задачи методами теории упругости и механики разруше­ния нагруженность материала в вершине трещины нор­мального отрыва (тип I) характеризует коэффициент ин­тенсивности напряжений (КИН)

(11.2)

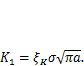
Здесь — безразмерный коэффициент, зависящий от гео­метрии тела и называемый .К-тарировкой; — номиналь­ные напряжения в сечении с трещиной, вычисленные по сечению брутто (т. е. без учета трещины, при а = 0); а — характерный размер трещины (рис. 11.2). КИН является базовым понятием механики разрушения. Он имеет раз­мерность 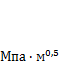. В зарубежной литературе используют другие единицы:

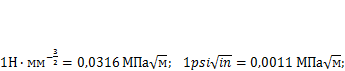
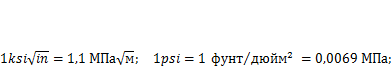
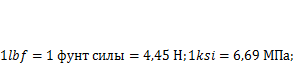
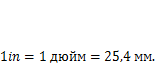
В идеально упругом теле с трещиной нормального от­рыва (тип I) распределение напряжений по сечению с тре­щиной вблизи ее вершины описывается классическим ре­шением теории упругости (рис. 11.3, а):

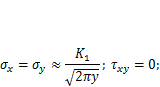
(11.3)

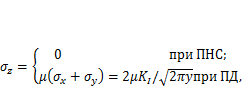
где — коэффициент Пуассона; ПНС — плоское (т. е. двух­осное) напряженное состояние, которое реализуется, например, в сравнительно тонком листе со сквозной трещи­ной; ПД — состояние плоской деформации, при котором

отсутствуют деформации металла вдоль оси zза счет дей­ствия третьей компоненты напряженного состояния . Состояние ПД возникает в вершине трещины, расположен­ной в детали большой толщины (рис. 11.3, б). Знак при­ближенного равенства в формулах означает, что в данном решении отброшены последующие члены ряда, имеющие существенное значение вдали от вершины и мало влия­ющие на распределение напряжений вблизи нее.

Перемещение берегов трещины вблизи ее вершины вы­числяется как

(11.4)

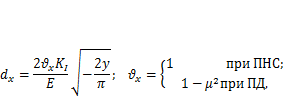
гдеЕ — модуль упругости материала. На берегах трещи­ны (рис. 11.3, а).

Как видно из (11.3), при напряжения бесконечно возрастают. Однако это возможно только теоретически в мо­дели из идеально упругого материала. В детали из реального материала в вершине трещины образуется пластическая зона или разрушение. Если пластическая зона не велика по сравне­нию с размером а, ее размер также зависит от КИН и условий деформирования материала вблизи вершины трещины.

Условия плоской деформации существенно затрудняют развитие пластических деформаций, что способствует раз­витию хрупкого разрушения (п. 7.3). В этом можно убе­диться путем анализа условия текучести 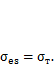Эквива­лентные напряжения на малом расстоянии уот вершины трещины вычисляются по формуле (7.5), куда подставим

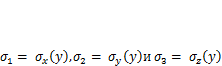из (11.3). При ПНС эк­вивалентные напряжения составляют 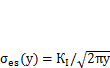, а при ПД — 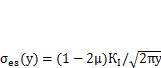.То есть в условиях плоского напряженного состояния пластические деформа­ции происходят при достижении 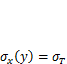, а при плоской деформации — при 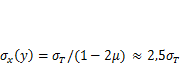. Следовательно, при одинаковом уровне номинальных напряжений пла­стическая зона в условиях плоской деформации будет иметь значительно меньший размер, чем при плоском напряжен­ном состоянии (рис. 11.3, в), а уровень напряжений будет существенно выше. Это свидетельствует о том, что развитие трещины в тонкостенном элементе будет про­исходить при значительных пластических деформациях, а в толстостенных — скорее по хрупкому механизму.