Методы анализа напряженно-деформированного состояния конструкций
Большинство инженерных условий работоспособности строится в форме сравнения напряжений. Для вычисления напряжений необходимо построить соответствующую модель конструкции. Графическое представление конфигурации конструкции, ее закреплений и распределения нагрузок представляет собой геометрическую модель, которую называют расчетной схемой (рис. 2.2). Математическое описание свойств и поведения исследуемого объекта, процессов, протекающих в нем, является математической моделью. В зависимости от вида расчетного критерия и особенностей конструкции модель может быть общей или локальной, т. е. включающей только некоторый фрагмент конструкции. Для получения оптимальной модели в ее состав следует включать только те элементы системы, которые существенно влияют на значения искомых величин и граничные условия для которых могут быть заданы достаточно надежно.
Распределение напряжений в конструкции зависит от внешних воздействий, свойств материала и геометрии конструкции.
Свойства материала при анализе напряженного состояния характеризуют диаграммой деформирования, т. е. зависимостью напряженийа от относительных деформаций материала 8 при одноосном напряженном состоянии. Реальная диаграмма деформирования (рис. 1.2, а), которая может иметь площадку текучести (кривая 1) или не иметь (кривая 2), заменяется упрощенной схемой. Простейшим вариантом схематизации является модель идеально упругого материала (рис. 1.2, б, кривая 3)
 (1.5)
(1.5)
Для учета пластичности используют модель идеально упруго-пластического материала (диаграмма Прандтля, рис. 1.2, б, кривая 4)
 (1.6)
(1.6)
Упрочнение стали при пластическом деформировании описывает модель упругопластического материала с линейным упрочнением (кривая 5)
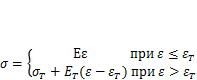 (1.7.)
(1.7.)
или со степенным упрочнением (кривая 6)
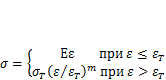 (1.8)
(1.8)
ЗдесьЕ — модуль упругости;  — модуль упрочнения,
— модуль упрочнения, 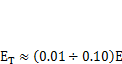 ;
;  — предел текучести;
— предел текучести; 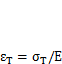 ;
;  — показатель упрочнения, для конструкционных сталей
— показатель упрочнения, для конструкционных сталей 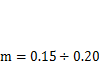 .
.
Реальное распределение напряжений в конструкции имеет весьма сложный вид. Для его анализа применяют аналитические, численные или экспериментальные методы, которые обладают разными возможностями и позволяют получить разный уровень приближения или детализации оценки поля напряжений. Уровень требуемой детализации расчетной оценки, т. е. приближения к реальности, зависит от того, для какого критерия работоспособности конструкции используется эта оценка. Можно выделить три уровня детализации при расчете напряженно-деформированного состояния.
I. Общее напряженное состояние стержневых конструкций, которое описывается методами технической теории изгиба балок. Напряжения, полученные таким способом, называют номинальными (рис. 1.3, а, напряжения  ). Распределение этих напряжений согласно принципу Сен-Венана не зависит от локальных особенностей и способа приложения нагрузок, концентрации напряжений и пр. Параметры общего напряженного состояния могут быть найдены аналитически или с помощью МКЭ по стержневым конечно-элементным моделям. Максимальные номинальные напряжения используют для расчетов на прочность и устойчивость при выборе основных параметров сечения балок и элементов ферм.
). Распределение этих напряжений согласно принципу Сен-Венана не зависит от локальных особенностей и способа приложения нагрузок, концентрации напряжений и пр. Параметры общего напряженного состояния могут быть найдены аналитически или с помощью МКЭ по стержневым конечно-элементным моделям. Максимальные номинальные напряжения используют для расчетов на прочность и устойчивость при выборе основных параметров сечения балок и элементов ферм.
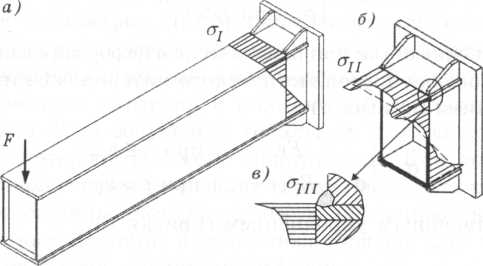 Рис. 1.3. Пример трех уровней описания напряженного состояния элемента конструкции Рис. 1.3. Пример трех уровней описания напряженного состояния элемента конструкции |
II. Местное напряженное состояние нижнего уровня характеризует нагруженность материала вблизи галтелей, вырезов и люков, в области присоединения элементов, приложения местной нагрузки и пр. (рис. 1.3, б, напряжения  ). Местное возмущение напряженного состояния этого уровня охватывает области размером не менее 0,1В (В — характерный размер поперечного сечения). Оценки напряженного состояния нижнего уровня выполняются МКЭ с применением плоских (2D) или объемных (3D) конечных элементов (п. 4.5). Отдельные задачи имеют аналитическое решение, полученное с использованием аппарата теории упругости. Параметры напряжений этого уровня фигурируют в условиях прочности и сопротивления усталости сварных узлов.
). Местное возмущение напряженного состояния этого уровня охватывает области размером не менее 0,1В (В — характерный размер поперечного сечения). Оценки напряженного состояния нижнего уровня выполняются МКЭ с применением плоских (2D) или объемных (3D) конечных элементов (п. 4.5). Отдельные задачи имеют аналитическое решение, полученное с использованием аппарата теории упругости. Параметры напряжений этого уровня фигурируют в условиях прочности и сопротивления усталости сварных узлов.
III. Местное напряженное состояние верхнего уровня связано с концентрацией напряжений от конфигурации сварного шва или отверстия, загруженного болтом, и имеет характерный размер порядка толщины используемого проката (рис. 1.3, в напряжения  ). Этот уровень детализации может быть получен МКЭ. Параметры этого уровня не фигурируют в инженерных расчетах на прочность и устойчивость, а в расчетах на сопротивление усталости учитываются значением предела выносливости.
). Этот уровень детализации может быть получен МКЭ. Параметры этого уровня не фигурируют в инженерных расчетах на прочность и устойчивость, а в расчетах на сопротивление усталости учитываются значением предела выносливости.
Следует подчеркнуть, что напряженное состояние реальной конструкции представляет собой единое поле, а данная классификация условна и относится не к полям действующих напряжений, а к методам их моделирования (расчета). Далее при описании критериев работоспособности будет указано, какого уровня детализация требуется при моделировании напряженного состояния.
Аналитические методы представляют собой замкнутые алгоритмы вычисления параметров напряженно-деформированного состояния конструкции. В большинстве случаев в аналитических расчетах используют стержневые модели, по которым с помощью технической теории изгиба стержней Бернулли—Эйлера (гипотеза плоских сечений) получают оценки общего напряженного состояния и упругих перемещений элементов конструкции.
Основным достоинством аналитических методов является их общность, позволяющая во многих случаях проанализироватьвлияние отдельных аргументов, найти оптимальное решение, сформулировать универсальные конструктивные рекомендации. Кроме того, аналитические методы полезны для понимания процессов, происходящих в конструкции. В связи с этим в данной книге аналитическим методам уделено основное внимание.
Численное моделирование с помощью МКЭ дает возможность рассчитывать конструкции сколь угодно сложной конфигурации, при любых видах нагрузок и при необходимости без учета вышеуказанных допущений (п. 1.5.1). В зависимости от выбранных типов конечных элементов и детальности конечно-элементной модели этот метод позволяет выполнить моделирование напряженно-деформированного состояния в рамках принятых допущений с любой точностью (п. 4.5). В отличие от аналитического метода МКЭ дает решение только для конкретного узла с заданной геометрией и не позволяет строить обобщенные выводы.
Экспериментальные методы используют для исследования действительного напряженно-деформированного состояния элементов конструкций. Они существенно более трудоемки, чем аналитические и численные. Экспериментальные методы эффективны для получения информации о напряженном состоянии конкретных узлов в условиях дефицита данных для расчетной оценки:
• при реальном эксплуатационном нагружении (с учетом фактической загруженности приводов, изменения условий опирания конструкции и т. п.);
• под влиянием несовершенств конструкции (неравномерности и степени затяжки болтов, сварочных поводок, условий контакта элементов, погрешности сборки конструкции и пр.);
• при исследовании остаточных сварочных напряжений и др.
Существует целый ряд методов экспериментального исследования напряженно-деформированного состояния конструкций, но чаще всего применяют тензометрический метод. Для повышения надежности результатов эксперимента целесообразно сочетать его с аналитическими и численными исследованиями конструкции.
Глава 2. СТАТИЧЕСКИ ОПРЕДЕЛИМЫЕ СТЕРЖНЕВЫЕ СИСТЕМЫ (аналитические методы расчета)
Модели стержневых систем
Основные понятия и допущения
Для прогнозирования работоспособности конструкции необходимо иметь методику вычисления действующих напряжений и упругих перемещений, которые являются функциями внутренних усилий, возникающих в конструкции под воздействием нагрузок. Для определения внутренних усилий и перемещений элементов стержневой конструкции необходимо построить модель, которая включает статическую схему и математическое описание ее напряженно-деформированного состояния. Стержневые расчетные схемы могут быть плоскими или пространственными. Плоскими называют схемы, в которых все стержни и действующие нагрузки лежат в одной плоскости. Аналитические методы обычно используют только для расчета плоских или простейших пространственных схем.
В стержневых расчетных схемах стержень изображается линией, проходящей через центры тяжести его сечений (рис. 2.1, линия 1). Точки приложения нагрузок или закреплений, не лежащие на оси стержня, соединяют с основным стержнем 1 вспомогательными абсолютно жесткими стержнями 2.
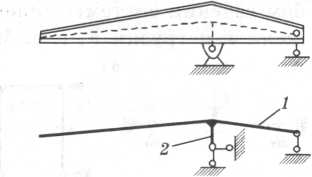 |
| Рис.2.1. К созданию расчетной схемы конструкции |
Обозначения опорных связей, принятые в строительной механике, приведены в п. 2.1.2. При аналитическом расчете ПО Данной стержневой модели вычисляютсясначала внутренние усилия, а потом с помощью технической теории изгиба балок — напряжения и перемещения.
Инженерные аналитические методы расчета стержневых систем базируются на ряде допущений, обеспечивающих существенное упрощение алгоритма вычислений без заметного снижения точности результата.
Линейные системы. Для того чтобы несущая конструкция могла выполнять свои функции, обеспечивать нормальную работу механизмов и рабочих органов, ее необходимо спроектировать так, чтобы она обладала достаточно высокой жесткостью и не получала остаточных деформаций под действием эксплуатационных нагрузок. Эти требования позволяют сформулировать следующие два допущения, на основе которых строится большинство инженерных моделей стальных конструкций.
1. Упругие перемещения элементов конструкции под действием эксплуатационных нагрузок весьма малы по сравнению с размерами их сечений. Это свойство называется геометрической линейностью. Оно позволяет вычислять внутренние усилия в элементах системы без учета упругих перемещений. Примеры геометрически линейных и нелинейных систем показаны на рис. 2.2.
2. Материал конструкции является абсолютно упругим, т. е. подчиняется закону Гука, и имеет одинаковые модули упругости при растяжении и сжатии. Это свойство называют физической линейностью.
Стержневые модели, характеризующиеся геометрической и физической линейностью, называют линейными системами. Линейные системы обладают следующими свойствами.
| а) |
1. Внутренние усилия, напряжения и перемещения в любом сечении системы линейно зависит от значения приложенной нагрузки F,т. е. 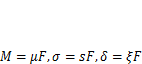 .Здесь µ, s,
.Здесь µ, s,  — коэффициенты пропорциональности для изгибающих моментов, напряжений и перемещений.
— коэффициенты пропорциональности для изгибающих моментов, напряжений и перемещений.
2. К линейным системам применим принцип независимости действия сил (принцип суперпозиций). Это значит, что внутренние усилия, напряжения или перемещения от одновременного действия нескольких нагрузок  (сил, моментов) равны сумме этих факторов, найденных от каждой из нагрузок, например,
(сил, моментов) равны сумме этих факторов, найденных от каждой из нагрузок, например,
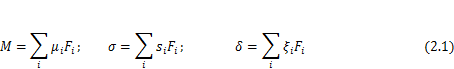
3. После разгрузки линейной системы (при F= 0) все ее точки возвращаются в исходное состояние (= 0), т. е. остаточные деформации равны нулю.
В необходимых случаях могут быть выполнены уточненные расчеты без указанных допущений. Как правило, они реализуются с помощью МКЭ (п. 4.5). В этих случаях, например, могут быть учтены упругопластические свойства материала (п. 1.5.3). В некоторых видах конструкций в целях снижения их массы используют стержни из высокопрочных материалов, имеющие пониженную жесткость, или гибкие оттяжки. Такие конструкции приходится рассчитывать с помощью нелинейных моделей по деформированной схеме (п. 9.2.2). В данном разделе рассматриваются методы расчета линейных стержневых систем.
Статическое и динамическое нагружение конструкции. Статическим называют такое нагружение, при котором упругие перемещения конструкции происходят настолько медленно, что возникающими при этом инерционными силами можно пренебречь. В противном случае нагружение считается динамическим, и при расчете внутренних усилий следует учитывать инерционные нагрузки (гл. 5).
