Согласно закону Ома для некоторого участка цепи, сила тока на участке цепи прямо пропорциональна напряжению на концах участка и обратно пропорциональна сопротивлению.

Закон Ома.

Согласно закону Ома для некоторого участка цепи, сила тока на участке цепи прямо пропорциональна напряжению на концах участка и обратно пропорциональна сопротивлению.

I = U/ R

Где U – напряжение концов участка,I– сила тока, R– сопротивление проводника.

U = I*R

R = U / I

Эти формулы справедливы лишь когда сеть испытывает на себе одно сопротивление.

Условием движения электрических зарядов в проводнике является наличие в нем электрического поля, которое создается и поддерживается особыми устройствами, получившими название источников тока.

Основной величиной, характеризующей источник тока, является его электродвижущая сила.

Электродвижущей силой источника (сокращенно ЭДС) называется скалярная физическая величина, характеризующая работу сторонних сил, способных создавать на зажимах источника (полюсах) разность потенциалов.

Она равна работе сторонних сил по перемещению заряженной частицы с положительным единичным зарядом от одного полюса источника к другому, т.е.

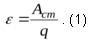
В СИ ЭДС измеряется в вольтах (В), т.е. в тех же единицах, что и напряжение.

Сторонние силы источника – это силы, которые осуществляют разделение зарядов в источнике и тем самым создают на его полюсах разность потенциалов. Эти силы могут иметь различную природу, но только не электрическую (отсюда и название) - Механические силы, химическая среда в аккумуляторе; световой поток в фотоэлементах.

Направление ЭДС — это направление принудительного движения положительных зарядов внутри генератора от минуса к плюсу под действием иной, чем электрическая, природы.

Внутреннее сопротивление генератора это сопротивление конструктивных элементов внутри него.

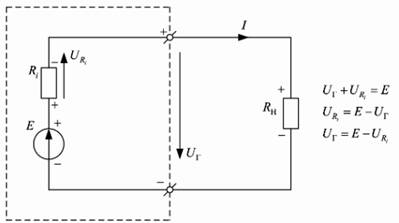
Если электрическую цепь разделить на два участка – внешний, с сопротивлением R, и внутренний, с сопротивлением r, то ЭДС источника тока окажется равной сумме напряжений на внешнем и внутреннем участках цепи:

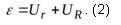
По закону Ома напряжение на любом участке цепи определяется величиной протекающего тока и его сопротивлением:

.

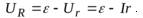Так как 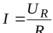, следовательно

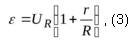, (3)

т.е. напряжение на полюсах источника при замкнутой цепи зависит от соотношения сопротивлений внутреннего и внешнего участков цепи. Если 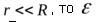приблизительно равно U.

Электрическое сопротивление.

Свойство материала проводника препятствовать прохождению через него электрического тока называется электрическим сопротивлением.

Из закона Ома: R = U / I

За единицу электрического сопротивления принят 1Ом.

Сопротивлением 1 Ом обладает проводник, в котором при напряжении 1 В проходит ток 1 А.

Величина, обратная сопротивлению, называется электрической проводимостью:

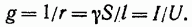
Единицей проводимости является сименс:

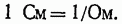
Величина, обратная удельной проводимости, называется удельным сопротивлением р, т. е.

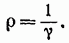
Увеличение температуры сопровождается усилением хаотического теплового движения частиц вещества, что приводит к увеличению числа столкновений электронов с ними и затрудняет упорядоченное движение электронов.

Сопротивление – резистор.

.

Метод узловых потенциалов.

Пример 2.7.4.

Определить значения и направления токов в ветвях методом узловых потенциалов для цепи рис. 2.7.4, если:

Е1=108 В; Е2=90 В; Ri1=2 Ом; Ri2=1 Ом; R1=28 Ом; R2=39 Ом; R3=60 Ом.

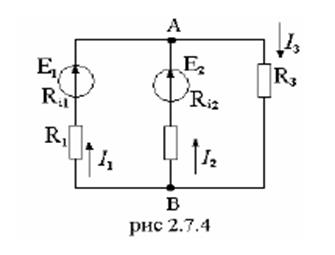
Решение.

Определяем токи в ветвях.

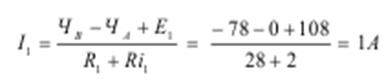
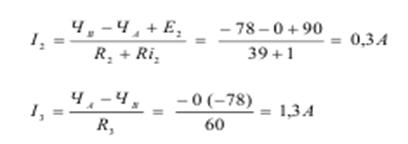
Метод двух узлов.

Одним из распространенных методов расчета электрических цепей является метод двух узлов.Этот метод применяется в случае, когда в цепи всего два узла

Метод контурных токов.

Алгоритм действий таков:

По второму закону Кирхгофа, относительно контурных токов, составляем уравнения для всех независимых контуров. При записи равенства считать, что направление обхода контура, для которого составляется уравнение, совпадает с направлением контурного тока данного контура. Следует учитывать и тот факт, что в смежных ветвях, принадлежащих двум контурам, протекают два контурных тока. Падение напряжения на потребителях в таких ветвях надо брать от каждого тока в отдельности.

Произвольно задаемся направлением реальных токов всех ветвей и обозначаем их. Маркировать реальные токи надо таким образом, чтобы не путать с контурными. Для нумерации реальных токов можно использовать одиночные арабские цифры (I1, I2, I3 и т. д.).

При алгебраическом суммировании без изменения знака берется контурный ток, направление которого совпадает с принятым направлением реального тока ветви. В противном случае контурный ток умножается на минус единицу.

Пример расчёта сложной цепи методом контурных токов.

В цепи, изображённой на рисунке 1, рассчитать все токи методом контурных токов. Параметры цепи: Е1 = 24 В, Е2 = 12 В, r1 = r2 = 4 Ом, r3 = 1 Ом, r4 = 3 Ом.

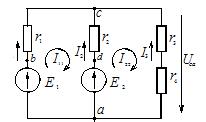
Рис. 1. Схема электрической цепи для примера расчета по методу контурных токов

Решение. Для расчета сложной цепи этим методом достаточно составить два уравнения, по числу независимых контуров. Контурные токи направляем по часовой стрелке и обозначаем I11 и I22 (см. рисунок 1).

По второму закону Кирхгофа относительно контурных токов составляем уравнения:

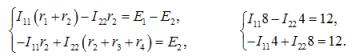
Решаем систему и получаем контурные токи I11 = I22 = 3 А.

Следует отметить, как положительный факт, что в методе контурных токов по сравнению с решением по законам Кирхгофа приходится решать систему уравнений меньшего порядка. Однако этот метод не позволяет сразу определять реальные токи ветвей.

Закон Ома.

Согласно закону Ома для некоторого участка цепи, сила тока на участке цепи прямо пропорциональна напряжению на концах участка и обратно пропорциональна сопротивлению.

I = U/ R