Теорема Эйлера-Даламбера. Мгновенная ось вращения. Мгновенные угловая скорость и угловое ускорение.

Теорема: твёрдое тело имеющее одну неподвижную точку можно переместить из одного положения в другое поворотом вокруг некоторой оси проходящей через эту точку. В соответствии с теоремой Эйлера-Даламбера вращение тел при сферическом движении происходит вокруг некоторой оси которая постоянно меняет своё положение (мгновенная ось вращения). Вектор угловой скорости ω всегда направлен вдоль мгновенной оси и в процессе движения постоянно меняет своё положение.

Мгновенная угловая скорость определяется как производная от угловой координаты 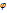от времени t. ω=d 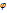/dt

Мгновенное угловое ускорение определяется как производная от угловой скорости по времени

έ=dω/dt

Вопрос 21. Скорость точек тела при сферическом движении. Формулы Эйлера. Определение ускорений точек тела при сферическом движении.

Скорости точек тела определяются по формулам Эйлера

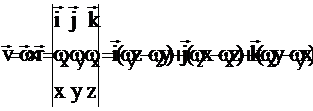
w_x,w_y,w_z – проекции вектора угловой скорости. Проекция вращательной (окружной) скорости: v_x=w_yz – w_zy; v_y=w_zx – w_xz; v_z=w_xy – w_yx. Если ось вращения совпадает с осью z, то v_x= – wy; v_y=wx. Ускорение: .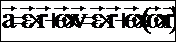

Вращательное ускорение 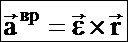, модуль вращат. уск. а^вр=e×r×sina, направлено по касательной к траектории точки, т.е. параллельно скорости. Центростремительное (осестремительное) ускорение 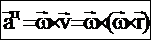, а^ц=w²×R, направлено по радиусу к оси (центру) вращения. Модуль полного уск.: 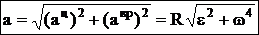. Угол, между векторами полного и центростремит-ного ускорений: .

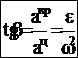Вектор скорости точки направлен перпендикулярно плоскости векторов ω и r таким образом чтобы смотря ему навстречу поворот на наименьший угол от ω к Vr был виден против часовой стрелки.

Вопрос 22. Общий случай движения свободного твёрдого тела. Уравнения движения свободного твёрдого тела. Скорости точек тела.

Движение свободного тв.тела(общий случай движения). Свободное тв.тело имеет шесть степеней свободы. При рассмотрении движения св.тв.тела, кроме неподвижной системы координат Oxyz, вводится подвижная система координат Ax₁y₁z₁, которая связана с телом в точке А. Тогда движ. св.тв.тела представляет собой сложное движение, которое можно рассматривать как состоящее из поступательного движения вместе с полюсом (А) и сферич. движ. вокруг полюса. Ур-ия движ.св.тв.тела: x_A=f₁(t); y_A=f₂(t); z_A=f₃(t); Y=f₄(t); q=f₅(t); j=f₆(t) (углы Эйлера). Первые три ур-ия определяют поступательную часть движ. и зависят от выбора полюса, остальные три определяют сферич. движ. вокруг полюса и от выбора полюса не зависят. Скорость любой точки св.тв.тела = геометрической сумме скорости полюса и скорости этой точки в ее сферическом движении вокруг полюса.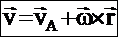

Вопрос 23. Сложное движение точки. Абсолютное, относительное и переносное движения. Абсолютные, относительные и переносные скорость и ускорение точки. Основное векторное уравнение кинематики сложного движения.

Сложным называется такое движение тела при котором оно одновременно участвует в двух или нескольких движениях. В рассмотрение вводится подвижная и неподвижная система отсчёта аналогично сложному движению тела. Сложное движение тела рассматривается как совокупность двух движений – относительного и переносного.В этом случае вводится подвижная система координат (Oxyz), которая совершает заданное движение относительно неподвижной (основной) системы координат (O₁x₁y₁z₁). Абсолютным движением точки назыв. движение по отношению к неподвижной системе координат. Относительное движение – движение по отношению к подвижной системе коорд. (движение по вагону). Переносное движение – движение подвижной сист. координат относительно неподвижной (движение вагона).