Открытая транспортная задача

Транспортная задача называется открытой, если запасы груза превышают потребности в нем или, если потребности невозможно удовлетворить имеющимися запасами. Для решения задачи в этих случаях вводят фиктивного потребителя или поставщика груза. На этих (реально не существующих) участников перевозок и записывают недостающее количество груза или потребности в нем. Стоимости перевозок от фиктивных станций полагаются равными нулю. Тогда задача становится закрытой и решается методом потенциалов. Для примера, ниже приведена задача, в которой введен фиктивный потребитель В₅, позволяющий вывезти все грузы из пунктов А₁, А₂, А₃.

	В1	В2	В3	В4	В5 *
А1	10				40*
А2	15		35
А3	5	40		25

В этом примере построен опорный план по методу наименьшей стоимости. Фиктивный потребитель и перевозка равная грузу, который фактически остается на станции А₁, помечены звездочкой. Задача, записанная в таблице, является закрытой и ее решение можно довести до получения оптимального плана (предлагаем Вам сделать это самостоятельно).

6.6. Проблема вырожденного плана задачи

При определении первого опорного плана нередко возникает ситуация, когда число занятых клеток меньше величины m+n-1. В этом случае система (6.5) не позволяет определить потенциалы потребителей и поставщиков. Решение проблемы рассмотрим на примере. При построении опорного плана методом северо-западного угла в клетку А₁-В₁ была внесена перевозка x₁₁ = 50, при этом, первая строка и первый столбец были вычеркнуты одновременно (что и привело к вырожденности плана). Такую клетку следует запомнить или отметить с тем, чтобы после заполнения всей таблицы ввести фиктивную перевозку в вычеркнутую строку или столбец, выбрав клетку с наименьшей стоимостью. В примере это клетка А₁-В₃, которая в дальнейших расчетах считается занятой с перевозкой равной нулю.

	В1	В2	В3	В4	В5
А1
А2
А3

Вырожденность плана также может возникнуть при пересчете свободной клетки, если в четных вершинах цикла стоят равные по величине перевозки, совпадающие с величиной сдвига по циклу 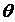. В таком случае следует внести фиктивную перевозку равную 0 в ту из освобождающихся клеток, в которой стоимость меньше.

ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ

На станциях А_i (i = 1, 2, 3) сосредоточен однородный груз в количестве а_i единиц груза, который требуется перевезти на станции назначения В_j (j = 1,.. 5) в соответствии с потребностями каждой станции в b_j единиц груза. Известны затраты 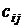на перевозку единицы груза с любой станции A_i на любую станцию B_j.

Требуется составить такой план перевозок, чтобы весь груз был вывезен, все потребности были бы удовлетворены, а суммарные затраты были бы минимальны. Исходные данные приведены в таблицах 1 и 2.

Табл.1. Запасы и потребности на станциях участниках процесса перевозок.

Вариант	Запасы	Потребности
А1	А2	А3	В1	В2	В3	В4	В5

Табл.2. стоимости перевозки единицы груза.

Вариант

c11

c12

c13

c14

c15

c21

c22

c23

c24

c25

c31

c32

c33

c34

c35

ЗАДАЧА ОБ ОПТИМАЛЬНОМ НАЗНАЧЕНИИ

Постановка задачи

Пусть имеется nработ, которые могут выполнить n исполнителей. Известны затраты 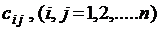при назначении i-го исполнителя на j-ую работу.

Требуется так распределить исполнителей по работам, чтобы все работы выполнялись, все исполнители были заняты и суммарные затраты при производстве работ были минимальны. Предполагается, что каждый исполнитель выполняет одну работу и каждая работа будет поручена одному исполнителю.

Математическая модель

Обозначим назначение i-го исполнителя на j-ую работу, как 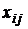. Тогда

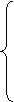
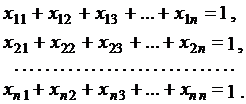(7.1)

С другой стороны, каждая работа будет поручена одному исполнителю. При этом выполняется условие неотрицательности:

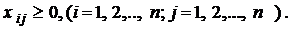
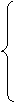
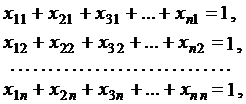(7.2)

Кроме того:

x_ij =

Функция цели задачи по критерию минимума суммарных затрат:

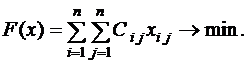
Очевидно, что данная задача сводится к транспортной задаче, если запасы и потребности равны единице. Как правило, число исполнителей равно числу работ, то есть это закрытая задача. Если это условие не выполняется, то вводят либо фиктивного исполнителя, либо фиктивную работу, в результате задача становится закрытой, а в полученном оптимальном назначении одна работа не будет выполнена, либо один исполнитель будет простаивать. Запишем данные задачи в таблицу:

	B1	B2	B3	…	Bn	Запасы
А1	c11 x11	c12 x12	c13 x13	…	c1n x1n
А2	c21 x21	c22 x22	c23 x23	…	c2n x2n
…	…	…	…	…	…	…
Аn	cn1 xn1	cn2 xn2	cn3 xn3	…	cnn xnn
Потребности

Здесь А₁, А₂, …, А_n – работы, В₁, В₂, …, В_n – исполнители.

Так как «запасы» и «потребности» всегда равны 1, то при решении их не принято писать, кроме того величины «перевозок» также равны 1, поэтому занятые клетки можно просто помечать каким-либо образом.

Рассмотрим пример задачи о назначениях размерности n = 5. Здесь приведен первый опорный план, построенный по методу северо-западного угла:

	В1	В2	В3	В4	В5
А1	(1)
А2		(1)
А3			(1)
А4				(1)
А5					(1)

Из таблицы видно, что план вырожден n-1 раз. Такой особенностью обладают все планы задачи об оптимальном назначении. В результате этого стандартные методы решения транспортной задачи неэффективны и, кроме того, часто приводят к зацикливанию. Рассмотрим «венгерский метод» решения задачи.