Двойственность в задачах линейного программирования
Построение двойственных моделей
Двойственная задача – это вспомогательная задача ЛП, формулируемая с помощью определенного правила непосредственно из условия исходной задачи. Заметим, что для разных моделей исходной задачи правила построения двойственных моделей отличаются.
Рассмотрим правило построения двойственной модели, если исходная задача задана в виде стандартной модели:
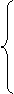
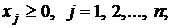
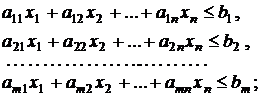 (3.1)
(3.1)
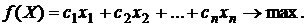 (3.2)
(3.2)
Правило построения двойственной модели:
1. Надо проверить, отвечает ли исходная модель двум требованиям:
а) все неравенства в системе (3.1) имеют одинаковый знак « £ » или (« ³ »).
б) если целевая функция ЗЛП максимизируется, то знак в неравенствах должен быть «£», а если целевая функция минимизируется, то знак должен быть «³». В нашей модели это требование выполнено.
2. Каждому i-тому ограничению исходной задачи соответствует j-тое неизвестное в двойственной задаче: так, неравенству 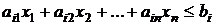 соответствует
соответствует 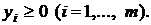
3. Каждому неизвестному исходной модели соответствует ограничение двойственной модели. Матрица коэффициентов при неизвестных двойственной задачи является транспонированной матрицей исходной задачи. Неравенства ограничения имеют противоположный смысл неравенствам исходной задачи. Правые части ограничений равны коэффициентам функции цели прямой задачи. Таким образом, для i-ой переменной получим
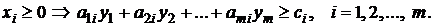
4. Целевая функция двойственной модели имеет вид:
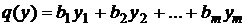 ,
,
и решается задача минимизации. Запишем модели по соответствию:
 |  | ||||||||||
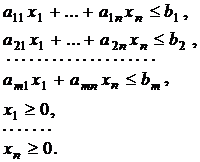 | |||||||||||
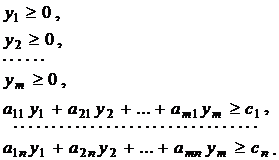 | |||||||||||
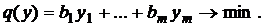 | |||||||||||
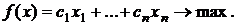 | |||||||||||
Такие модели задачи ЛП называются симметричными. Заметим, что для полученной двойственной модели можно также построить по тем же првилам двойственную модель, которая будет представлять исходную модель ЗЛП.
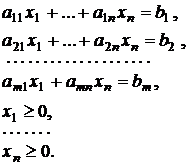 | 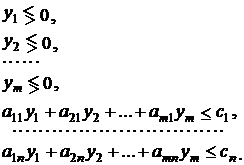 |
 В случае если исходная задача ЛП − основная задача минимизации, то двойственная ей - стандартная задача максимизации. Пара таких задач имеет вид:
В случае если исходная задача ЛП − основная задача минимизации, то двойственная ей - стандартная задача максимизации. Пара таких задач имеет вид: 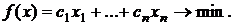 | 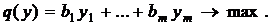 |
при этом переменные второй задачи 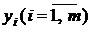 могут иметь любой знак.
могут иметь любой знак.
Для двойственных задач справедливы следующие теоремы двойственности.
Теоремы двойственности
Теорема 1. Если X – любое опорное решение исходной задачи, а Y – любое опорное решение соответствующей ей двойственной задачи, то 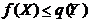 .
.
Теорема 2. Если одна из взаимно двойственных задач имеет оптимальное решение, то и другая тоже имеет оптимальное решение, причем оптимальные значения целевых функций равны между собой 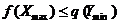 .
.
Теорема 3.Если одна из взаимодвойственных моделей не имеет оптимального решения (например, целевая функция неограниченна), то и другая не имеет допустимых решений, то есть система ограничений в ней – несовместна.
Теорема 4. Пусть одна из взаимно двойственных задач имеет оптимальное решение. Тогда для неизвестных и ограничений выполняются следующие условия:
1) если координата хjоптимальногоплана исходной модели строго положительна, то соответствующее ограничение выполняется при подстановке в него координат оптимального решения, как уравнение;
2) если при подстановке Xопт вкакое-либо ограничениеисходной задачи оно выполняется как строгое неравенство, то соответствующая ему переменная уi равна нулю.
Теорема 5.Для того, чтобы два допустимых решения Х* и Y* пары двойственных задач были оптимальными решениями, необходимо и достаточно, чтобы они удовлетворяли системе уравнений:
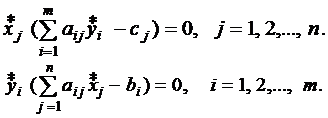
Зная оптимальное решение одной из двойственных задач, можно, используя теоремы двойственности, найти оптимальное решение другой. Рассмотрим пример.
Пример. Вернемся к задаче, решение которой мы получили в п.2. Построим для заданной модели двойственную и решим ее с помощью теорем двойственности:
 12x1+4x2 ≤ 300, y1 ≥ 0,
12x1+4x2 ≤ 300, y1 ≥ 0,
4x1+4x2 ≤ 120, y2 ≥ 0,
3x1+12x2 ≤ 252, y3 ≥ 0,
x1 ≥ 0,12y1 +4y2+3y3 ≥ 30,
x2 ≥ 0,4y1+4y2+12y3 ≥ 40,
f(x) =30x1 + 40 x2 → max. q(y) =300 y1 + 120y2 + 252y3 →min.
Двойственная модель задача ЛП построена по правилу, изложенному ранее.
Нам известно, что исходная задача имеет оптимальное решение:
Xmax = (12, 18), fmax= f (Xmax) = 1080.
Воспользуемся первой теоремой двойственности. Двойственная модель тоже имеет оптимальное решение, причем оптимальное значение целевой функции q(y)тоже равно 1080, то есть q(Ymin) = 1080.
Далее, будем использовать теорему 4. Начнем с 1-ой части:
x1 = 12 > 0 Þ 12y1+4y2+3y3 = 30,
x2 = 18 > 0 Þ 4y1+4y2+12y3 = 40.
Подставим оптимальное решение xmax в ограничения задачи:
144 + 72 = 216 < 300 Þ у1 = 0,
48 + 72 = 120 = 120 Þ у2 > 0,
36 + 216 = 252 = 252 Þ у3 > 0.
Получим систему уравнений для определения оптимального решения двойственной модели:
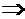
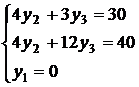
Получим: 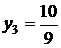 ,
, 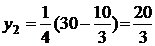 ,
, 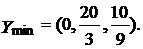
Проверим расчет: 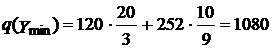 .
.
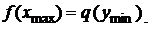 Задача решена.
Задача решена.
