Тест для самопроверки знаний
По Теме 1. Матрицы и определители
1. Для умножения матрицы любого размера на число достаточно:
· умножить на это число элементы любой строки этой матрицы 
· умножить на это число элементы любого столбца этой матрицы 
· умножить на это число все без исключения элементы этой матрицы 
2. Для какой из приведенных пар матриц определена операция умножения?
· 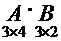

· 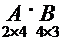

· 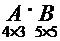

3. Минором Mij элемента aij квадратной матрицы A n-го порядка называется:
· любой определитель (n-1)-го порядка, полученный из этой матрицы 
· любой определитель второго порядка, полученный из этой матрицы 
· определитель, полученный вычеркиванием i-ой строки и j-го столбца этой матрицы 
4. Алгебраическим дополнением Aij элемента aij квадратной матрицы A называется:
· минор этого элемента, взятый со знаком (- 1)i+j 
· минор элемента aij 
· любой определитель (n–1)-го порядка матрицы A 
5. Вырожденной называется квадратная матрица, определитель которой:
· не равен нулю 
· равен нулю 
· равен единице 
6. Для существования обратной матрицы для матрицы A необходимо и достаточно, чтобы матрица A была:
· невырожденной 
· вырожденной 
· единичной 
7. Какая из перечисленных ниже операций приводит к изменению ранга матрицы?
· перестановка строк (столбцов) матрицы 
· транспонирование матриц 
· вычеркивание любой строки (столбца) матрицы 
ТЕМА 2. Системы линейных уравнений
2.1. Основные понятия и определения
В самом общем случае система m линейных уравнений с n неизвестными имеет следующий вид:
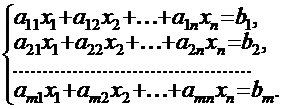
где 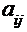 и
и 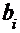 при всех
при всех 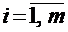 и
и 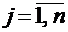 есть произвольные числа, называемые, соответственно, коэффициентами при неизвестных и свободными членами уравнений системы.
есть произвольные числа, называемые, соответственно, коэффициентами при неизвестных и свободными членами уравнений системы.
Решением системы уравнений называется такая совокупность чисел, при подстановке которой в каждое из уравнений системы последнее обращается в числовое тождество.
Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной,если она решений не имеет.
В свою очередь, совместная система уравнений называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.
Две системы уравнений называются равносильнымиили эквивалентными, если они имеют одно и то же множество решений.
Всякая система уравнений, состоящая из m уравнений с n неизвестными, всегда может быть записана в матричной форме:
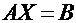 ,
,
где A – матрица коэффициентов при неизвестных, в общем случае прямоугольная размером m ´ n, X – матрица-столбец неизвестных размера n ´ 1, B – матрица-столбец свободных членов размера m ´ 1.
Решение систем линейных уравнений
Метод обратной матрицы
Если в системе линейных уравнений число уравнений равно числу неизвестных и матрица системы А является невырожденной, т.е. |А| ≠ 0, то для матрицы системы существует обратная матрица А-1.
Запишем такую систему в матричном виде: AX = B. Умножая слева обе части этого матричного равенства на матрицу А-1, получим: A-1(AX) = A-1B. Так как (A-1A)X = EX = X, то решением системы будет матрица-столбец:
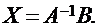
ПРИМЕР: Для системы уравнений:
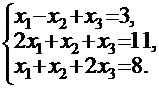
определитель матрицы системы |А| = 5 ≠ 0 (убедитесь в этом сами). Следовательно, обратная матрица для матрицы А существует и имеет вид:
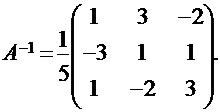
Поэтому решением данной системы будет матрица-столбец:
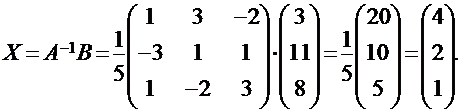
Правило Крамера
Предположим, что матрица системы А является квадратной, а ее определитель Δ0 = |А| ≠ 0. Тогда единственное решение системы может быть найдено по формулам Крамера:
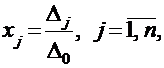
где Δj – определитель матрицы, полученной из матрицы системы заменой j –го столбца на столбец свободных членов.
ПРИМЕР: Решим с использованием формул Крамера систему примера в подразделе 2.2.1. Здесь Δ0 = |А| = 5,
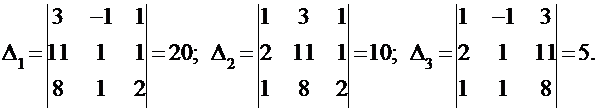
И по формулам Крамера получим:

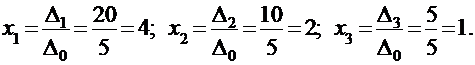
Метод Гаусса
Методы, рассмотренные в предыдущих подразделах, применимы только когда число уравнений равно числу неизвестных. Однако существует универсальный метод решения таких систем, применимый при любом соотношении между числом уравнений и числом неизвестных – метод Гаусса.
Для любой системы линейных уравнений можно составить расширенную матрицу системы, которая отличается от матрицы системы тем, что справа добавляется еще один столбец – столбец свободных членов, который для удобства принято отделять вертикальной чертой. В общем случае расширенная матрица системы имеет вид:

Метод Гаусса заключается в том, что с помощью элементарных преобразований строк расширенная матрица системы приводится к ступенчатому виду. Система линейных уравнений, соответствующая этой матрице, будет эквивалентна исходной системе. Для системы уравнений, составленной по ступенчатой матрице, все решения могут быть найдены последовательно, начиная с последнего уравнения.
