ТЕОРЕТИКО – ПРАКТИЧЕСКИЙ КУРС

ТЕОРЕТИКО – ПРАКТИЧЕСКИЙ КУРС

«ОСНОВЫ ЛИНЕЙНОЙ АЛГЕБРЫ

ДЛЯ ЭКОНОМИСТОВ И МЕНЕДЖЕРОВ»

Учебное пособие по курсу «Линейная алгебра»

Москва

Рекомендовано к изданию

Решением Ученого совета ИМЭС

(Протокол № 9 от 26 мая 2016 г.)

Настоящее учебное пособие разработал кандидат физико-математических наук, доцент, заведующий кафедрой математики и информатики ИМЭС Налимов Валерий Николаевич.

ПРЕДИСЛОВИЕ

Настоящее учебное пособие предназначено для студентов первого курса заочной формы обучения и по тематическому объему полностью соответствует требованиям рабочих программ учебной дисциплины «Линейная алгебра», которые, в свою очередь, полностью соответствуют требованиям действующих федеральных государствен­ных образовательных стандартов по направлениям 38.03.01 “Экономика” и 38.03.02 “Менеджмент”.

Порядок изложения разделов, тем и основных подразделов тем в данном учебном пособии соответствует порядку, принятому в рабочих программах учебной дисциплины «Линейная алгебра» по соответствующему направлению подготовки. Однако нумерация тем и подразделов в настоящем пособии может отличаться от нумерации, принятой в учебном пособии [1].

По каждой теме и подразделу темы данное пособие содержит теоретический материал, изложенный в предельно сжатой форме (теоремы и аксиомы, математические факты, формулы и их следствия, имеющие практическую значимость), а также примеры использования этого материала для решения задач. В конце изложения теоретического материала каждой темы приведены вопросы для самопроверки знаний по этой теме курса. Некоторые темы курса заканчиваются вопросами в форме тестов.

После ознакомления с теоретическим материалом студенту следует кратко и четко ответить на вопросы, самостоятельно оценив и отобрав материал, изложенный в литературе, ссылки на которую приведены в конце каждой темы, или подраздела, а полный список литературы приводится в конце пособия. Ваши ответы должны быть размещены непосредственно в Вашем экземпляре пособия. Причем при тестовом варианте ответов на вопросы Вы должны поставить любой значок (крестик, галочку и т.п.) только в одном квадрате, соответствующем верному, на Ваш взгляд, ответу на поставленный вопрос.

Настоящее пособие может быть полезно и студентам 1 курса очно-заочного (вечернего), а также очного (дневного), отделений ИМЭС, при подготовке к сдаче экзаменов по дисциплине «Линейная алгебра».

ЛИСТ СТУДЕНТА

Фамилия ___________________________________

Имя ________________________________________

Отчество ____________________________________

Факультет ___________________________________

Курс _________________________________________

Группа _______________________________________

Дата начала работы: «_____» _____________ 20___ г.

Дата окончания работы «_____» ______________ 20___ г.

Личная подпись _________________________

ЛИСТ РЕЦЕНЗИИ

Рецензент ______________________

______________________

«_____» _______________ 20____ г.

ТЕМА 1. Матрицы и определители

Основные свойства определителей

1. При однократной перестановке двух строк (или столбцов) опреде­литель меняет свой знак.

2. Умножение всех элементов какой-либо строки (или столбца) опре­делителя на одно и то же число равносильно умножению всего оп­ределителя на это же число.

3. Если некоторая строка (или столбец) определителя целиком состоит из нулей, то этот определитель равен нулю.

4. Если элементы какой-либо строки (или столбца) определителя про­порциональны (в частном случае равны) соответствующим элемен­там другой строки (или столбца), то этот определитель равен нулю.

5. При транспонировании матрицы ее определитель не меняет своего значения, т.е. |А^Т| = |А|.

6. Определитель не изменится, если к элементам какой-либо строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на любой множитель.

7. Определители верхней треугольной, нижней треугольной и диаго­нальной матриц равны произведению элементов их главной диаго­нали.

8. Определитель произведения двух квадратных матриц равен произ­ведению их определителей: |АВ| = |А|∙|В|, откуда следует: |АВ| = |ВА|.

Обратная матрица и обращение матриц

Определение.Матрица А^-1 называется обратной для квадратной матрицы А, если выполняется равенство:

А-1∙А = А∙А-1 = Е.

Определение. Если определитель квадратной матрицы отличен от нуля, то такая матрица называется невырожденной. Если же определитель матрицы равен нулю, то такая матрица называется вырожденной.

Обратная матрица А-1 существует и единственна тогда и только тогда, когда исходная матрица А является невырожденной.

Алгоритм обращения матрицы

1. Вычислить определитель матрицы А. При этом обратная матрица будет существовать, только в случае |А| ≠ 0.

2. Транспонировать матрицу А, т.е. найти матрицу А^Т.

3. Найти алгебраические дополнения всех элементов матрицы А^Т и, расставив их на места соответствующих элементов, получить присоединенную к А матрицу .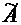

4. Найти матрицу обратную матрице А по формуле: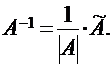

5. Проверить правильность вычислений, убедившись в справедли­вости любого из равенств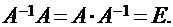

ПРИМЕР: Найти матрицу, обратную матрице

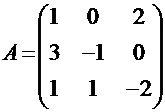
1. Находим |А| = 10 ≠ 0, следовательно, матрица, обратная к матрице А существует.

2. Транспонируем матрицу А и найдем:

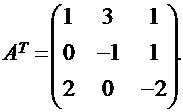
3. Последовательно найдем алгебраические дополнения всех элементов матрицы А^Т и, расставив их на места элементов в матрице А^Т, получим присоединенную к матрице А матрицу в виде:

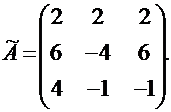
4. Находим искомую матрицу:

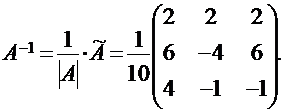
5. Проверка показывает, что вычисления проведены правильно:

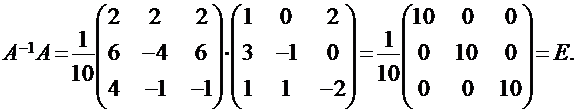
Алгоритм Гаусса (пошаговый)

Шаг 1. Если элемент а₁₁ исходной матрицы равен нулю, т.е. а₁₁= 0, то перестановкой строк или столбцов матрицы добиваются того, чтобы элемент а₁₁ полученной матрицы был отличен от нуля.

Шаг 2. Сложением первой строки (в ней а₁₁ ≠ 0), умноженной на под­ходящие (различные для различных строк) множители, с другими строками до­биваются того, чтобы все элементы первого столбца матрицы, стоящие ниже элемента а₁₁ ≠ 0, т.е. элементы а₂₁, а₃₁, … были бы равны нулю.

Шаг 3. Теперь, либо уже получена ступенчатая матрица, либо в строках со второй по m-ую имеется по крайней мере один ненулевой элемент, который при помощи перестановки строк или столбцов (кроме первой строки и первого столбца) может быть поставлен на второе по порядку место в главной диагона­ли, т.е. на место элемента а₂₂. После этого снова выполняют операции, аналогичные шагу 2, но сложе­ние осуществляют уже со второй строкой, и в результате получают, что все эле­менты второго столбца, стоящие ниже элемента а₂₂ равны нулю и т.д. и т.д.

Аналогичные перечисленным операции применяются и к последующим строкам матрицы, а сам процесс продолжают до тех пор, пока не получат иско­мую, ступенчатую матрицу. Если в процессе выполнения таких операций на каком-то шаге получается нулевая строка, то ее вычеркивают.

ПРИМЕР: Найти ранг матрицы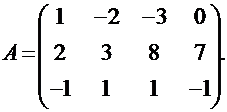

Решение. Убедившись, что для данной матрицы элемент а₁₁ = 1 ≠ 0, сразу переходим к шагу 2. Умножив первую строку матрицы на число (- 2), сло­жив ее со второй строкой и записав результат во вторую строку, а также сложив первую строку матрицы с третьей строкой и записав результат в третью строку, получим матрицу вида:

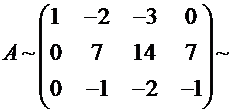
Убедившись, что в полученной после 2 шага матрице элемент а₂₂ = 7 ≠ 0, переходим к реализации шага 3, для чего умножим вторую строку этой матрицы на число 1/7 и сложим ее с третьей строкой, в результате полу­чим:

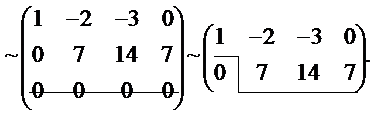
У полученной ступенчатой матрицы третья, нулевая строка может быть вычеркнута без изменения ранга этой матрицы. Оставшаяся матрица имеет раз­мер 2 ´ 4 и также является ступенчатой. Очевидно, что полученная ступенчатая матрица имеет две ступеньки (две строки), а, следовательно, ранг ее равен 2 и, следовательно, ранг исходной матрицы также равен 2.

Рекомендуемая литература по теме 1:[1 – 3].

Метод обратной матрицы

Если в системе линейных уравнений число уравнений равно числу неизвестных и матрица системы А является невырожденной, т.е. |А| ≠ 0, то для матрицы системы существует обратная матрица А^-1.

Запишем такую систему в матричном виде: AX = B. Умножая слева обе части этого матричного равенства на матрицу А^-1, получим: A^-1(AX) = A^-1B. Так как (A^-1A)X = EX = X, то решением системы будет матрица-столбец:

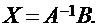
ПРИМЕР: Для системы уравнений:

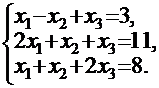
определитель матрицы системы |А| = 5 ≠ 0 (убедитесь в этом сами). Следовательно, обратная матрица для матрицы А существует и имеет вид:

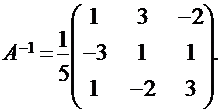
Поэтому решением данной системы будет матрица-столбец:

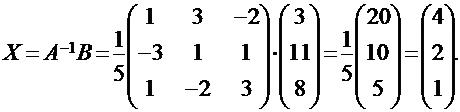
Правило Крамера

Предположим, что матрица системы А является квадратной, а ее определитель Δ₀ = |А| ≠ 0. Тогда единственное решение системы может быть найдено по формулам Крамера:

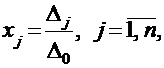
где Δ_j – определитель матрицы, полученной из матрицы системы заменой j –го столбца на столбец свободных членов.

ПРИМЕР: Решим с использованием формул Крамера систему примера в подразделе 2.2.1. Здесь Δ₀ = |А| = 5,

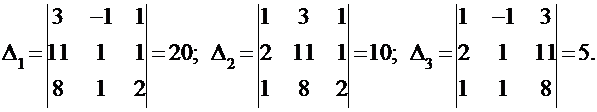
И по формулам Крамера получим:

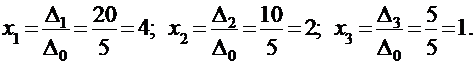
Метод Гаусса

Методы, рассмотренные в предыдущих подразделах, примени­мы только когда число уравнений равно числу неизвестных. Однако существует универсальный метод решения таких систем, применимый при любом соотношении между числом уравнений и числом неизвестных – метод Гаусса.

Для любой системы линейных уравнений можно составить расширенную матрицу системы, которая отличается от матрицы системы тем, что справа добавляется еще один столбец – столбец свободных членов, который для удобства принято отделять вертикальной чертой. В общем случае расширенная матрица системы имеет вид:

Метод Гаусса заключается в том, что с помощью элементар­ных преобразований строк расширенная матрица системы приводится к ступенчатому виду. Система линейных уравнений, соответствующая этой матрице, будет эквивалентна исходной системе. Для системы уравнений, составленной по ступенчатой матрице, все решения могут быть найдены последовательно, начиная с последнего уравнения.

Теорема Кронекера – Капелли

Система линейных уравнений совместна только тогда, когда ранг матрицы системы равен рангу расширенной матрицы системы.

ПРИМЕР: Проверьте совместность системы линейных уравнений:

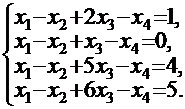
Для сравнения рангов матриц составим расширенную матрицу системы и приведем ее к ступенчатому виду:

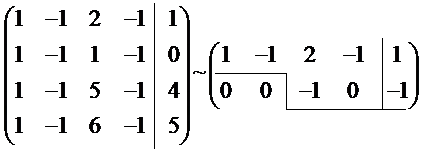
Рассматривая полученную ступенчатую матрицу, имеющую только две ступеньки, можно сделать вывод, что ранг матрицы системы равен рангу расширенной матрицы системы и равен 2. Согласно критерию, данная система уравнений – совместна.

Переход к новому базису

Пусть в пространстве R имеется два базиса: «старый» 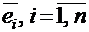и «новый» 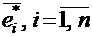. Очевидно, что каждый из векторов нового базиса можно представить в виде линейной комбинации векторов старого базиса:

(*)

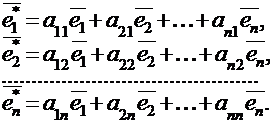Это же представление можно записать в матричной форме:

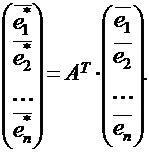
Полученная запись означает, что переход от старого базиса к новому задается матрицей перехода А. Эта матрица, как и матрица А^Т невырожденная, т.к. в противном случае ее строки (а, следовательно, и базис­ные векторы) оказались бы линейно зависимы.

Найдем зависимость между координатами одного и того же век­тора в разных базисах. Пусть некоторый вектор 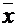имеет координаты 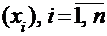относительно старого базиса и координаты 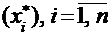относительно нового базиса, т.е. можно записать:

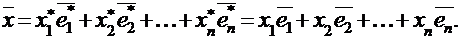
Если теперь подставить в среднюю часть этих равенств выражения для векторов 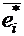из равенств (*), то после несложных преобразо­ва­ний можно получить:

(**)

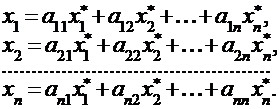Систему представлений (**) можно записать и в матричной форме, т.е. в виде: Х = А∙Х^*,именно так координаты вектора в старом базисе выра­жаются через координаты того же вектора в новом базисе.

Если решить систему уравнений (**) методом обратной матрицы (это можно сделать, т.к. матрица A невырожденная, и обратная ей матрица существу­ет), то получим: Х^* = А^-1Х именно таким образом координаты вектора в новом базисе выражаются через координаты того же вектора в старом базисе.

ПРИМЕР:Найдите координаты вектора 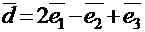в новом базисе примера подраздела 3.3.

Используя разложения векторов 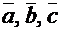по векторам базиса, приведенные в условии примера подраздела 3.3, можно матрицу перехода от старого базиса к новому записать в виде:

.

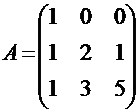Можно убедиться в том, что определитель этой матрицы |А| = 7 ≠ 0. Поэтому существует обратная ей матрица, которая имеет вид (убедитесь в этом самостоятельно):

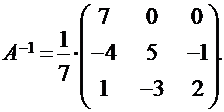
Для отыскания координат вектора 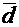в новом базисе 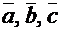воспользуемся формулой: Х^* = А^-1Х и найдем:

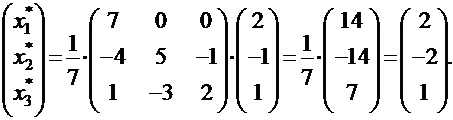
Таким образом разложение вектора по векторам нового базиса можно записать в виде: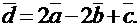

Евклидово пространство

Выше мы ввели понятие линейного векторного пространства, в котором определены операции сложения векторов и умножения их на число, а также ввели понятия размерности и базиса этого пространства. Теперь дополним это пространство метрикой, т.е. укажем способы измерения длин векторов и углов между ними. Это можно сделать, доопределив в векторном пространстве поня­тие скаляр­но­го произведения векторов, естественно, обобщив его на случай n-мерных век­торов.

Определение. Скалярным произведением двух векторов 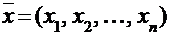и 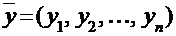называется число, равное:

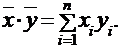
Отметим основные свойства скалярного произведения, которые непо­средственно вытекают из сформулированного определения.

1. 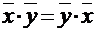- коммутативное свойство;

2. 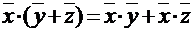- дистрибутивное свойство;

3. 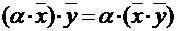- свойство справедливое для любого действительного α;

4. 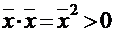, есл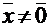и , и 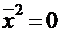, если .

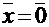Определение.Линейное векторное пространство, в котором опре­делено скалярное произведение векторов, удовлетворяющее указанным четырем свойствам, рассматриваемым как аксиомы, называется евклидовым про­странством.

Определение. Длинойили нормойвектора 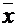в n-мерном евклидо­вом пространстве называется корень квадратный из его скалярного квадрата, т.е.:

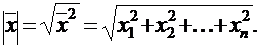
Определенная таким образом норма вектора обладает некоторыми свойствами, основное из которых записывается в виде: 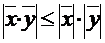и носит название неравенства Коши-Буняковского.

Очевидно, что косинус угла j между двумя векторам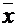и и 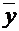можно определить равенством, непосредственно вытекающим из неравенства Коши-Бу­няковского:

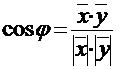, где: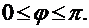

Определение.Два вектора называются ортогональными, если их скалярное произведение равно нулю.

Определение.Векторы 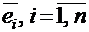n-мерного евклидова простран­ства Rⁿ образуют ортонормированный базис, если они попарно ортогональны, и норма каждого из них равна единице.

Существует теорема, устанавливающая одно из основных свойств евкли­дова пространства.

Во всяком n-мерном евклидовом пространстве существует ортонормированный базис.

Примером одного из таких ортонормированных базисов является сис­тема из n единичных векторов, у которых i-ая компонента равна 1, а все осталь­ные компоненты равны нулю, т.е. базис из векторов: 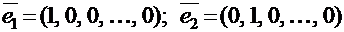и т.д.

Линейные операторы

Если задан закон (правило), по которому каждому вектору 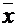пространства Rⁿ ставится в соответствие единственный вектор 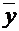этого же пространства, то говорят, что задан оператор (преобразование, отображение) 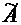и записывают .

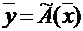Оператор 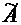называется линейным, если для любых векторов 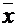и 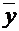пространства Rⁿ и любого действительного числа λ выполняются соотношения:

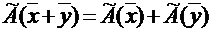· - свойство аддитивности оператора;

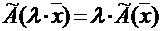· - свойство однородности оператора.

Опираясь на свойства линейности оператора, можно показать, что его воздействие на вектор 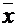состоит в том, что матрица-столбец координат этого вектора (в некотором базисе) умножается слева на квадратную матрицу А оператора и в результате получается матрица-столбец координат вектора 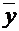(в том же базисе), т.е. Y = AX. Другими словами, каждому линейному оператору можно поставить в соответствие единственную квадратную матрицу этого оператора.

При переходе к другому базису в пространстве Rⁿ матрица линейного оператора изменится. Можно показать, что матрицы А^* и А линейного оператора 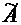в новом базисе 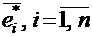и в старом базисе 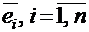, соответственно, связаны соотношением: 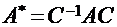, где С – матрица перехода от старого базиса к новому (см. подраздел 3.4).

Определение. Ненулевой вектор 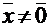называется собственным вектором линейного оператора 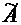(или линейного преобразования, заданного матрицей А), если существует такое число λ, что справедливо равенство: 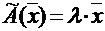. При этом число λ называется собственным значением оператора 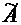(или матрицы А), соответствующим собственному вектору .

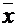Из приведенного определения следует, что собственный вектор под воздействием линейного оператора переходит в вектор, коллинеарный самому себе, т.е. просто умножается на число – собственное значение, ему соответствующее.

Характеристическим уравнением матрицы А линейного оператора называется уравнение:

.

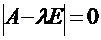где λ – неизвестное собственное значение, Е – единичная матрица.

ПРИМЕР: Для матрицы

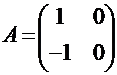
характеристическое уравнение будет иметь вид:

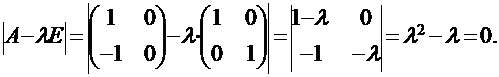
Таким образом, задача отыскания собственных векторов и собственных значений линейного оператора решается в следующей последовательности. Вна­чале составляют и решают характеристи­ческое уравнение. Его решениями будут собственные значения, причем их количество не превосходит n. После этого, подставляя последовательно каждое из найденных собственных значений в систему однородных уравнений вида:

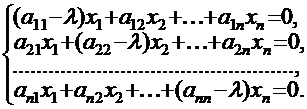
каждый раз решают ее методом Гаусса и выясняют структуру нетривиальных решений – координат собственного векто­ра, соответствующего данному собственному значению.

ПРИМЕР: Найдите собственные векторы линейного оператора, заданного матрицей:

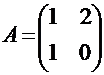
Составим характеристическое уравнение для отыскания собственных значений:

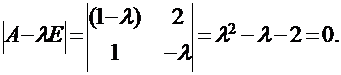
Решениями этого уравнения будут два собственных значения преобразования А: λ₁ = 2 и λ₂ = − 1.

Приступим к отысканию собственного вектора, соответствующего первому из собственных значений. Для этого запишем систему однородных уравнений:

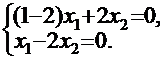
Полученная система фактически представляет собой одно уравнение с двумя неизвестными. Положим 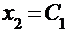и найдем 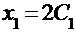. Таким образом, собственный вектор, соответствующий первому из собственных значений, будет иметь следующие координаты:

,

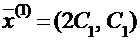где С₁ – любое действительное число, отличное от нуля.

Для второго собственного значения система однородных уравнений запишется в виде:

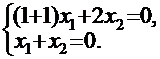
Т.е. представляет собой одно уравнение с двумя неизвестными. Полагая 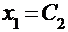, найдем 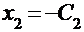, и окончательно запишем:

,

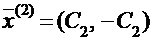где С₂ – любое действительное число, отличное от нуля.

Критерий Сильвестра

Для того чтобы квадратичная форма L = XTAX была положительно определенной, необходимо и достаточно, чтобы все главные миноры матрицы А этой формы были положительны.

В критерии Сильвестра под главными минорами матрицы понимают миноры i – го порядка, построенные следующим образом:

ПРИМЕР: Покажите положительную определенность квадратич­ной формы: .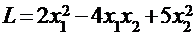

Найдем вначале матрицу этой формы. Поскольку эту форму можно переписать в виде: 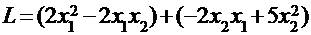, искомая матрица имеет вид:

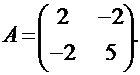
Характеристическое уравнение для этой матрицы будет иметь вид:

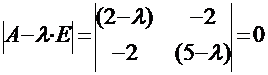, или: .

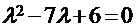Решая его, найдем: 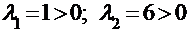, следовательно, на основа­нии первого критерия можно заключить, что данная квадратичная форма является положительно определенной.

Теперь найдем главные миноры матрицы А:

.

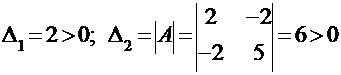Поскольку оба полученных минора положительны, на основании критерия Сильвестра заключаем, что данная квадратичная форма является положительно определенной.

Рекомендуемая литература по Теме 3:[1 ÷ 3].

ВОПРОСЫ для самопроверке знаний по теме 3:

1. При каком значении с векторы 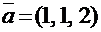и 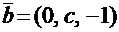будут перпендикулярны?

2. Сколько векторов будет содержать базис пространства ?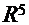

3. Можно ли образовать ортонормированный базис из двух векторов: ?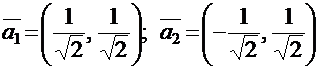

4. В какие векторы преобразует векторы (1, 0) и (0, 1) линейный оператор, заданный матрицей ?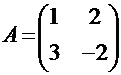

5. Является ли число 1 собственным значением матрицы ?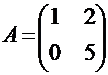

6. Будет ли положительно определенной квадратичная форма ?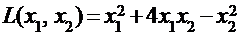

Уравнения плоскости

Пусть заданы: прямоугольная система координат Oxyz; произ­вольная плоскость p; точка 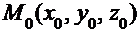, лежащая на плоскости p; а также вектор 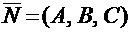, перпендикулярный плоскости p (рис. 4.1).

Рис. 4.1.

Рассмотрим на плоскости p произвольную точку 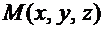. Очевидно, что эта точка будет лежать на плоскости p тогда и только тогда, когда векторы 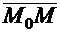и 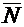будут взаимно перпендикулярны (ортогональны), т.е. когда их скалярное произведение будет равно нулю. Поскольку:

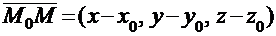и ,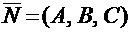

это условие можно записать в виде:

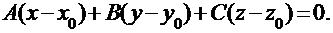Это уравнение и есть уравнение плоскости, проходящей через точку М₀ перпендикулярно вектору .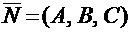

Если в последнем уравнении раскрыть скобки и ввести обозначение: 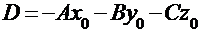, то получим общее уравнение плоскости:

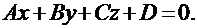При этом вектор 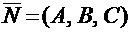, пер­пендикулярный плоскости p, называется нормальным вектором (или вектором нормали) этой плоскости.

Очевидно, что угол j между плоскостями, заданными общими уравнениям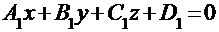и:

и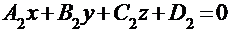

будет определяться углом j между нормальными векторам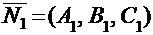и: и 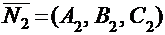этих плоскостей, а косинус этого угла может быть найден по формуле:

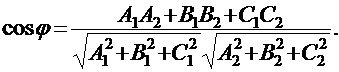Условие параллельности рассматриваемых плоскостей эквивалентно условию коллинеарности нормальных векторов этих плоскостей, т.е. может быть записано в виде:

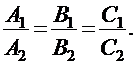В свою очередь, условие перпендикулярности плоскостей вытекает из условия перпендикулярности нормальных векторов, т.е. из равенства нулю их скалярного произведения, и может быть записано в виде:

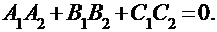ЛИТЕРАТУРА

1. Налимов В.Н. Основы линейной алгебры для экономистов и менеджеров: Учебное пособие. – М.: Издание ИМЭС, 2013.

2. Ильин В.А., Ким Г.Д. Линейная алгебра и аналитическая геометрия: Учебник. – М.: Проспект, 2012.

3. Малугин В.А. Математика для экономистов. Линейная алгебра: Курс лекций. – М.: Эксмо, 2006.

ТЕОРЕТИКО – ПРАКТИЧЕСКИЙ КУРС

«ОСНОВЫ ЛИНЕЙНОЙ АЛГЕБРЫ