Историческое развитие понятия «матрица»
Веретенников
Валентин Николаевич
ВЫСШАЯ МАТЕМАТИКА
ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
 |
Ρ Г Γ М У
Санкт-Петербург
МАТРИЦЫ
Историческое развитие понятия «матрица»
В 1850 г. английский математик Дж. Дж. Сильвестр (1814-1897) ввёл в математику понятиме «матрица» для обозначения прямоугольного упорядочения чисел.
С 1853 г. к изучению матриц приступил В.Р. Гамильтон (1805-1865), а с1858 г. ‒ А. Кэли (1821-1895).
Основополагающее значения понятия матрицы для математики было осознано лишь в конце XIX в.
Существенную роль в дальнейшем развитии ма ричного исчисления сыграл Г. Фробениус (1849-1917).
Созданное алгебраистами исчисление было в 1925 г. использовано В. Гейзенбергом (1901-1976) для описания квантовой механики.
В 1942 г. Фельдткайлер ввёл матричное исчисление в электротехнику для расчета электрических цепей.
Ряд примеров, взятых из разных областей человеческой деятельности, покажет целесообразность введения нового математического понятия «матрица».
Вводный прмер. Э.Ю. Берг, исследуя наиболее выдающиеся ливневые дожди разной продожительности на территории Европейской части за десятилетие (1903-1912), отметил занальную редукцию передельной интенсивности дождей.
Упорядоченная совокупность элементов
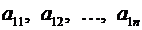– первая строкаматрицы,
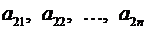– вторая строка и т.д.,
Упорядоченная совокупность элементов
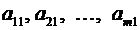– первый столбец,
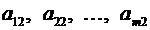– второй столбец и т.д.
В печатном тексте матрицы обозначаются прописными буквами латинского алфавита.
Для матрицы приняты также следующие обозначения:
.
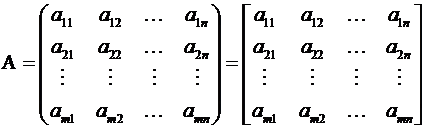Употребляются и более краткие обозначения
.
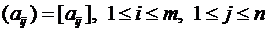В дальнейшем будем пользоваться обозначением матрицы с круглыми скобками.
Матрицу, имеющую 
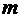строк и 
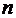столбцов, называют матрицей типа 
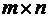(читается « 
»).
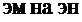В отдельных случаях употребляется также термин «размер матрицы».
То, что матрица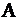 
имеет тип 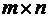, обозначается следующим
образом: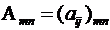 
.
Две матрицы, имеющие одинаковое количество строк и столбцов, называются матрицами одинакового типа.
Если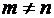 
, матрица называется прямоугольной.
Квадратная матрица
Квадратной называется матрица, у которой число строк равно числу столбцов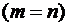 
, т.е. матрица вида
.
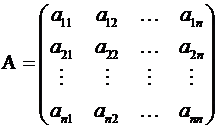В этом случае число 
называют порядком квадратной матрицы.
Квадратная матрица 1-го порядка отождествляется со своим единственным элементом, например (17).
При этом следует обратить внимание на то, что она является иным математическим объектом, чем вещественное число 17, и поэтому должна изображаться числом, заключенным в скобки.
Выпишем квадратные матрицыпервых трех порядков:
.
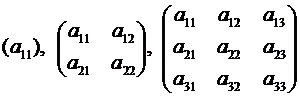Ø Элементы квадратной матрицы, имеющие одинаковые значения индексов
,
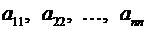составляют главную диагональ,
Ø а элементыквадратной матрицы порядка 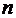, сумма индексов каждого из которых равна 
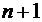, – побочную (или вторую) диагональ,
.
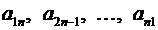Сумма элементов главной диагонали квадратной матрицы называется следомматрицы.
ОПРЕДЕЛИТЕЛИ
Найдём
.
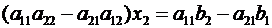Предполагая, что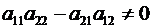 
, получаем
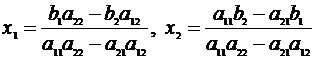. (2.2)
Непосредственной проверкой легко убедиться, что значения для неизвестных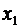 
и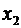 
, даваемые формулами (2.2), действительно удовлетворяют системе (2.1).
Таким образом, доказано, что если 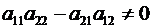, то система (2.1) имеет единственное решение, определяемое формулами (2.2).
Рассмотрим квадратную матрицу 2-го порядка, составленную из коэффициентов при неизвестных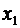 
и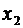 
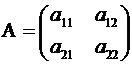, (2.3)
Определение. Определителем квадратной матрицы 2-го порядка (2.3) называется число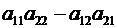 
, вычисляемое по следующему правилу:
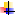надо взять произведение чисел, расположенных по главной диагонали (диагональ, идущая от левого верхнего угла к правому нижнему углу),
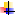и вычесть из него произведение чисел, расположенных на побочной диагонали (диагональ, идущая от правого верхнего элемента к левому нижнему).
Для определителя, как и для матрицы, используются такие понятия, как элемент, строка, столбец, главная и побочная диагональ и т.п.
Определитель квадратной матрицы 2-го порядка кратко называют определителем или детерминантом 2-го порядка.
Определитель квадратной матрицы (2.3) обозначается двумя вертикальными черточками:
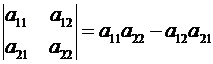. (2.4)
Кроме того, для определителя матрицы (1.3) применяются
обозначения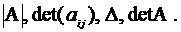 
(От французского слова determinant.)
Правило, по которому вычисляется определительматрицы 2-го порядка, схематически можно изобразить следующим образом:
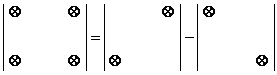или
– +
Пример. Вычислить определитель матрицы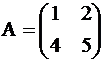 
.
▲ 
. ▼
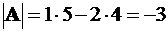Приняв введённое определение определителя 2-го порядка, замечаем, что числители в формулах (2.2) могут быть представлены
теперь в виде
,
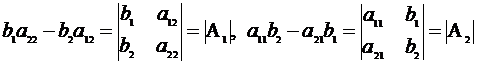где матрицы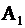 
и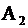 
получаются из матрицы 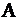заменой первого, соответственно второго, столбца на свободные члены.
Формулы (2.2) принимают теперь следующий вид:
.
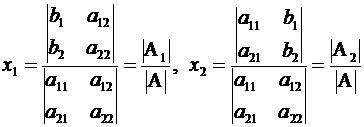Напомним еще раз, что эти формулы применимы лишь в случае, когда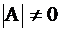 
.
Рассмотрим теперь систему трех линейных уравнений с тремя неизвестными
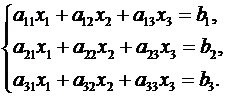(2.5)
Чтобы найтинеизвестное 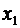, умножим уравнения системы (2.5) соответственно на выражения
,
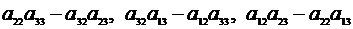и сложим, полученные левые и правые части.
После приведения подобных членов (относительно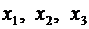 
) окажется, что коэффициенты при неизвестных 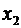и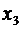 
равны нулю.
Предполагая, что коэффициентпри неизвестном 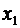отличенот нуля, получим
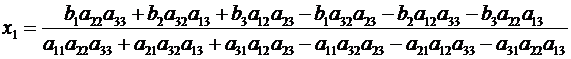. (2.6)
Рассмотрим квадратную матрицу 3-го порядка
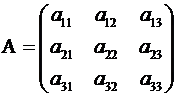. (2.7)
Матрица 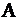составлена из коэффици..ентов при неизвестных 
.
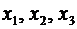Определение. Определителем квадратной матрицы 3-го порядка (2.7) называется число
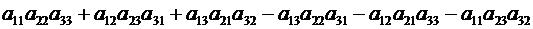
Определитель матрицы (2.7) кратко называют определителем 3-го порядка и обозначают двумя вертикальными чертами или одним из символов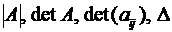 
.
Итак, по определению
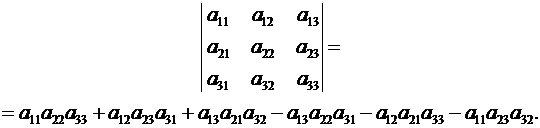(2.8)
Таким образом,
каждый членопределителя 3-го порядка представляет собой произведение трёх его элементов, взятых по одному из каждой строки и каждого столбца.
Эти произведения берутся с определенными знаками.
Со знаком плюс – три члена, состоящие из элементов главной диагонали и из элементов, расположенных в вершинах равнобедренных треугольников с основаниями, параллельными главной диагонали, и с вершиной в противоположном углу.
Со знаком минус – три члена, расположенные аналогичным образом относительно побочной диагонали.
Схематически это правило (правилоСаррюса или правилотреугольников) может быть изображено следующим образом:
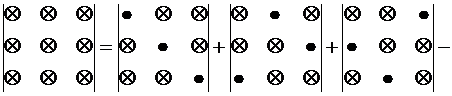
или
+ –
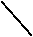
Пьер Фредерик Саррюс – французский математик.
Саррюс поступил на факультет естественных наук, окончив его со специализацией в математике в 1821 году.
С 1826 г. он преподавал в Страсбургском университете, с 1829 г. был профессором, в 1839‒1852 гг. деканом.
В 1858 г. по болезни вышел в отставку.
Пример. Вычислить определитель матрицы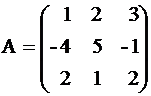 
.
▲ 
. ▼
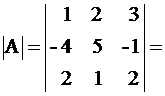
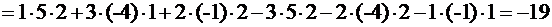Итак, знаменатель в формуле (2.6) представляется в виде определителя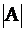 
.
Что касается числителя, то, поскольку он получается из знаменателя заменой чисел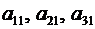 
соответственно на числа 
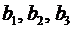– его можно представить в виде определителя
.
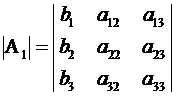Аналогичным образом, если уравнения системы (2.5) умножим последовательно на выражение
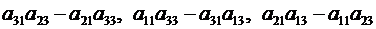
и результаты сложим, найдём формулу для неизвестного .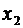
Наконец, умножая уравнения (2.5) последовательно на выражения
,
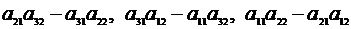найдем формулу для неизвестного .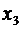
Окончательно будем иметь
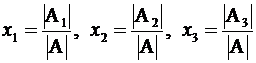, (2.9)
где матрицы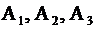 
получаются из матрицы 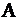заменой соответствующего столбца на свободные члены.
Если квадратная матрица 3-го порядка является треугольной, т.е. имеет вид
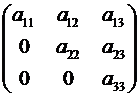или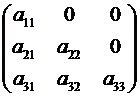 
,
то её определитель равен произведению элементов главной диагонали, т.е.
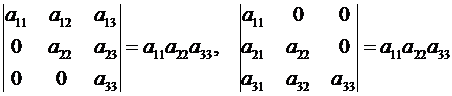. (2.10)
Равенства (2.10) следуют из формулы (2.8).
Свойства определителей
Вычислениеопределителей значительно облегчается, если пользоваться их свойствами.
Будем излагать свойстваопределителейна примереопределителей третьего порядка.
Свойство 3
Определитель с двумя одинаковыми строками (столбцами) равен нулю.
▲ Определитель (2.8) обозначим через символ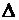 
.
Пусть он содержит два одинаковых столбца.
.
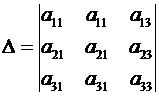Переставивэти столбцы, получим тот же определитель .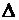
С другой стороны, по свойству 2 определитель изменит знак, т.е.
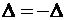, откуда 
. ▼
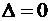Свойство 4
Если все элементы некоторой строки (столбца) определителя состоят из нулей, то определитель равен нулю.
▲ В самом деле, в каждое произведение алгебраической суммы в правой части (2.8) входит один элемент строки (столбца), состоящей из нулей.
Поэтому все слагаемые, из которых состоит определитель, будут равны нулю. ▼
Свойство 6
Определитель, содержащий две пропорциональные строки (столбца) равен нулю.
▲ Действительно, выделяя общий множительэлементов (коэффициент пропорциональности) одной из этих строк (столбцов) и вынося его за знакопределителя, получаем определительс двумя одинаковыми столбцами, равныйнулю. ▼
Свойство 7
Если все элементы 
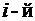строки ( 
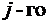столбца) определителя представлены в виде суммы двух слагаемых, то определитель равен сумме двух определителей,у которых все строки (столбцы),
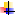кроме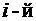 
строки ( 
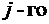столбца), те же, что и у данного определителя,
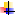
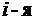строка ( 
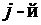столбец) одного определителя состоит из первых слагаемых элементов 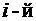строки ( 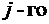столбца) данного определителя,
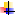а 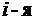строка ( 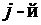столбец) другого определителя – из вторых слагаемых элементов 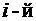строки ( 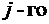столбца).
Доказать самостоятельно.
Свойство 8. (Прибавление кратной строки)
Определитель не изменится, если к элементам одной из его строк (столбцов) прибавить соответствующие элементы другой строки (столбца), умноженные на один и тот же множитель.
▲ Пусть, например, к элементам 3-го столбцаопределителя (2.8) прибавлены соответствующие элементы 2-го столбца, умноженные на множитель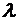 
.
Тогда
,
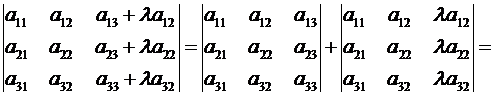
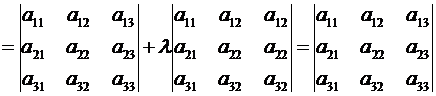поскольку
. ▼
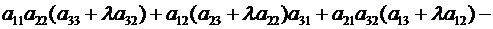
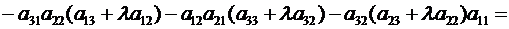
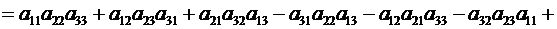
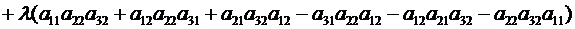Замечание.
(Добавление строки к строке,умноженной на число.)
Как было показано, добавление строки, умноженной на число, к другой строке не влияет на величину определителя.
Заметим, однако, что добавление строки к другой строке, умноженной на число, не является тем же самым и приводит к иным результатам.
Например, добавляяк первой строке, умноженной на число 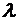, вторую строку, получим определитель
.
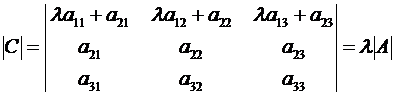Это происходит в связи с тем, что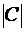 
получают 
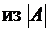путем умноженияпервой строки 
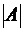на 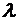и добавления к нейвторой строки.
Первый из этих двух шагов, как было показано, изменяет 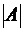на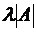 
, а второй не изменяет этой величины.
Отсюда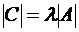 
.
Таким образом, в то время как строка, умноженная на число и добавленная к строке, не оказывает влияния наопределитель,
добавление строки к строке, умноженной на число, имеетсвоим последствием то, что определитель оказывается умноженным на этот множитель.
Эти же действия справедливы для столбца.
Применяя вышеуказанные свойстваопределителей, можно упростить задачу вычисленияопределителей.
Преобразования, не изменяющие величинуопределителя, называются элементарными.
Прибавим
Ø к элементам 1-й строки элементы 2-й строки, умноженные на (–2),
Ø и к элементам 3-й строки элементы 2-й, умноженные на (–3).
Тогда
. ▼
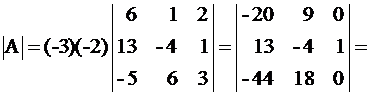
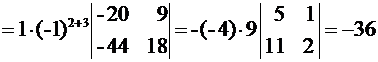Веретенников
Валентин Николаевич
ВЫСШАЯ МАТЕМАТИКА
ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
| |
Ρ Г Γ М У
Санкт-Петербург
МАТРИЦЫ
Историческое развитие понятия «матрица»
В 1850 г. английский математик Дж. Дж. Сильвестр (1814-1897) ввёл в математику понятиме «матрица» для обозначения прямоугольного упорядочения чисел.
С 1853 г. к изучению матриц приступил В.Р. Гамильтон (1805-1865), а с1858 г. ‒ А. Кэли (1821-1895).
Основополагающее значения понятия матрицы для математики было осознано лишь в конце XIX в.
Существенную роль в дальнейшем развитии ма ричного исчисления сыграл Г. Фробениус (1849-1917).
Созданное алгебраистами исчисление было в 1925 г. использовано В. Гейзенбергом (1901-1976) для описания квантовой механики.
В 1942 г. Фельдткайлер ввёл матричное исчисление в электротехнику для расчета электрических цепей.
Ряд примеров, взятых из разных областей человеческой деятельности, покажет целесообразность введения нового математического понятия «матрица».
Вводный прмер. Э.Ю. Берг, исследуя наиболее выдающиеся ливневые дожди разной продожительности на территории Европейской части за десятилетие (1903-1912), отметил занальную редукцию передельной интенсивности дождей.