Выборочный коэффициент корреляции

Измерение тесноты и направления связи является важной задачей изучения и количественного измерения взаимосвязи явлений.

Если известно (или предполагается), что между результативным и факторным признаками существует линейная связь, то для оценки ее тесноты используется выборочный коэффициент корреляции 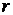(или просто коэффициент корреляции). Он чаще всего рассчитывается по формуле:

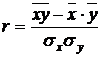. (25)

Коэффициент корреляции изменяется в пределах от –1 до +1. Равенство коэффициента нулю свидетельствует об отсутствиилинейной связи. Равенство коэффициента 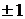показывает наличие функциональной связи. Знак «+» указывает напрямую связь (увеличение или уменьшение одного признака сопровождается аналогичным изменением другого признака), знак «–» – на обратную связь (увеличение или уменьшение одного признака сопровождается противоположным по направлению изменением другого признака).

В зависимости от того, насколько 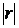приближается к 1, различают линейную связь слабую – 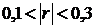, умеренную – 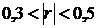, заметную – 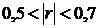, достаточно тесную – 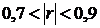и весьма тесную – .

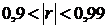В отличие от коэффициента регрессии 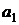коэффициент корреляции 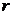не зависит от принятых единиц измерения признаков, а, следовательно, он сравним для любых признаков.

Как любая статистическая величина, коэффициент корреляции подвержен случайным колебаниям в результате выборочности исследования.

Для оценки значимости коэффициента корреляции применяется 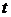-критерий Стьюдента. При этом определяется эмпирическое значение критерия :

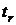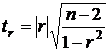. (26)

Вычисленное по формуле (27) значение 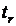сравнивается с критическим, которое берется из таблицы значений 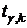распределения Стьюдента с учетом заданного уровня значимости 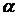( 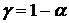) и числа степеней свободы .

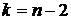Если 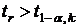, то величина коэффициента корреляции признается значимой.

Случайные процессы

Случайным процессом 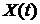называется процесс, значение которого при любом значении аргумента 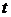является случайной величиной. Обычно 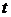– это время.

Пусть с течением времени в случайные моменты 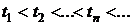происходит некоторое событие 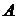. Обозначим 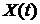число событий, имевших место в интервале 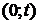. Для определенности начинаем отсчет времени в момент 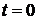, в который событие 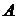не произошло, т.е. .

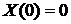Важнейшая математическая характеристика такого процесса – это вероятность того, что за время 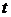событие 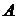произойдет ровно 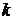раз:

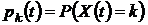, где ,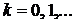

т.е. закон распределения целочисленной случайной величины .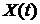

Процесс 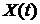называется процессом Пуассона (или простейшим потоком событий), если для него выполняются следующие предположения.

1. Процесс 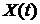является стационарным, т.е. вероятность появления числа событий 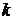во временном промежутке 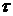, зависит только от длины этого промежутка (не зависит от начала отсчета).

2. Процесс 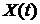– это процесс без последствий, т.е. вероятность появления 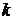событий на любом участке времени длины 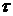не зависит от того, сколько событий появилось на любом другом не пересекающемся с ним участком.

3. Процесс 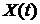– это ординарный процесс, т.е. вероятность того, что за малый промежуток времени 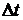событие 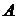произойдет более одного раза, есть величина более высокого порядка малости по сравнению с .

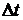Для пуассоновского процесса 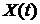функция 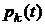имеет вид:

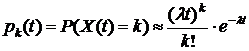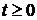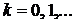, , (27)

Числовой параметр 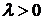называется интенсивностью пуассоновского потока, т.е. 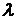– это среднее число событий 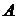, происходящих в единицу времени.

РЕШЕНИЕ ПРИМЕРНОГО ВАРИАНТА КОНТРОЛЬНОЙ РАБОТЫ

Задача 1. По каналу связи передаются три сообщения. Вероятность того, что первое сообщение будет искажено равна 0,1, второе – 0,2, третье – 0,3. Найти вероятности следующих событий: 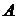– все три сообщения переданы без искажения; 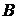– ровно одно сообщение передано без искажения; 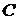– хотя бы одно сообщение искажено.

Решение.

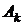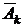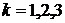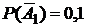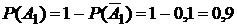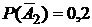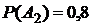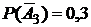Введем в рассмотрение вспомогательные события – k-ое сообщение передано без искажений, – k-ое сообщение искажено, . Согласно условию , тогда . Аналогично, и , и .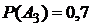

Так как событие 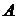можно представить в виде 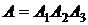и события 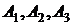независимы, то вероятность события 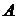можно найти по теореме умножения вероятностей для независимых событий:

.

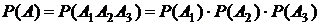
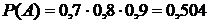Событие 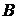можно представить следующим образом:

,

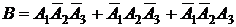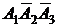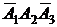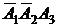причем слагаемые , и являются попарно несовместными событиями. Поэтому на основании теоремы сложения вероятностей (1) получаем:

.

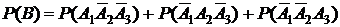Для вычисления вероятностей событи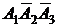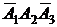й , и 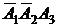используем теорему умножения вероятностей:

;

;

.

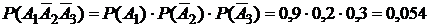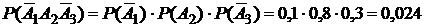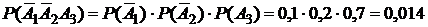Таким образом, окончательно получаем:

.

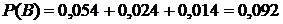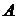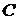События и являются противоположными, следовательно,

.

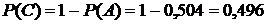Ответы: , , .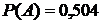

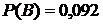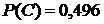Задача 2. Стрелок ведет стрельбу по цели с вероятностью попадания при каждом выстреле 0,4. За каждое попадание он получает 5 очков, а в случае промаха очков ему не начисляют. Составить закон распределения случайной величины 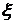– числа очков, полученных стрелком за 3 выстрела, построить многоугольник распределения, вычислить математическое ожидание, дисперсию и среднее квадратическое отклонение этой случайной величины.

Решение.

Случайная величина 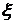может принимать 4 значения:

0 – если стрелок промахнулся 3 раза;

5 – если стрелок попал 1 раз при трех выстрелах;

10 – если стрелок попал 2 раза при трех выстрелах;

15 – если стрелок попал 3 раза.

Так как каждый выстрел можно рассматривать, как независимое испытание, в результате которого возможны только два исхода: попадание («успех») или промах («неудача»), то вероятности, соответствующие каждому значению случайной величины, можно найти по формуле Бернулли (5):

.

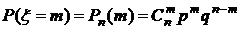По условию задачи имеем: число испытаний 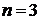, вероятность успеха 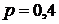, , 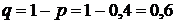значения 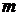будут изменяться от 0 до 3. Т.о. имеем:

,

,

,

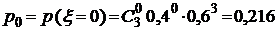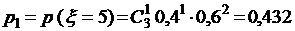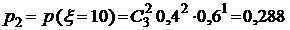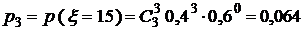.о

Следовательно, окончательно закон распределения случайной величины 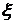будет иметь вид:

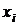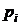	0,216	0,432	0,288	0,064

Построим многоугольник распределения. Для этого по оси абсцисс отложим возможные значения случайной величины, а по оси ординат – соответствующие им вероятности и соединяем точки (x_i, p_i) отрезками прямых. Полученная при этом ломаная линия и есть многоугольникраспределения вероятностей случайной величины .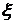

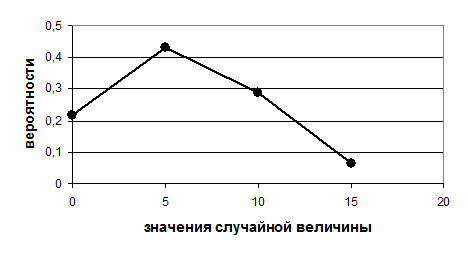Рис. 1. Многоугольник распределения вероятностей

Рассчитаем числовые характеристики случайной величины .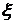

1. Математическое ожидание вычисляем по формуле (7)

.

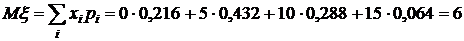2. Дисперсия вычисляется по формуле (9):

.

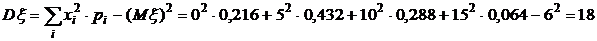3. Среднее квадратическое отклонение

.

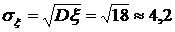Ответ. Закон распределения случайной величины :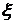

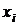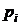	0,216	0,432	0,288	0,064

многоугольник распределения – на рисунке 1, , , .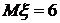

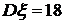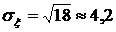Задача 3. Случайная величина 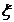распределена по нормальному закону с математическим ожиданием 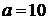и дисперсией 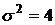. Найти вероятность того, что в результате испытания 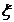примет значение, заключенное в интервале .

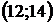Решение.

Так как случайная величина 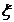имеет нормальное распределение, то вероятность ее попадания в интервал можно найти по формуле (11). Учитывая, что по условию имеем: 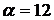, , 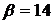, , 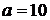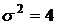то получим:

.

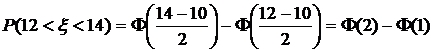По таблице значений функции Лапласа 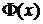находим: F(2)=0,4772, F(1)=0,3413. Значит, получаем: .

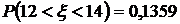Ответ: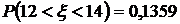

Задача 4. По выборке из генеральной совокупности нормально распределенного количественного признака X найти: 1) числовые характеристики выборки – выборочную среднюю, выборочную дисперсию, среднее квадратическое отклонение; 2) несмещенные оценки для генеральной средней и генеральной дисперсии; 3) доверительный интервал для оценки генеральной средней с надежностью .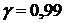

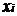	33,2	38,2	43,2	48,2	53,2

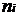Решение.

1. Сначала вычислим числовые характеристики выборки.

Выборочную среднюю найдем по формуле (14).

Учитывая, что объем выборки 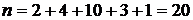, получаем:

.

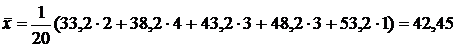Выборочную дисперсию удобнее вычислять по формуле (16):

.

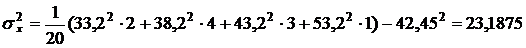Выборочное СКО:

.

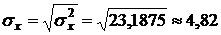2. Несмещенной оценкой для генеральной средней 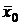является выборочная средняя .

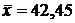Несмещенной оценкой дисперсии 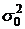генеральной совокупности является исправленная выборочная дисперсия 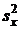, которая вычисляется по формуле (17):

.

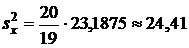3. Так как генеральная дисперсия 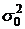неизвестна, а известна лишь ее оценка – исправленная выборочная дисперсия 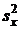и данная выборка имеет небольшой объем ( 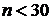), то доверительный интервал для генеральной средней можно найти, используя формулы (19) и (21).

Значение 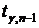находим по таблице распределения Стьюдента, где 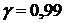– доверительная вероятность, 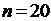– объем выборки, 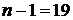- число степеней свободы.

Учитывая, что 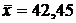, , 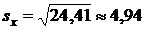, 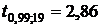находим сначала точность оценки по формуле (21):

.

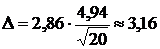Теперь искомый доверительный интервал определяем по формуле (19):

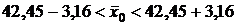
или .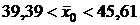

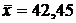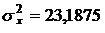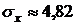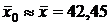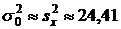Ответы: 1. , , ; 2. , ; 3. .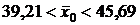

Задача 5. Массовую долю (%) оксида меди в минерале определили методом иодометрии и методом комплексометрии. По первому методу получили результаты: 38,20; 38,00; 37,66, а по второму: 37,70; 37,65; 37,55. Проверить, различаются ли средние результаты данных методов на уровне значимости 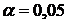, если известно, что результаты измерений имеют нормальный закон распределения с неизвестными, но равными дисперсиями.

Решение.

Вычисляем для каждого метода числовые характеристики, учитывая, что объем каждой выборки равен :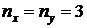

· выборочные средние значения по формуле (14):

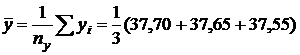=37,63;

· исправленные выборочные дисперсии по формуле (18):

,

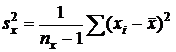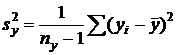
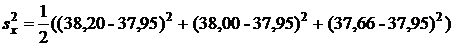=0,07453;

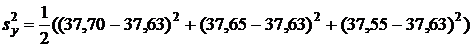=0,00583.

Теперь проверим гипотезу о равенстве средних двух совокупностей.

1. Нулевая гипотеза: : .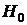

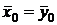Альтернативная гипотеза: :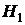

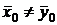
2. Уровень значимости .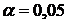

3. Проверку гипотезы будем проводить с помощью 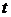-критерия, так как выборки маленькие и по условию дисперсии генеральных совокупностей неизвестны, но равны. По таблице значений 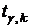распределения Стьюдента при 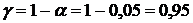и числе степеней свободы 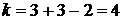находим критическое значение: .

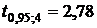4. Рассчитаем эмпирическое значение 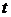-критерия, используя формулу (22):

.

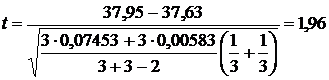Сравним полученное значение 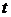с табличным значением 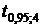. Так как 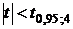, то гипотеза 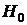принимается.

5. Гипотеза о равенстве средних значений двух методов проверена на уровне значимости 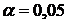с помощью 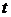-критерия и принята. Следовательно, результаты обоих методов отражают истинное содержание 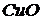в минерале.

Ответ: гипотеза 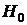о равенстве средних проверена на уровне значимости 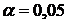с помощью 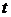-критерия и принята.

Задача 6. Имеются следующие данные об уровне механизации работ 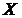(%) и производительности труда 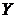(т/чел.) для 14 однотипных предприятий:

№ п/п

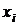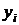№ п/п

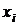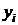Требуется: 1) оценить тесноту и направление связи между признаками с помощью коэффициента корреляции и оценить значимость коэффициента корреляции на уровне значимости 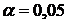; 2) найти уравнение линейной регрессии 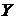на 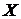; 3) в одной системе координат построить эмпирическую и теоретическую линии регрессии.

Решение.

1. Для удобства проведем все необходимые предварительные расчеты в таблице.

Таблица 1

Расчетная таблица

№ п/п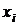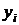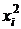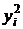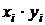
Всего

Рассчитаем числовые характеристики выборки, используя итоговую строку расчетной таблицы и учитывая, что объем выборки :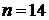

· выборочные средние:

;

;

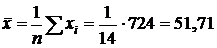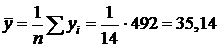· средние по квадратам:

;

;

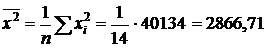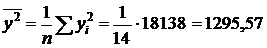· средняя по произведениям:

;

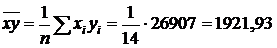· выборочные средние квадратические отклонения:

; ;

; .

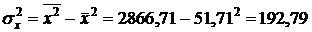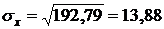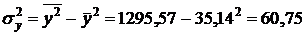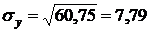Вычислим выборочный коэффициент корреляции по формуле (26):

.

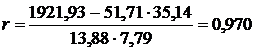Т.к. 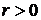и 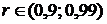, то, следовательно, линейная связь между изучаемыми признаками является прямой и весьма тесной.

Оценим значимость выборочного коэффициента корреляции. Для этого рассчитаем эмпирическое значение 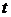-критерия по формуле (26):

.

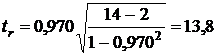Для уровня значимости 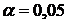и числа степеней свободы 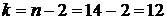находим критическое значение 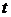-критерия: 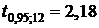по таблице значений 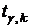распределения Стьюдента. Поскольку , то коэффициент корреляции между признакам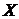и и 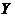является значимым (или значимо отличается от нуля).

2. Найдем уравнение линейной регрессии 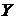на 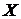: 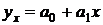, вычислив параметры уравнения регрессии по формулам (23) и (24):

;

.

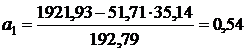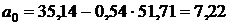Следовательно, уравнение прямой регрессии имеет вид:

.

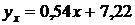3) Построим в одной системе координат эмпирическую и теоретическую линии регрессии. Эмпирическая линия – это ломаная, соединяющая точки с координатами 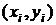, а теоретическая – это график прямой регрессии, уравнение которой было получено в п. 2. Теоретическую линию регрессии можно построить по двум точкам, абсциссы которых выбираются произвольно, а ординаты находятся по построенному уравнению регрессии. Найдем координаты точек для построения теоретической линии регрессии: 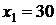, тогда 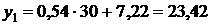; 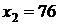, 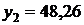. Значит, теоретическую линию регрессии будем строить по двум точкам с координатам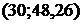и и .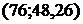

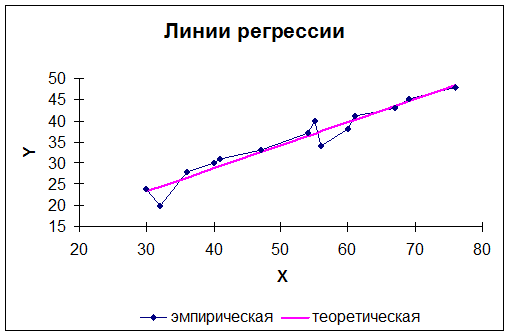Рис. 2. Эмпирическая и теоретическая линии регрессии

Ответ: 1) 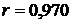, линейная связь прямая, весьма тесная, коэффициент корреляции значим на уровне значимости 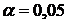; 2) выборочное уравнение прямой регрессии 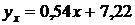; 3) линии регрессии представлены на рис. 2.

Задача 7. Среднее число заказов такси, поступающих на диспетчерский пункт в одну минуту, равно 3. Найти вероятность того, что за 2 минуты поступит: 1) четыре вызова; 2) менее четырех вызовов; 3) не менее четырех вызовов.

Решение.

Случайные события – заказы такси – представляют собой процесс Пуассона .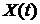

По условию имеем: интенсивность потока – среднее число заказов в единицу времени – 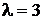, промежуток времени .

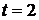1) Искомая вероятность того, что за 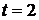минуты поступит ровно 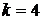вызова можно вычислить по формуле (28). Имеем:

.

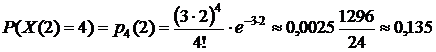2) Событие "поступило менее четырех вызовов" произойдет, если за время 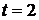мин. наступит одно из следующих несовместных событий: «поступило три вызова» – 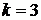, «поступило два вызова» – 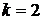, «поступил один вызов» – 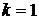, «не поступило ни одного вызова» – 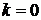. Таким образом, искомую вероятность находим с помощью теоремы сложения вероятностей (1):

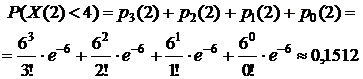
3) События "поступило не менее четырех вызовов" и "поступило менее четырех вызовов" противоположны, поэтому искомую вероятность того, что за две минуты поступит не менее 4 вызовов, можно найти по формуле (3):

.

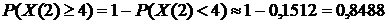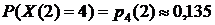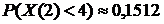Ответы: 1) ; 2) ; 3)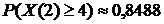

СПИСОК ЛИТЕРАТУРЫ

1. Кремер, Н. Ш. Теория вероятностей и математическая статистика : учеб. для вузов / Н. Ш. Кремер. – М. : ЮНИТИ-ДАНА, 2002. – 543 с.

2. Письменный, Д. Т. Конспект лекций по теории вероятностей и математической статистике / Д.Т. Письменный. – М. : Айрис-пресс, 2004. – 256 с. – (Высшее образование).

3. Гмурман, В. Е. Теория вероятностей и математическая статистика : учеб. пособие для вузов / В. Е. Гмурман. – М. : Высш. шк., 1997. – 479 с. : ил.

4. Гмурман, В. Е. Руководство к решению задач по теории вероятностей и математической статистике / В. Е. Гмурман. – М. : Высш. шк., 1998. – 400 с. : ил.

5. Данко, П. Е. Высшая математика в упражнениях и задачах. В 2 ч. Ч. 2 : учеб. пособие для вузов. / П. Е. Данко, А. Г. Попов, Т. Я. Кожевникова. – М. : Оникс : Мир и образование, 2005. – 416 с.

[1] Понятия “элементарное событие” и “происходит” являются первоначальными неопределяемыми понятиями, подобно геометрическим понятиям “точка” и “лежит”. При общих рассуждениях полезно иметь в виду какой-либо простой конкретный эксперимент типа общепонятного бросания монеты, игральной кости, извлечения карты из колоды и т.п.

[2] Построение интервальных вариационных рядов целесообразно не только при непрерывной вариации признака, но и если дискретная вариация проявляется в широких пределах, т.е. число вариантов дискретного признака достаточно велико.