Раздел 2. математический анализ
ТЕМА 4. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
Задание 1. Найти предел функции.
1. 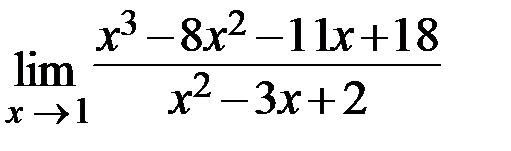 2.
2. 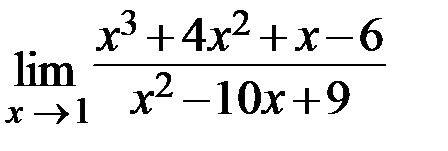
3. 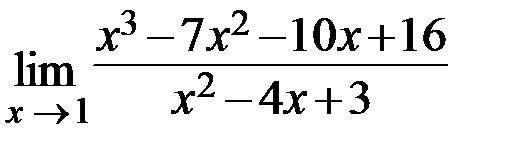 4.
4. 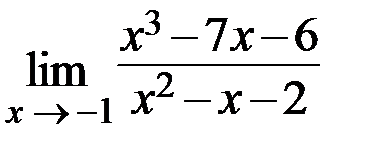
5. 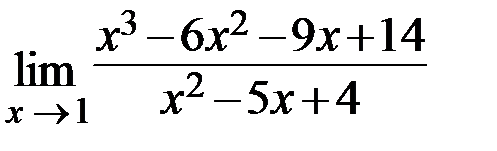 6.
6. 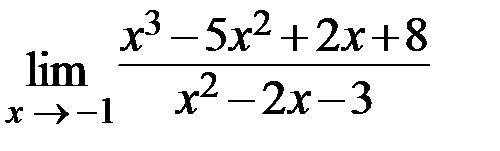
7. 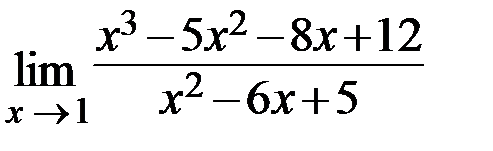 8.
8. 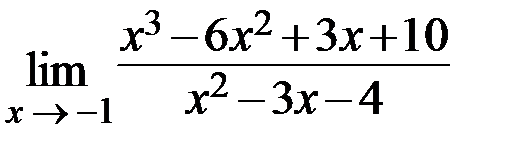
9. 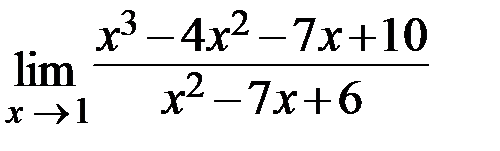 10.
10. 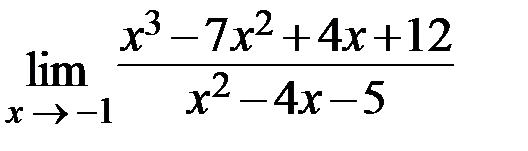
11. 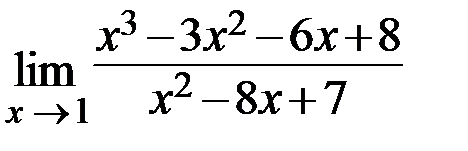 12.
12. 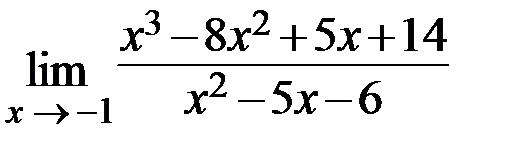
13. 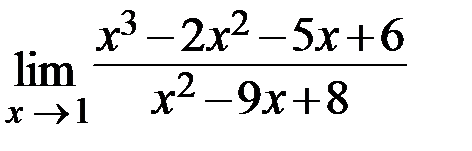 14.
14. 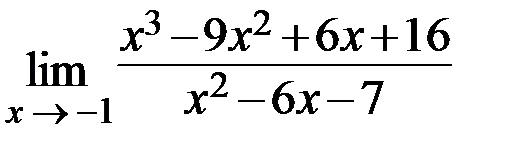
15. 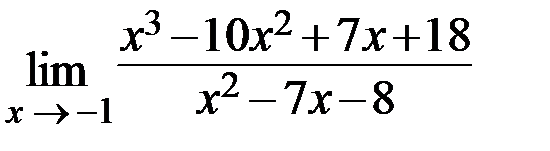 16.
16. 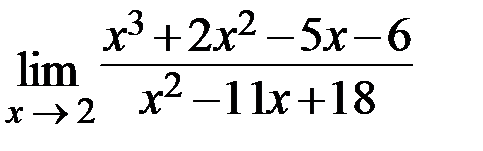
17. 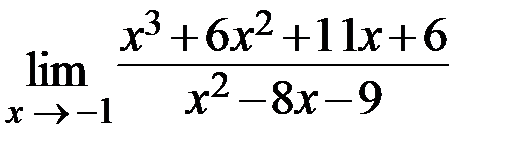 18.
18. 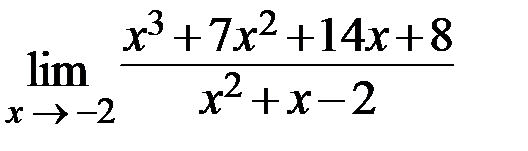
19. 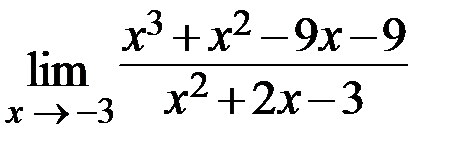 20.
20. 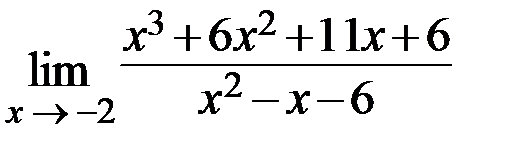
21. 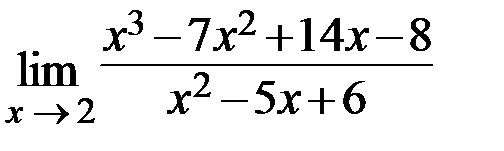 22.
22. 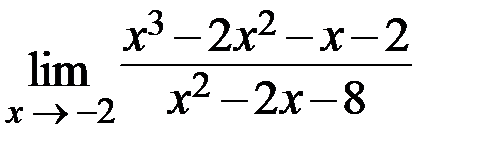
23. 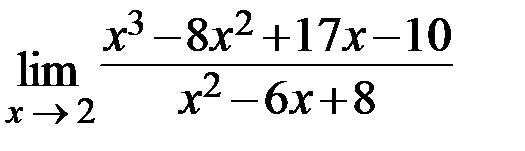 24.
24. 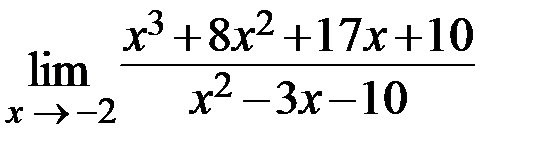
25. 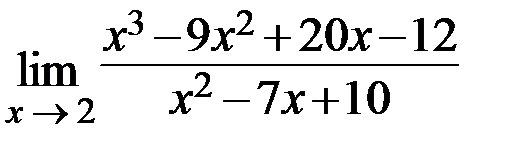 26.
26. 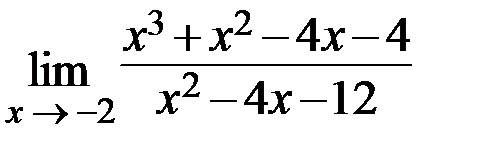
27. 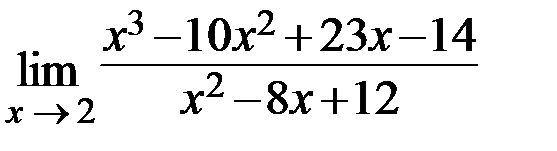 28.
28. 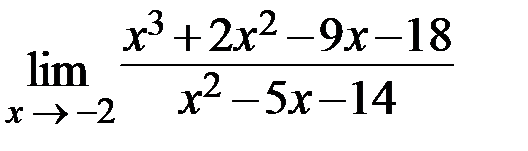
29. 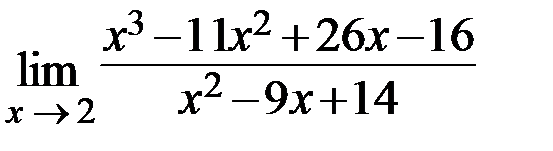 30.
30. 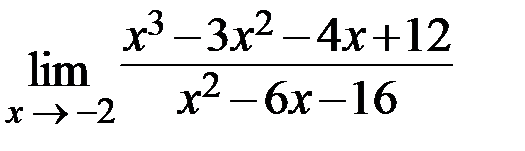
31. 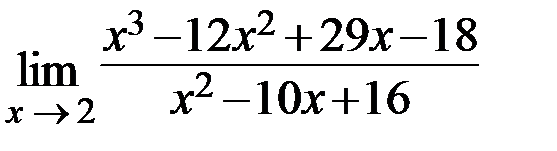 32.
32. 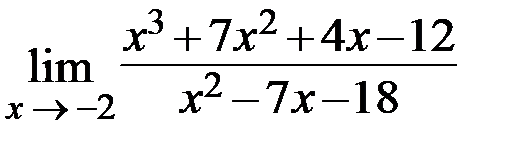
Пример. 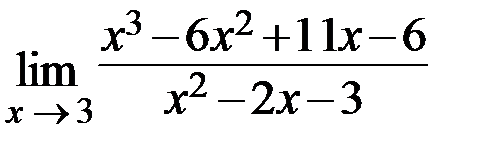 .
.
Решение. Здесь имеет место неопределённость вида 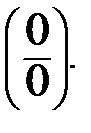 Разложим на множители числитель и знаменатель дроби. Для этого найдём корни числителя и знаменателя. Корни знаменателя можно подобрать по теореме Виетта. Один из корней известен: х=3, тогда другой корень будет х=−1 и
Разложим на множители числитель и знаменатель дроби. Для этого найдём корни числителя и знаменателя. Корни знаменателя можно подобрать по теореме Виетта. Один из корней известен: х=3, тогда другой корень будет х=−1 и 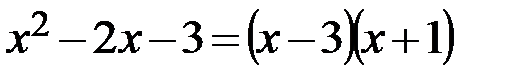 .
.
Один из корней числителя: х=3, тогда, разделив столбиком выражение числителя на х−3, получаем в частном 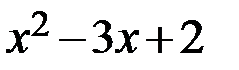 и записываем следующее разложение числителя на множители:
и записываем следующее разложение числителя на множители: 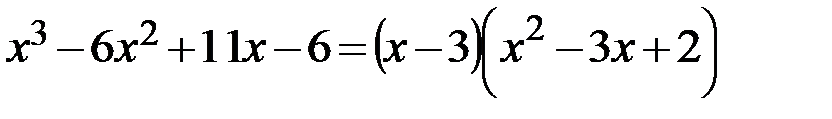 . Разложим на множители выражение
. Разложим на множители выражение 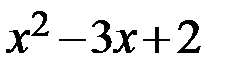 :
: 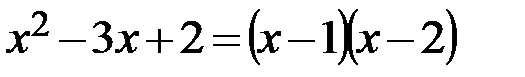 . Тогда:
. Тогда: 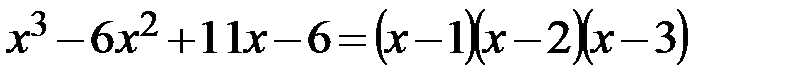 .
.
Возвращаемся к вычислению предела:
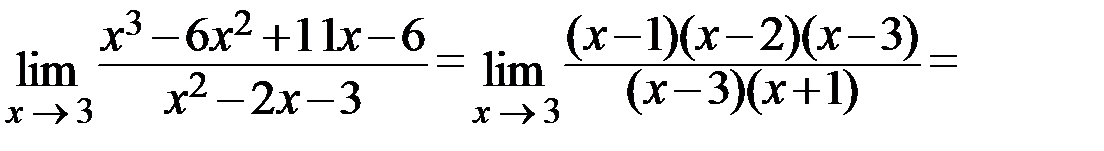
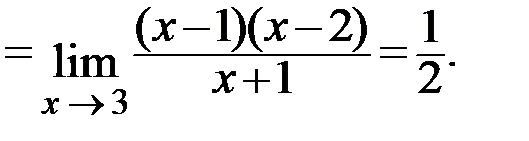
Ответ: 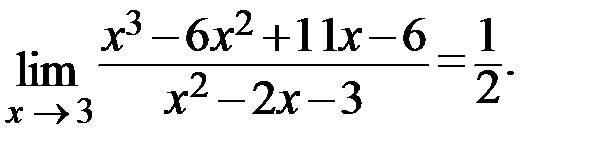
Задание 2. Найти предел функции.
1. 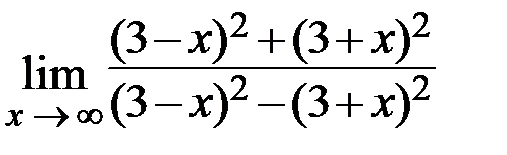 2.
2. 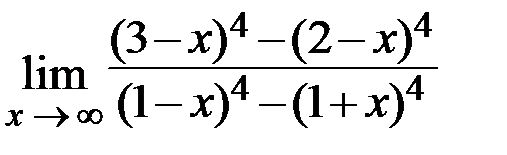
3. 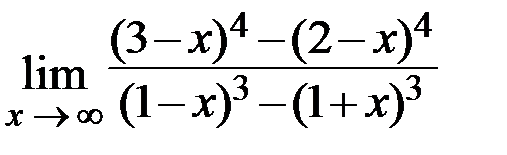 4.
4. 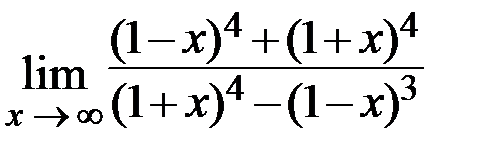
5. 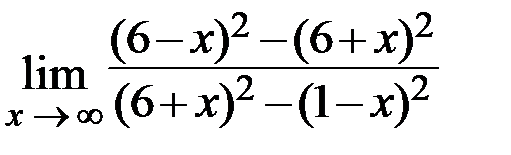 6.
6. 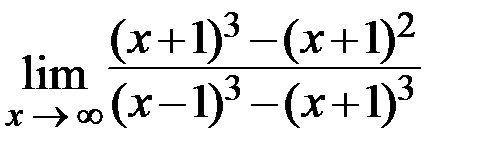
7. 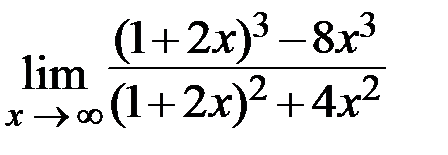 8.
8. 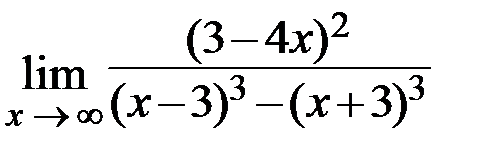
9. 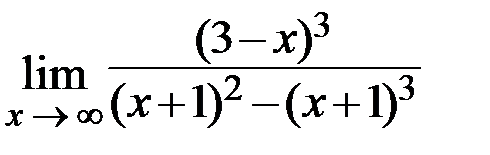 10.
10. 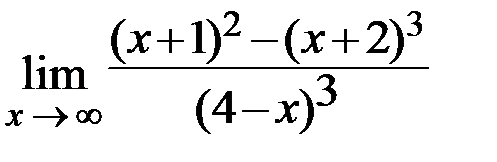
11. 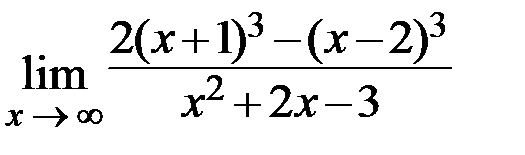 12.
12. 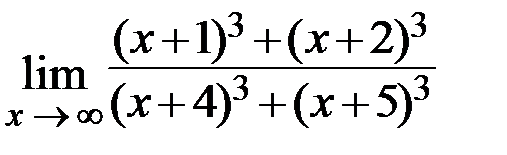
13. 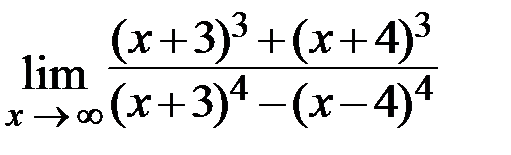 14.
14. 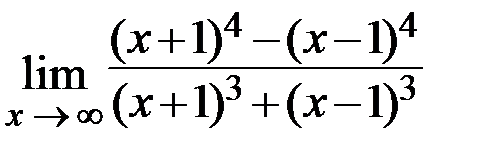
15. 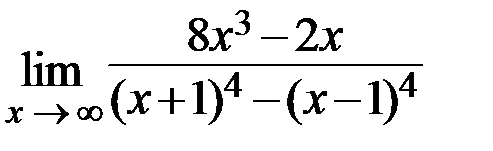 16.
16. 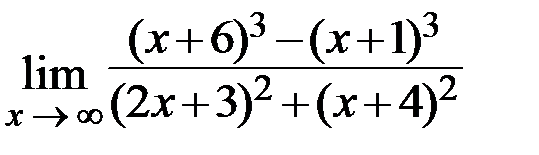
17. 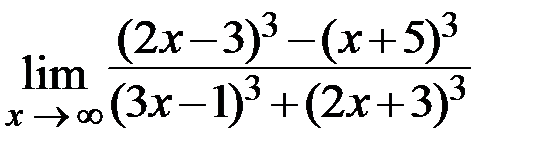 18.
18. 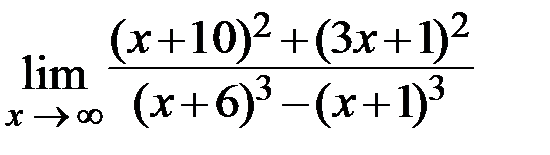
19. 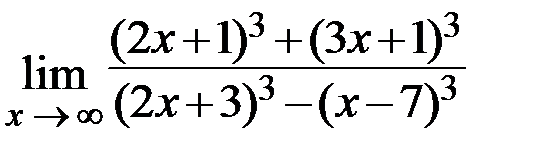 20.
20. 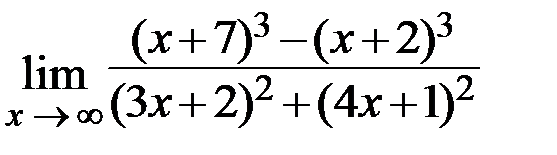
21. 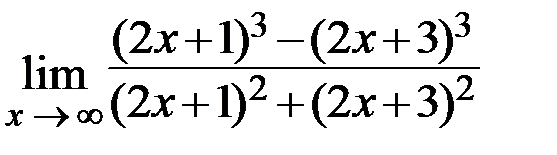 22.
22. 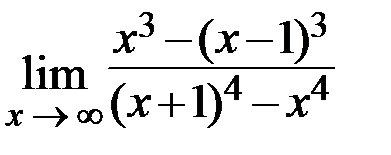
23. 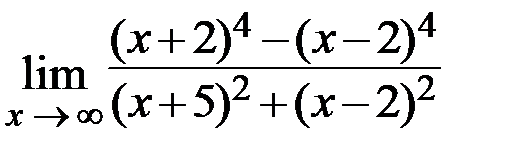 24.
24. 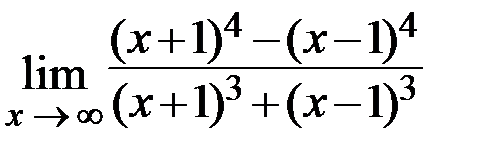
25. 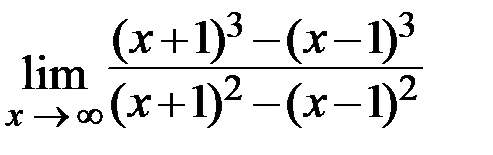 26.
26. 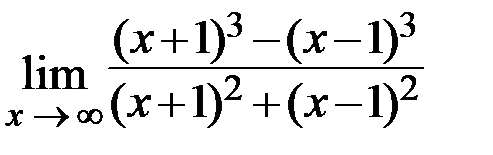
27. 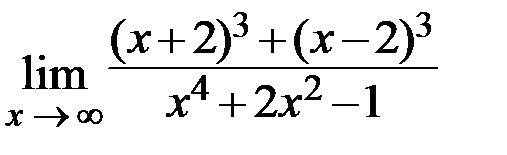 28.
28. 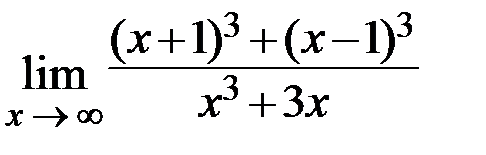
29. 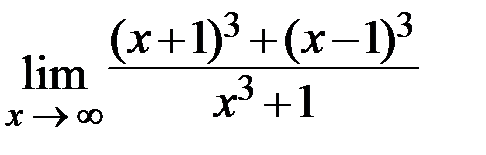 30.
30. 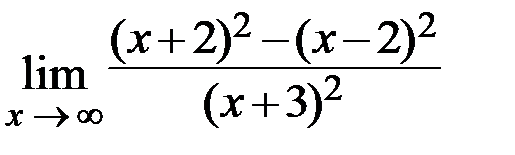
31. 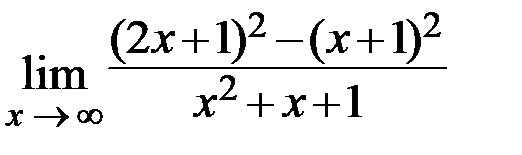 32.
32. 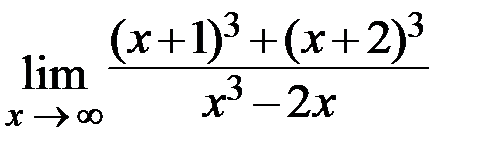
Пример. 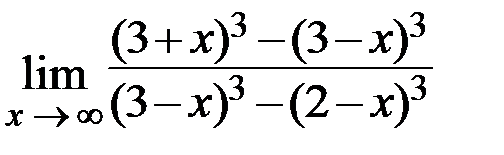 .
.
Решение. Здесь имеет место неопределённость вида 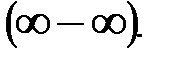 Преобразуем выражение, стоящее под знаком предела, воспользовавшись формулой разности кубов
Преобразуем выражение, стоящее под знаком предела, воспользовавшись формулой разности кубов 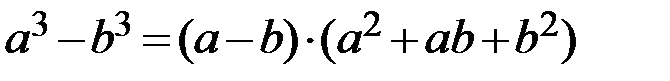 :
:
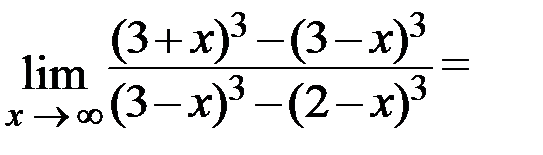
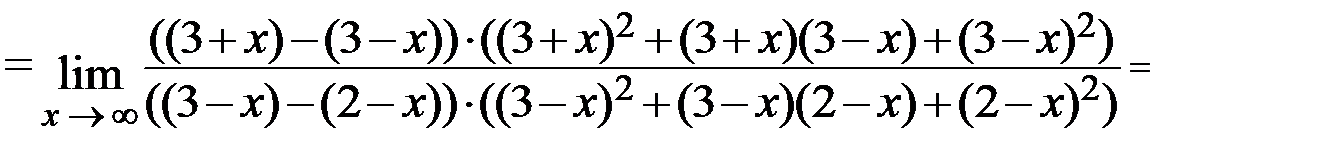
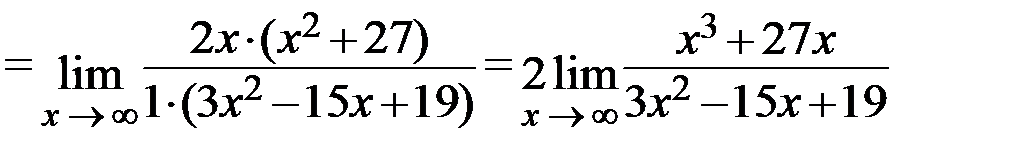 . Здесь возникает неопределённость вида
. Здесь возникает неопределённость вида 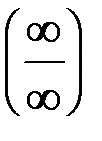 . Для её раскрытия разделим числитель и знаменатель на старшую степень
. Для её раскрытия разделим числитель и знаменатель на старшую степень 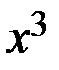 :
:
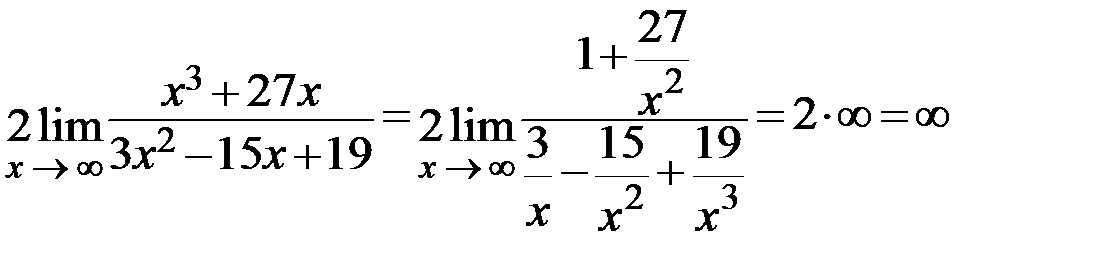 .
.
Ответ: 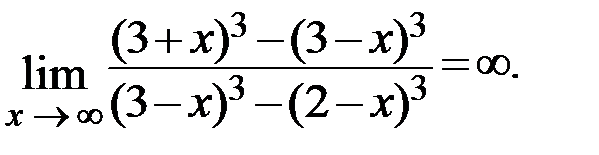
Задание 3. Найти производную 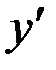 от заданной функции y.
от заданной функции y.
1. 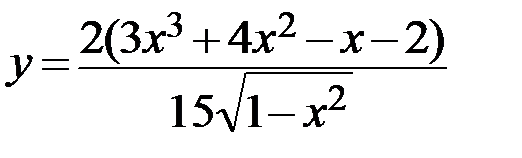 2.
2. 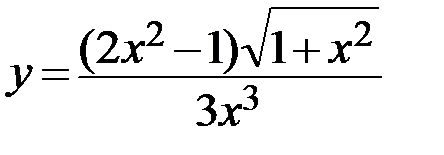
3. 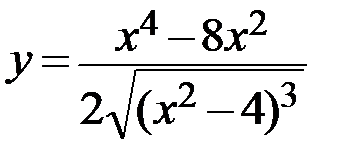 4.
4. 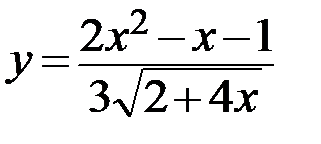
5. 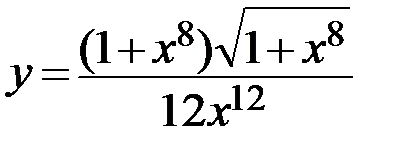 6.
6. 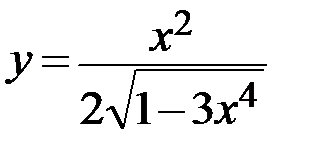
7. 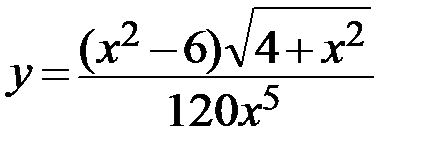 8.
8. 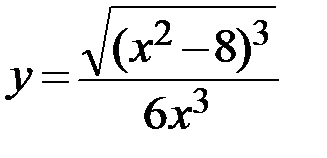
9. 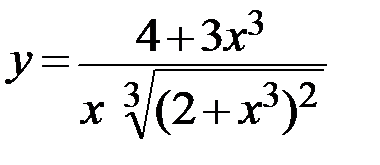 10.
10. 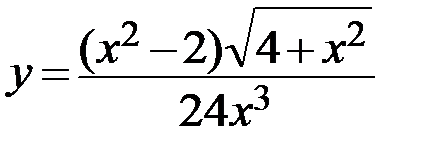
11 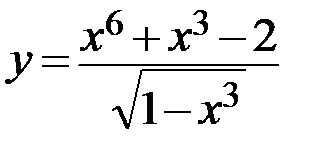 12.
12. 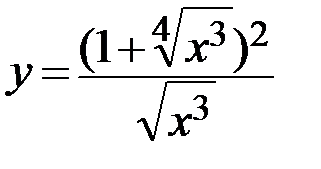
13. 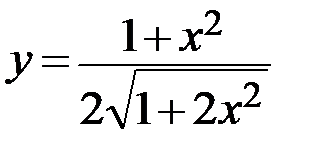 14.
14. 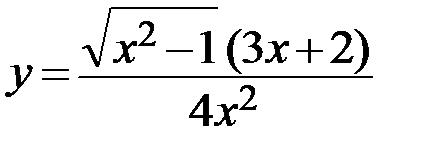
15. 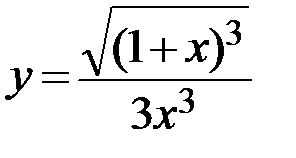 16.
16. 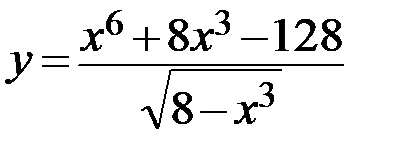
17. 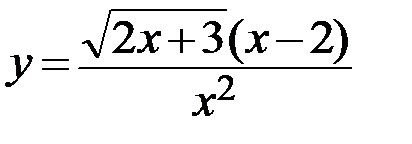 18.
18. 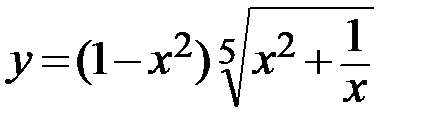
19. 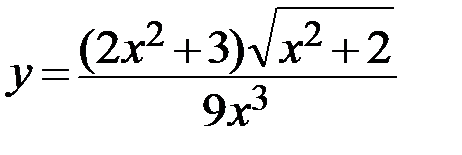 20.
20. 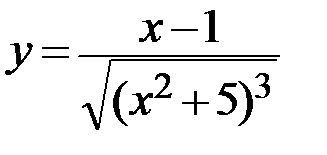
21. 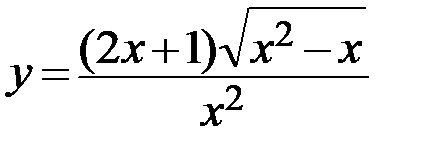 22.
22. 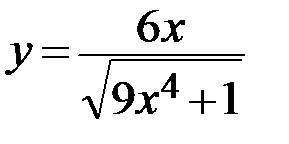
23. 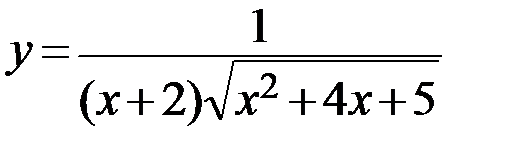 24.
24. 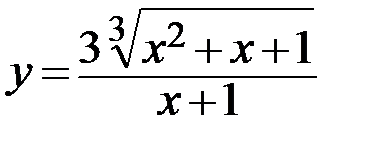
25. 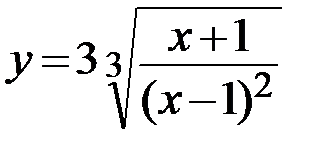 26.
26. 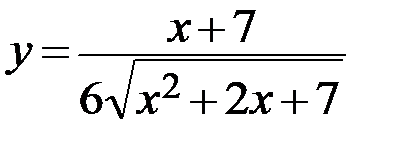
27. 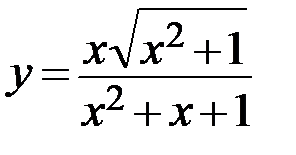 28.
28. 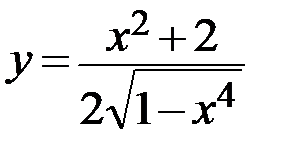
29. 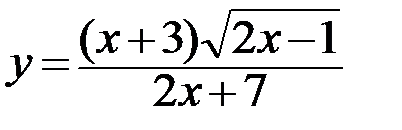 30.
30. 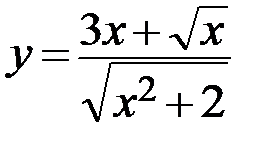
31. 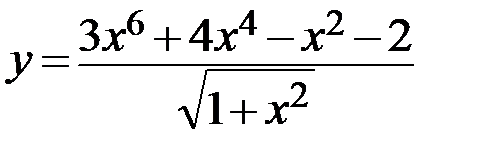 32.
32. 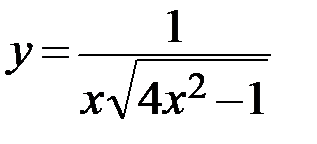
Пример. 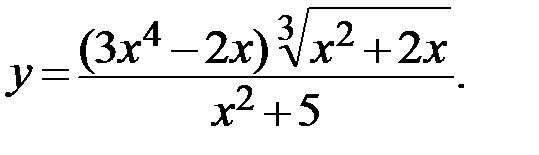
Решение. Воспользуемся правилами дифференцирования произведения ( 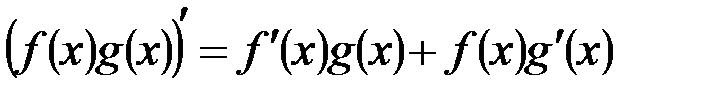 ), дроби (
), дроби ( 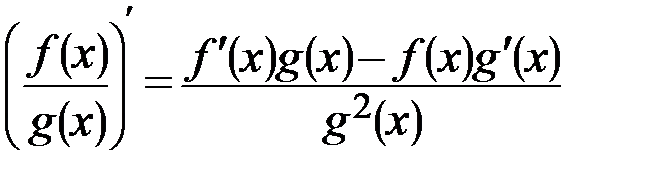 ) и сложной функции (
) и сложной функции ( 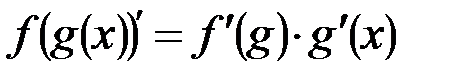 ):
):
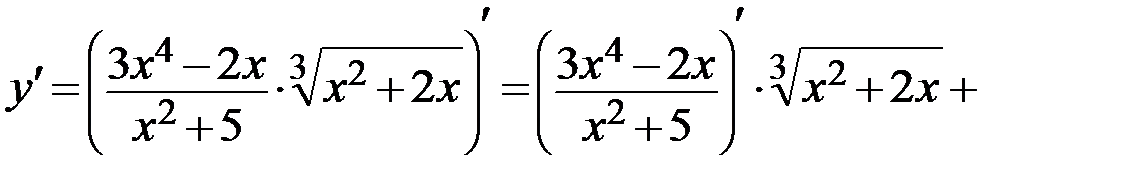
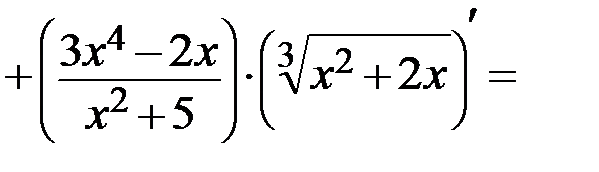

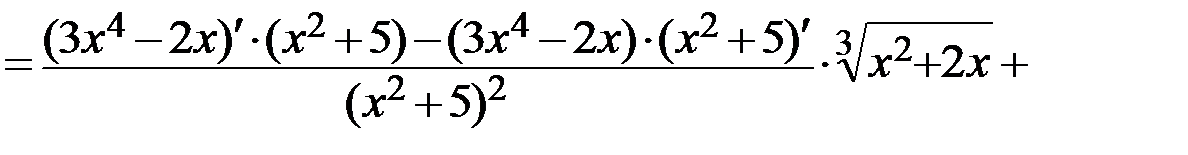
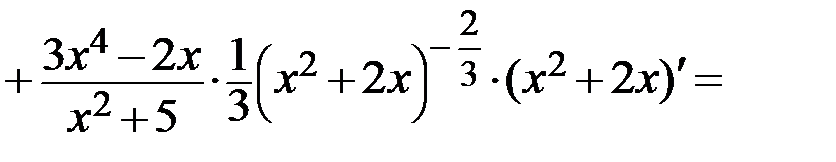
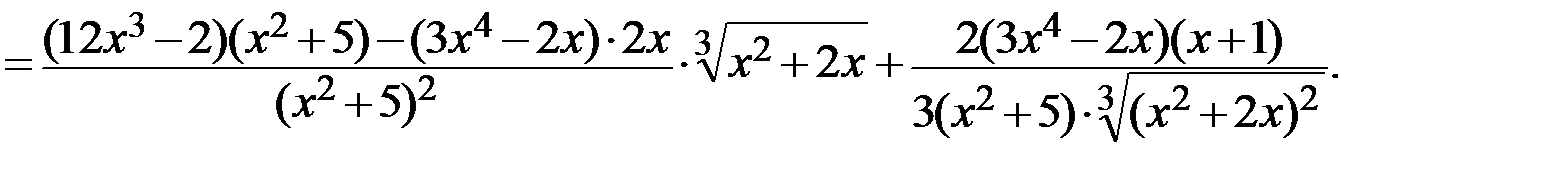
Задание 4. Найти производную 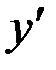 от заданной функции y.
от заданной функции y.
1. 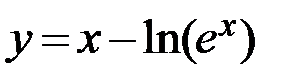 2.
2. 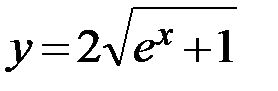
3. 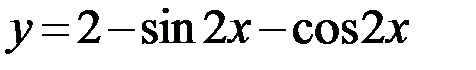 4.
4. 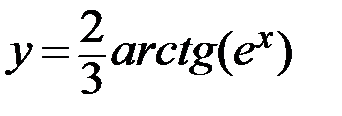
5. 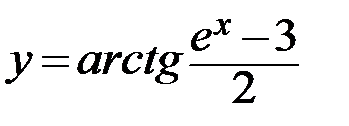 6.
6. 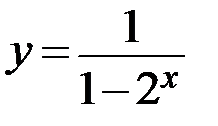
7. 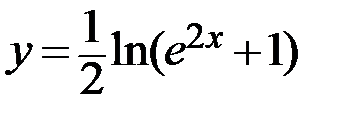 8.
8. 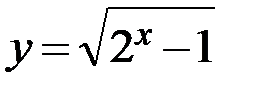
9. 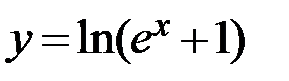 10.
10. 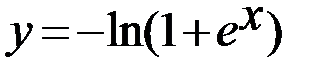
11. 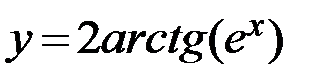 12.
12. 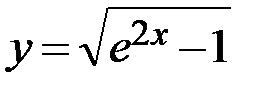
13. 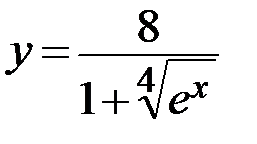 14.
14. 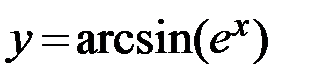
15. 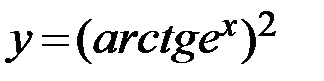 16.
16. 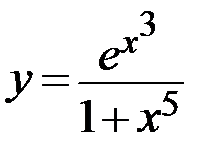
17. 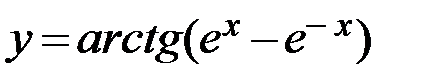 18.
18. 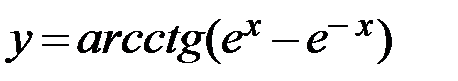
19. 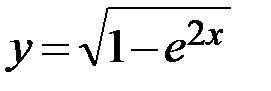 20.
20. 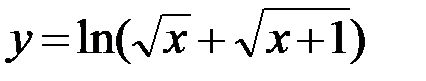
21. 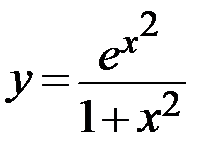 22.
22. 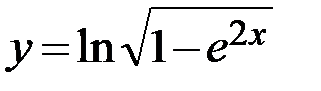
23. 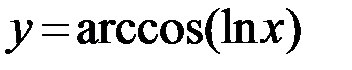 24.
24. 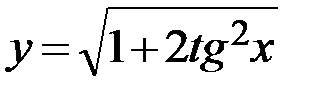
25. 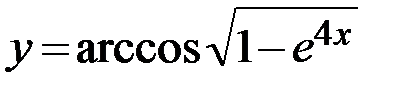 26.
26. 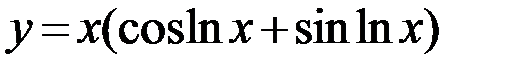
27. 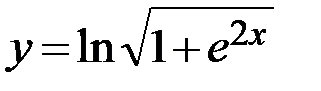 28.
28. 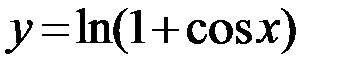
29. 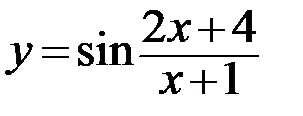 30.
30. 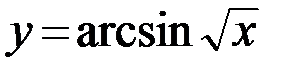
31. 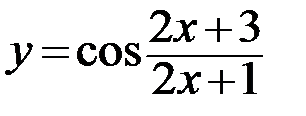 32.
32. 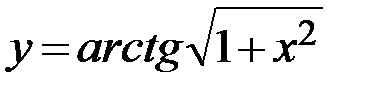
Пример. 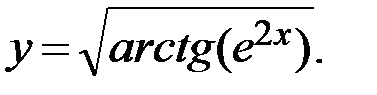
Решение. Воспользуемся правилом нахождения производной сложной функции:
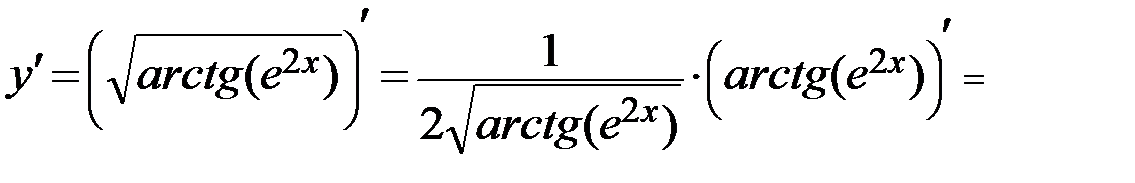
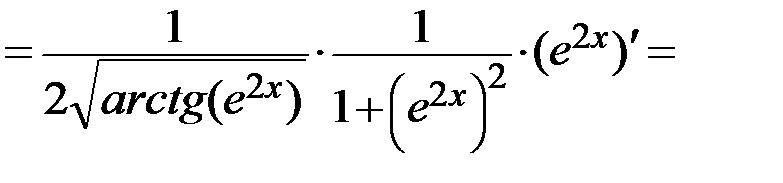
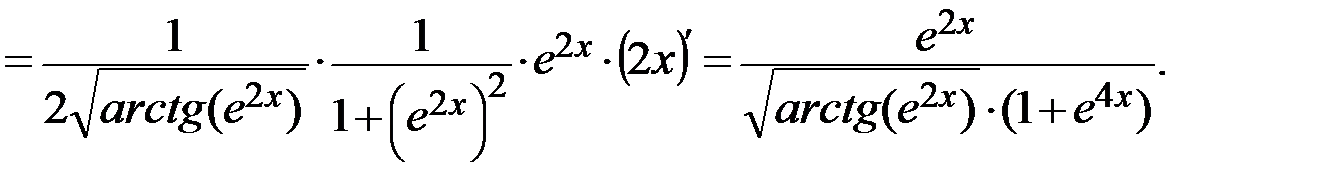
Задание 5. Вычислить предел функции, используя правило Лопиталя (функции взять из задания №1).
Пример. 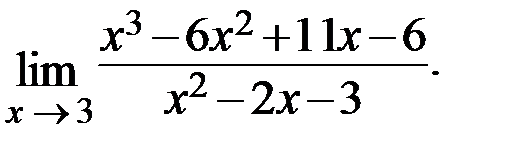
Решение. Здесь имеет место неопределённость вида 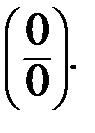 В этом случае по правилу Лопиталя, если существует предел отношения производных числителя и знаменателя, то существует и предел отношения исходных бесконечно малых функций, и эти пределы равны между собой. Тогда получаем:
В этом случае по правилу Лопиталя, если существует предел отношения производных числителя и знаменателя, то существует и предел отношения исходных бесконечно малых функций, и эти пределы равны между собой. Тогда получаем:
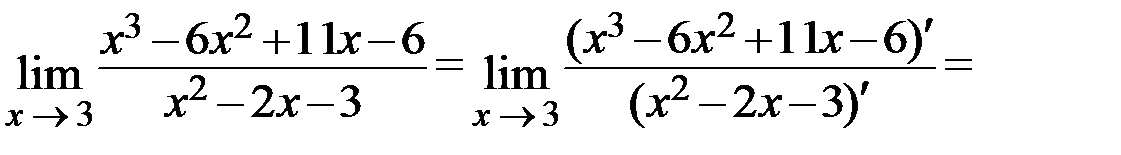
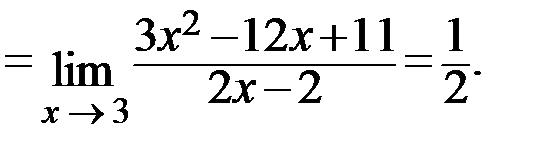
Ответ: 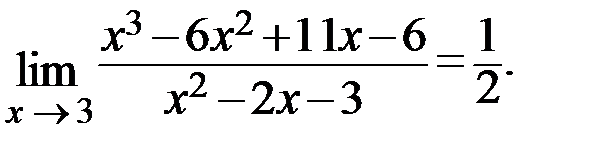
Задание 6. Провести полное исследование функции и построить ее график.
1. 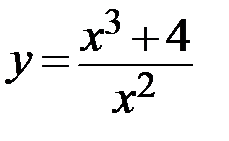 2.
2. 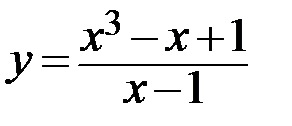 3.
3. 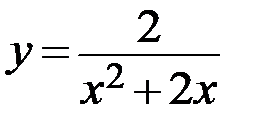
4. 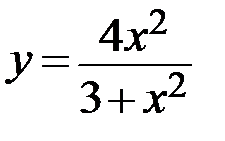 5.
5. 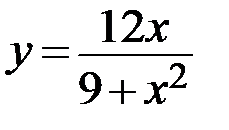 6.
6. 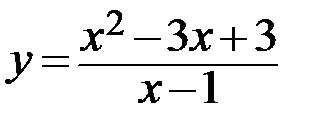
7. 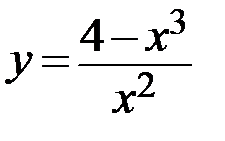 8.
8. 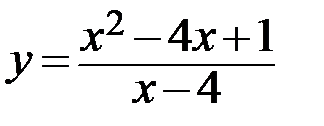 9.
9. 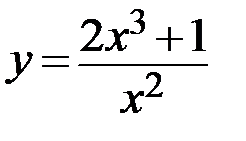
10. 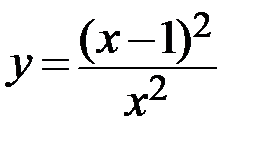 11.
11. 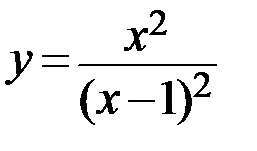 12.
12. 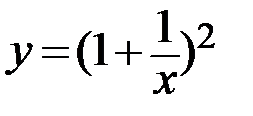
13. 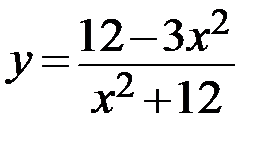 14.
14. 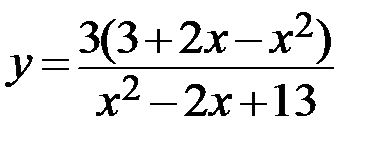 15.
15. 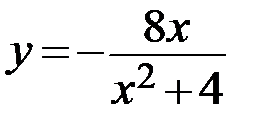
16. 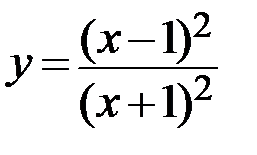 17.
17. 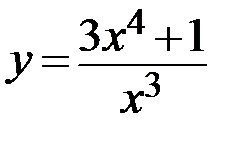 18.
18. 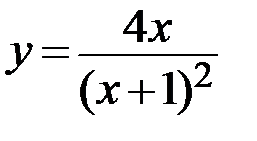
19. 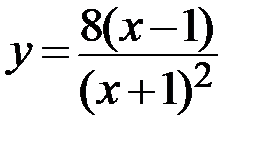 20.
20. 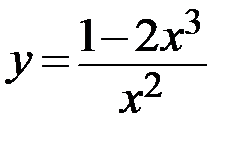 21.
21. 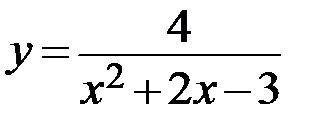
22. 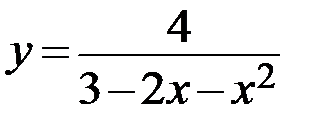 23.
23. 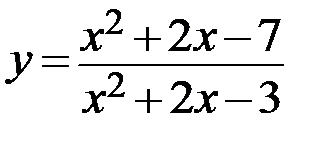 24.
24. 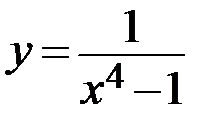
25. 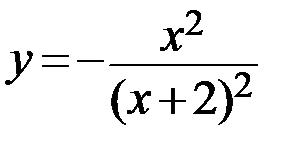 26.
26. 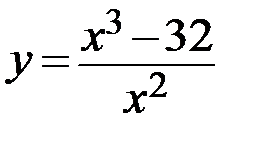 27.
27. 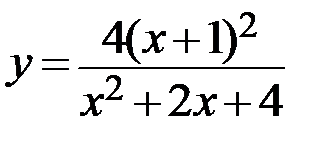
28. 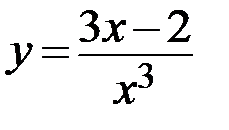 29.
29. 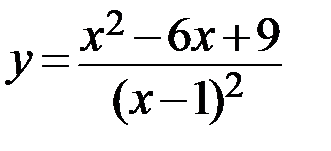 30.
30. 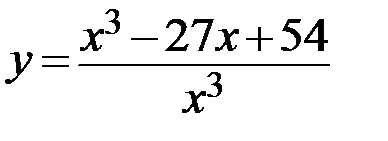
31. 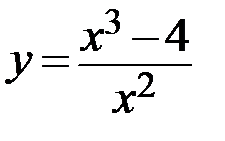 32.
32. 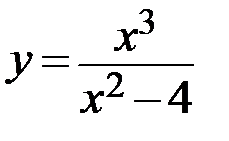
Пример. 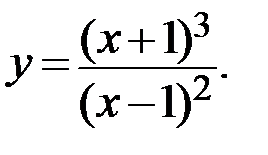
Решение.
Исследование по виду функции.
а) 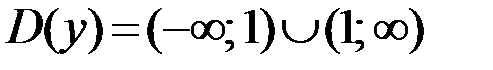 , так как функция определена всюду, кроме точки x=1. В своей области определения функция непрерывна,
, так как функция определена всюду, кроме точки x=1. В своей области определения функция непрерывна, 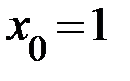 является точкой разрыва графика функции; поведение функции в окрестности этой точки будет рассмотрено ниже.
является точкой разрыва графика функции; поведение функции в окрестности этой точки будет рассмотрено ниже.
б) Функция не является периодической.
в) Так как область определения не симметрична относительно точки x=0, то проверка на чётность и нечётность не проводится. График функции симметрией не обладает.
г) Найдём точки пересечения с осями координат. При x=0 получаем:  то есть (0; 1) – точка пересечения с осью Oy. При y=0 получаем
то есть (0; 1) – точка пересечения с осью Oy. При y=0 получаем 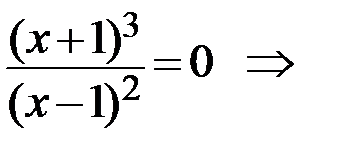 x= –1, то есть (–1; 0) – точка пересечения с осью Ox.
x= –1, то есть (–1; 0) – точка пересечения с осью Ox.
д) Найдём асимптоты графика функции.
Вертикальные асимптоты.
Так как 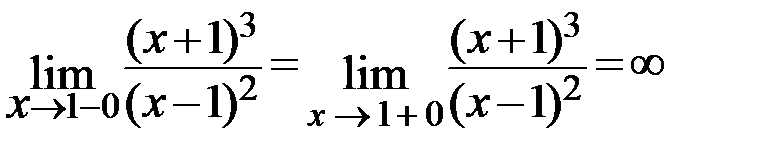 , то
, то 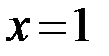 – вертикальная асимптота.
– вертикальная асимптота.
Горизонтальные асимптоты.
Так как 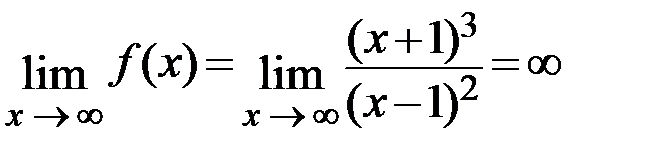 , то горизонтальных асимптот нет.
, то горизонтальных асимптот нет.
Наклонные асимптоты.
Так как 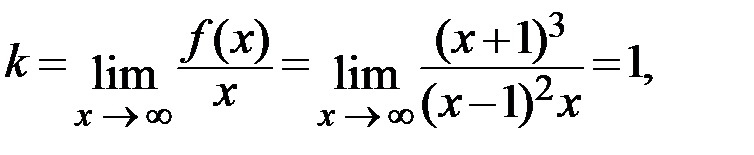
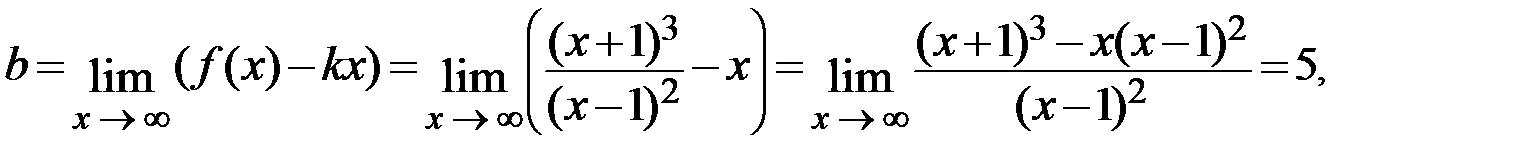 то
то 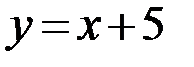 – наклонная асимптота.
– наклонная асимптота.
