Теория возбуждения Ходжкина – Хаксли

В основе данной теории лежит эквивалентная схема замещения мембраны представленная на рисунке 1.4.

Рисунок 1.4 - Эквивалентная схема мембраны Ходжкина - Хаксли

Принимается, что полный ток через мембрану нейрона является суммой емкостного тока , тока за счёт перемещения ионов натрия внутрь клетки , тока за счет перемещения ионов калия из клетки во внеклеточную жидкость , и небольшого тока за счет перемещения ионов других веществ, в частности, ионов хлора . Сопротивления и являются переменными, сопротивление - постоянным, удельная емкость мембраны обозначена через C. , , - равновесные потенциалы мембраны для равной концентрации соответствующих ионов в клетке и внеклеточной среде. Напряжение U определяет потенциал мембраны. Полный ток через мембрану определяется следующей формулой:

(1.1)

Обычно при раздражении клетки при помощи микроэлектрода можно считать, что полный ток через мембрану равен нулю. Тогда потенциал действия (по Ходжкину и Хаксли) определяется дифференциальным уравнением

(1.2)

Ионные токи могут быть выражены через значения проводимостей следующим образом:

(1.3)

где , , , , а - абсолютное значение потенциала покоя.

Ионные проводимости и существенно изменяются при развитии возбуждения. Для того, чтобы описать закон изменения проводимостей , Ходжкин и Хаксли предложили ввести вспомогательную переменную n, подчиняющуюся следующему дифференциальному уравнению:

(1.4)

где - некоторые фиксированные значения, являющиеся функциями деполяризующего напряжения V. Проводимость , тогда может быть записана в виде , где - некоторая константа.

Для параметров и были определены следующие эмпирические зависимости:

Закон изменения проводимости в модели Ходжкина-Хаксли, может быть представлен через решение системы двух дифференциальных уравнений первого порядка

(1.5)

где - постоянные, зависящие от деполяризующего напряжения.

Проводимость представляется функцией этих переменных - , где - некоторая константа.

Были установлены следующие эмпирические зависимости для постоянных уравнений (1.5):

При выводе законов изменения проводимостей мембраны для ионов натрия и калия, внимание в первую очередь обращалось на достижение точного совпадения расчетных и экспериментальных данных.

Как видно из изложенного, теория возбуждения нервной клетки Ходжкина-Хаксли весьма сложна. Рассмотренная теория, уделяя основное внимание мембране нейрона, не рассматривает детально синаптический аппарат, оперируя лишь следствиями его воздействия на мембрану нейрона.

Модель Ижикевича

Данная модель основывается на квадратном полиноме в правой части уравнения для мембранного потенциала, также является двусегментной и содержит дополнительное условие для сброса [1]:

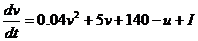
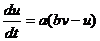
если 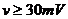, то: ,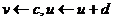

где переменная v отражает потенциал мембраны нейрона, а переменная u отражает переменную восстановления мембраны, которая отвечает за активацию калиевого насоса и дезактивацию натриевого насоса, и обеспечивает обратную связь к v. I - переменная, отражающая синаптические (инъецируемые) токи.

Параметр a описывает временной масштаб переменной восстановления u, чем меньше значение, тем медленнее восстановление. Типовое значения параметра: a=0.02.

Параметр b описывает чувствительность переменной восстановления u к предпороговым колебаниям мембранного потенциала v. Типовое значение b=0.2.

Параметр c описывает значение, до которого сбрасывается мембранный потенциал v после генерации спайка. Типовое значение c=-65mV.

Параметр d описывает сброс переменной восстановления u после генерации спайка. Типовое значение d=2.

В работе [1] показано, что данная модель способна воспроизводить все двадцать типов активности реальных биологических нейронов (по классификации Ижикевича) в зависимости от значений четырех параметров модели.

1.5 Перспективный план исследований

Как было сказано в работе [2] в разработке интеллектуальных систем управления, на базе бионического подхода принципиально важным представляется комплексный подход к решению задачи, т.е. во-первых реализация решения всего спектра задач функционирования робототехнической системы в среде, а не только отдельных частных проблем поддержания устойчивости/хождения/распознавания образов и т.п. И во-вторых на всех уровнях обработки информации от сенсоров к эффекторам робота не допускать сужения контекста. Поскольку представляется затруднительным решение сколь-нибудь сложной задачи полностью, следует попытаться разбить решение полной задачи на этапы таким образом, чтобы на каждом этапе решать упрощенную полную задачу.

Тогда можно выделить следующие этапы в построении системы управления движением робота:

1. Моделирование функционирования отдельных нейронов как простейших СУ, получающих сенсорную информацию и выдающих сигнал управления. Здесь в первую очередь следует провести отработку универсальных алгоритмов настройки нейронов на требуемое поведение (алгоритмы обучения).

2. Моделирование функционирования простейших систем регулирования, обеспечивающих стабилизацию положения объекта с одной кинематической степенью свободы. Позволит провести отработку системы поддержания положения отдельных элементов робота.

3. Моделирование систем регулирования, осуществляющих поддержание положения объекта с одной кинематической степенью свободы по данным, получаемым с гироскопа.

4. Моделирование системы связанного управления пары звеньев манипулятора (смена и удержание положения).

5. Моделирование системы координированного управления несколькими многозвенниками (поддержание устойчивости).

6. Разработка системы управления движением со множеством многозвенников (шагание).

Настоящий отчет посвящен реализации в первую очередь п.3. Пункты 1 и 2 были реализованы ранее.