Перечень графического материала (с точным указанием обязательных чертежей)

нет

Консультанты по проекту (с указанием относящихся к ним разделов работы)

7 Дата выдачи задания11.09.2013 г

Руководительвед. программист А.В.Бахшиев

Задание принял к исполнению

(дата)

(подпись студента)

СОДЕРЖАНИЕ

ВВЕДЕНИЕ. 5

1 Анализ проблемы.. 6

1.1 Искусственные нейроны.. 6

1.2 Модели биологических нейронов. 10

1.3 Теория возбуждения Ходжкина – Хаксли. 12

1.4 Модель Ижикевича. 14

1.5 Перспективный план исследований. 15

2 Разработка математических моделей. 18

2.1 Описание исследуемой системы.. 18

2.2 Модель нейрона с взаимным влиянием ионных механизмов друг на друга 20

2.3 Модель регулятора со структурной адаптацией. 23

2.4 Модель гироскопа. 24

2.5 Выводы.. 26

3 Разработка компьютерных моделей. 28

3.1 Средства моделирования. 28

3.2 Реализация алгоритма одновременного влияния синапсов на все ионные механизмы нейрона. 36

3.3 Модель регулятора. 37

3.4 Модель гироскопа. 41

3.5 Модель исследуемой системы.. 42

3.6 Алгоритм адаптации структуры НС регулятора. 43

3.7 Выводы.. 45

4 Исследования. 46

4.1 Исследование поведения нейрона с взаимным влиянием ионных механизмов нейрона. 46

4.2 Исследование работы нейросетевого регулятора в задаче поддержания положения обратного маятника при наличии перекрестных связей между ионными механизмами нейрона. 52

4.3 План дальнейших исследований. 54

4.4 Выводы.. 55

Заключение. 55

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ.. 57

ВВЕДЕНИЕ

Последние десятилетия характеризуются возрастанием интереса к исследованиям мозга, что связано, с одной стороны, с появлением более совершенной исследовательской аппаратуры и методик, а с другой – с увеличением роли бионики в решении проблем искусственного интеллекта. Предыдущие работы помогли осознать основную трудность подобного рода исследований, - это большая сложность изучаемого объекта, и методическая необходимость в системном подходе к проблеме на основе интегрирования результатов, полученных в философии, биологии, психологии, вычислительной техники.

Так как объект исследований ограничивает возможности широкомасштабных физических экспериментов непосредственно на нем, возникает необходимость в имитационном моделировании и, соответствующем согласовании создаваемых моделей с теорией вычислений.

Все больше внимания, которое уделяется решению проблем построения систем управления динамическими объектами и систем обработки информации, на основе биологического подхода, связано с тем, что большой класс задач управления и обработки данных плохо решается традиционными методами, требуя больших временных и финансовых затрат. Задачи данного класса, как правило, плохо формализуемы и не имеют точных математических моделей. Поэтому, ведущая роль в решении подобных задач принадлежит нейрокибернетике.

На сегодняшний день уже существует множество реально действующих технических вычислительных нейронных сетей, структура которых подобна участкам биологической нервной системы. В целом, подобные сети применяются для решения таких задач как:

· распознавание изображений и речи;

· задачи экстраполяции функций, например, прогнозирование курсов валют и т.п.;

· адаптивное управление движением;

· аппроксимация функционалов.

Несмотря на наличие определенных успехов в моделировании функций нервной системы, теория нейронных сетей еще лишь зарождается. Модели нейронов и нейронных сетей, лежащие в основе современных нейрокомпьютеров весьма упрощены, и не отражают поведение естественных нейронных структур. Совместные достижения нейрофизиологии и морфологии выявили основные функции нейронных образований различных областей мозга и организацию связей внутри этих образований. Однако принципы передачи и обработки сигналов в таких структурах остаются гипотетическими, так как выявленная структура связей в большинстве случаев чрезвычайно сложна и пока не поддаётся анализу.

Нейронная сеть является распределённой структурой с множеством входов и параллельной обработкой информации. Основным функциональным элементом как естественной, так и искусственной нейронной сети является нейрон – объект с множеством входов и одним выходом, осуществляющий сложное преобразование входных сигналов в выходной сигнал.

Анализ проблемы

Искусственные нейроны

Считается, что теория нейронных сетей, как научное направление, впервые была обозначена в классической работе Мак-Каллока и Питтса 1943 г. В ней утверждалось, что, в принципе, любую арифметическую или логическую функцию можно реализовать с помощью простой нейронной сети. Эта работа считается первым систематическим изучением искусственных нейронных сетей. Позднее в своих работах они исследовали сети для распознавания изображений, подвергаемых сдвигам и поворотам. Простая нейронная модель, использовалась в большей части их работ. МакКаллок и Питтс предложили в качестве модели искусственного нейрона использовать бинарный пороговый элемент. Такой нейрон вычисляет взвешенную сумму n входных сигналов x_j, j = 1, 2... n, и формирует на выходе сигнал, равный 1, если эта сумма превышает определенный порог u, и 0 - в противном случае.

Часто удобно рассматривать u как весовой коэффициент, связанный с постоянным входом x₀ = 1. Положительные веса соответствуют возбуждающим связям, а отрицательные - тормозным. МакКаллок и Питтс доказали, что при соответствующим образом подобранных весах совокупность параллельно функционирующих нейронов подобного типа способна выполнять универсальные вычисления.

Предложенная модель нейрона в дальнейшем претерпела некоторые изменения и получила название искусственного нейрона. Искусственный нейрон, имитируя в первом приближении свойства биологического нейрона, характеризуется своим текущим состоянием по аналогии с нервными клетками головного мозга, которые могут быть возбуждены или заторможены. Он обладает группой синапсов – однонаправленных входных связей, соединенных с выходами других нейронов, а также имеет аксон – выходную связь данного нейрона, по которой сигнал (возбуждения или торможения) поступает на синапсы следующих нейронов. Общий вид искусственного нейрона приведен на рисунке 1.1.

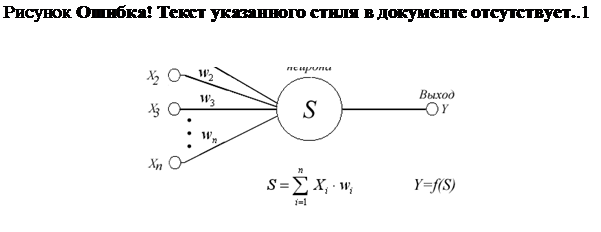
Каждый синапс характеризуется величиной синаптической связи или ее весом w_i, который по физическому смыслу эквивалентен электрической проводимости.

Текущее состояние нейрона определяется, как взвешенная сумма его входов: 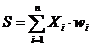. Выход нейрона есть функция его состояния Y= f(S).

Нелинейная функция f называется активационной и может иметь различный вид (Рисунок 1.2). Одной из наиболее распространенных является нелинейная функция с насыщением, так называемая логистическая функция или сигмоид .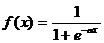

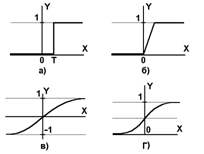
Рисунок 1.2 - Варианты активационной функции искусственного нейрона:

а) функция единичного скачка; б) линейный порог; в) гиперболический тангенс;

г) сигмоид.

При уменьшении a сигмоид становится более пологим, в пределе при a=0 вырождаясь в горизонтальную линию на уровне 0.5, при увеличении a сигмоид приближается по внешнему виду к функции единичного скачка с порогом T в точке x=0. Из выражения для сигмоида очевидно, что выходное значение нейрона лежит в диапазоне [0, 1].

Активационную функцию можно считать нелинейной усилительной характеристикой искусственного нейрона. Коэффициент усиления вычисляется как отношение приращения величины y к вызвавшему его небольшому приращению величины s. Он выражается наклоном кривой при определенном уровне возбуждения и, в случае сигмоидной функции, изменяется от малых значений при больших отрицательных возбуждениях (кривая почти горизонтальна), до максимального значения при нулевом возбуждении и снова уменьшается, когда возбуждение становится большим положительным. Таким образом, сигмоидная функция обладает свойством усиливать слабые сигналы лучше, чем большие, и предотвращает насыщение от больших сигналов, так как они соответствуют областям аргументов, где сигмоид имеет пологий наклон.

Для придания нейронным сетям, создаваемым из совокупностей описанных выше искусственных нейронов, желаемых свойств, нейронам сети придают дополнительные возможности. Главным здесь является возможность изменения весов входов, во время работы сети по некоторым правилам (законам обучения). Таким образом, веса входов могут быть: 1) постоянными коэффициентами, 2) управляемыми, 3) перестраивающимися в зависимости от входного по данному каналу сигнала, 4) коэффициентами типа синапсов Хебба, изменяющимися под влиянием выходного сигнала нейрона.

В некоторых случаях помимо настройки весов входов, также используют изменение параметров активационной функции.

Рассмотренная модель искусственного нейрона игнорирует многие свойства своего биологического прототипа. Например, она не учитывает задержки во времени, которые влияют на динамику системы. Входные сигналы сразу же порождают выходной сигнал. Другим важным отличием является необходимость модификации весов входов для получения желаемого поведения. В естественном нейроне веса отдельных синапсов (входов) фиксированы и не могут быстро меняться, а вклад каждого входа изменяется в зависимости от общего количества активных в текущий момент времени входов. Следствием утраты этих свойств естественного нейрона является необходимость введения правил обучения для придания нейрону и нейронной сети требуемых пластических свойств, связанных с возможностью обучения. Предложенная модель также не способна воспроизводить свойства абсолютной и относительной рефрактерности, являющиеся существенными свойствами реального нейрона.