О научно-исследовательской работе

ОТЧЕТ

О научно-исследовательской работе

Тема: Исследование динамических характеристик модели естественного нейрона в задачах управления звеном манипулятора

Выполнил студент группы 43328/2	__________ Ф.В. Гунделах
Руководитель работы	__________ А.В. Бахшиев

Санкт-Петербург, 2013

САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

ИНСТИТУТ МЕТАЛЛУРГИИ МАШИНОСТРОЕНИЯ И ТРАНСПОРТА

ОТДЕЛЕНИЕ ТЕХНОЛОГИЙ МАШИНОСТРОЕНИЯ

Кафедра «Мехатроника и роботостроение» (при ЦНИИ РТК)

УТВЕРЖДАЮ

Зав. кафедрой

______________А.В.Лопота

«____»____________2013 г.

ЗАДАНИЕ

на научно-исследовательскую работу

Гунделах Филиппу Викторовичу

студенту гр. 43328/2

Тема проекта (работы)

Исследование динамических характеристик модели естественного нейрона в задачах управления звеном манипулятора

2 Срок сдачи студентом законченного проекта (работы)

Исходные данные к проекту (работе)

Среда моделирования нейронных сетей NMSDK

Содержание расчетно-пояснительной записки

1. Анализ проблемы

2. Разработка математических моделей

3. Разработка компьютерных моделей

4. Исследования

Перечень графического материала (с точным указанием обязательных чертежей)

нет

Консультанты по проекту (с указанием относящихся к ним разделов работы)

7 Дата выдачи задания11.09.2013 г

Руководительвед. программист А.В.Бахшиев

Задание принял к исполнению

(дата)

(подпись студента)

СОДЕРЖАНИЕ

ВВЕДЕНИЕ. 5

1 Анализ проблемы.. 6

1.1 Искусственные нейроны.. 6

1.2 Модели биологических нейронов. 10

1.3 Теория возбуждения Ходжкина – Хаксли. 12

1.4 Модель Ижикевича. 14

1.5 Перспективный план исследований. 15

2 Разработка математических моделей. 18

2.1 Описание исследуемой системы.. 18

2.2 Модель нейрона с взаимным влиянием ионных механизмов друг на друга 20

2.3 Модель регулятора со структурной адаптацией. 23

2.4 Модель гироскопа. 24

2.5 Выводы.. 26

3 Разработка компьютерных моделей. 28

3.1 Средства моделирования. 28

3.2 Реализация алгоритма одновременного влияния синапсов на все ионные механизмы нейрона. 36

3.3 Модель регулятора. 37

3.4 Модель гироскопа. 41

3.5 Модель исследуемой системы.. 42

3.6 Алгоритм адаптации структуры НС регулятора. 43

3.7 Выводы.. 45

4 Исследования. 46

4.1 Исследование поведения нейрона с взаимным влиянием ионных механизмов нейрона. 46

4.2 Исследование работы нейросетевого регулятора в задаче поддержания положения обратного маятника при наличии перекрестных связей между ионными механизмами нейрона. 52

4.3 План дальнейших исследований. 54

4.4 Выводы.. 55

Заключение. 55

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ.. 57

ВВЕДЕНИЕ

Последние десятилетия характеризуются возрастанием интереса к исследованиям мозга, что связано, с одной стороны, с появлением более совершенной исследовательской аппаратуры и методик, а с другой – с увеличением роли бионики в решении проблем искусственного интеллекта. Предыдущие работы помогли осознать основную трудность подобного рода исследований, - это большая сложность изучаемого объекта, и методическая необходимость в системном подходе к проблеме на основе интегрирования результатов, полученных в философии, биологии, психологии, вычислительной техники.

Так как объект исследований ограничивает возможности широкомасштабных физических экспериментов непосредственно на нем, возникает необходимость в имитационном моделировании и, соответствующем согласовании создаваемых моделей с теорией вычислений.

Все больше внимания, которое уделяется решению проблем построения систем управления динамическими объектами и систем обработки информации, на основе биологического подхода, связано с тем, что большой класс задач управления и обработки данных плохо решается традиционными методами, требуя больших временных и финансовых затрат. Задачи данного класса, как правило, плохо формализуемы и не имеют точных математических моделей. Поэтому, ведущая роль в решении подобных задач принадлежит нейрокибернетике.

На сегодняшний день уже существует множество реально действующих технических вычислительных нейронных сетей, структура которых подобна участкам биологической нервной системы. В целом, подобные сети применяются для решения таких задач как:

· распознавание изображений и речи;

· задачи экстраполяции функций, например, прогнозирование курсов валют и т.п.;

· адаптивное управление движением;

· аппроксимация функционалов.

Несмотря на наличие определенных успехов в моделировании функций нервной системы, теория нейронных сетей еще лишь зарождается. Модели нейронов и нейронных сетей, лежащие в основе современных нейрокомпьютеров весьма упрощены, и не отражают поведение естественных нейронных структур. Совместные достижения нейрофизиологии и морфологии выявили основные функции нейронных образований различных областей мозга и организацию связей внутри этих образований. Однако принципы передачи и обработки сигналов в таких структурах остаются гипотетическими, так как выявленная структура связей в большинстве случаев чрезвычайно сложна и пока не поддаётся анализу.

Нейронная сеть является распределённой структурой с множеством входов и параллельной обработкой информации. Основным функциональным элементом как естественной, так и искусственной нейронной сети является нейрон – объект с множеством входов и одним выходом, осуществляющий сложное преобразование входных сигналов в выходной сигнал.

Анализ проблемы

Искусственные нейроны

Считается, что теория нейронных сетей, как научное направление, впервые была обозначена в классической работе Мак-Каллока и Питтса 1943 г. В ней утверждалось, что, в принципе, любую арифметическую или логическую функцию можно реализовать с помощью простой нейронной сети. Эта работа считается первым систематическим изучением искусственных нейронных сетей. Позднее в своих работах они исследовали сети для распознавания изображений, подвергаемых сдвигам и поворотам. Простая нейронная модель, использовалась в большей части их работ. МакКаллок и Питтс предложили в качестве модели искусственного нейрона использовать бинарный пороговый элемент. Такой нейрон вычисляет взвешенную сумму n входных сигналов x_j, j = 1, 2... n, и формирует на выходе сигнал, равный 1, если эта сумма превышает определенный порог u, и 0 - в противном случае.

Часто удобно рассматривать u как весовой коэффициент, связанный с постоянным входом x₀ = 1. Положительные веса соответствуют возбуждающим связям, а отрицательные - тормозным. МакКаллок и Питтс доказали, что при соответствующим образом подобранных весах совокупность параллельно функционирующих нейронов подобного типа способна выполнять универсальные вычисления.

Предложенная модель нейрона в дальнейшем претерпела некоторые изменения и получила название искусственного нейрона. Искусственный нейрон, имитируя в первом приближении свойства биологического нейрона, характеризуется своим текущим состоянием по аналогии с нервными клетками головного мозга, которые могут быть возбуждены или заторможены. Он обладает группой синапсов – однонаправленных входных связей, соединенных с выходами других нейронов, а также имеет аксон – выходную связь данного нейрона, по которой сигнал (возбуждения или торможения) поступает на синапсы следующих нейронов. Общий вид искусственного нейрона приведен на рисунке 1.1.

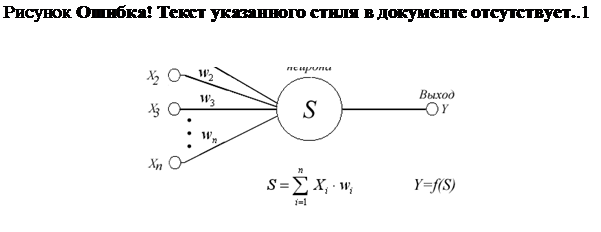
Каждый синапс характеризуется величиной синаптической связи или ее весом w_i, который по физическому смыслу эквивалентен электрической проводимости.

Текущее состояние нейрона определяется, как взвешенная сумма его входов: 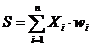. Выход нейрона есть функция его состояния Y= f(S).

Нелинейная функция f называется активационной и может иметь различный вид (Рисунок 1.2). Одной из наиболее распространенных является нелинейная функция с насыщением, так называемая логистическая функция или сигмоид .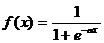

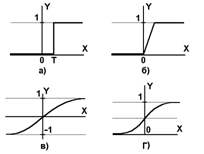
Рисунок 1.2 - Варианты активационной функции искусственного нейрона:

а) функция единичного скачка; б) линейный порог; в) гиперболический тангенс;

г) сигмоид.

При уменьшении a сигмоид становится более пологим, в пределе при a=0 вырождаясь в горизонтальную линию на уровне 0.5, при увеличении a сигмоид приближается по внешнему виду к функции единичного скачка с порогом T в точке x=0. Из выражения для сигмоида очевидно, что выходное значение нейрона лежит в диапазоне [0, 1].

Активационную функцию можно считать нелинейной усилительной характеристикой искусственного нейрона. Коэффициент усиления вычисляется как отношение приращения величины y к вызвавшему его небольшому приращению величины s. Он выражается наклоном кривой при определенном уровне возбуждения и, в случае сигмоидной функции, изменяется от малых значений при больших отрицательных возбуждениях (кривая почти горизонтальна), до максимального значения при нулевом возбуждении и снова уменьшается, когда возбуждение становится большим положительным. Таким образом, сигмоидная функция обладает свойством усиливать слабые сигналы лучше, чем большие, и предотвращает насыщение от больших сигналов, так как они соответствуют областям аргументов, где сигмоид имеет пологий наклон.

Для придания нейронным сетям, создаваемым из совокупностей описанных выше искусственных нейронов, желаемых свойств, нейронам сети придают дополнительные возможности. Главным здесь является возможность изменения весов входов, во время работы сети по некоторым правилам (законам обучения). Таким образом, веса входов могут быть: 1) постоянными коэффициентами, 2) управляемыми, 3) перестраивающимися в зависимости от входного по данному каналу сигнала, 4) коэффициентами типа синапсов Хебба, изменяющимися под влиянием выходного сигнала нейрона.

В некоторых случаях помимо настройки весов входов, также используют изменение параметров активационной функции.

Рассмотренная модель искусственного нейрона игнорирует многие свойства своего биологического прототипа. Например, она не учитывает задержки во времени, которые влияют на динамику системы. Входные сигналы сразу же порождают выходной сигнал. Другим важным отличием является необходимость модификации весов входов для получения желаемого поведения. В естественном нейроне веса отдельных синапсов (входов) фиксированы и не могут быстро меняться, а вклад каждого входа изменяется в зависимости от общего количества активных в текущий момент времени входов. Следствием утраты этих свойств естественного нейрона является необходимость введения правил обучения для придания нейрону и нейронной сети требуемых пластических свойств, связанных с возможностью обучения. Предложенная модель также не способна воспроизводить свойства абсолютной и относительной рефрактерности, являющиеся существенными свойствами реального нейрона.

Модель Ижикевича

Данная модель основывается на квадратном полиноме в правой части уравнения для мембранного потенциала, также является двусегментной и содержит дополнительное условие для сброса [1]:

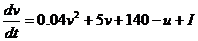
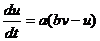
если 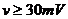, то: ,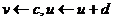

где переменная v отражает потенциал мембраны нейрона, а переменная u отражает переменную восстановления мембраны, которая отвечает за активацию калиевого насоса и дезактивацию натриевого насоса, и обеспечивает обратную связь к v. I - переменная, отражающая синаптические (инъецируемые) токи.

Параметр a описывает временной масштаб переменной восстановления u, чем меньше значение, тем медленнее восстановление. Типовое значения параметра: a=0.02.

Параметр b описывает чувствительность переменной восстановления u к предпороговым колебаниям мембранного потенциала v. Типовое значение b=0.2.

Параметр c описывает значение, до которого сбрасывается мембранный потенциал v после генерации спайка. Типовое значение c=-65mV.

Параметр d описывает сброс переменной восстановления u после генерации спайка. Типовое значение d=2.

В работе [1] показано, что данная модель способна воспроизводить все двадцать типов активности реальных биологических нейронов (по классификации Ижикевича) в зависимости от значений четырех параметров модели.

1.5 Перспективный план исследований

Как было сказано в работе [2] в разработке интеллектуальных систем управления, на базе бионического подхода принципиально важным представляется комплексный подход к решению задачи, т.е. во-первых реализация решения всего спектра задач функционирования робототехнической системы в среде, а не только отдельных частных проблем поддержания устойчивости/хождения/распознавания образов и т.п. И во-вторых на всех уровнях обработки информации от сенсоров к эффекторам робота не допускать сужения контекста. Поскольку представляется затруднительным решение сколь-нибудь сложной задачи полностью, следует попытаться разбить решение полной задачи на этапы таким образом, чтобы на каждом этапе решать упрощенную полную задачу.

Тогда можно выделить следующие этапы в построении системы управления движением робота:

1. Моделирование функционирования отдельных нейронов как простейших СУ, получающих сенсорную информацию и выдающих сигнал управления. Здесь в первую очередь следует провести отработку универсальных алгоритмов настройки нейронов на требуемое поведение (алгоритмы обучения).

2. Моделирование функционирования простейших систем регулирования, обеспечивающих стабилизацию положения объекта с одной кинематической степенью свободы. Позволит провести отработку системы поддержания положения отдельных элементов робота.

3. Моделирование систем регулирования, осуществляющих поддержание положения объекта с одной кинематической степенью свободы по данным, получаемым с гироскопа.

4. Моделирование системы связанного управления пары звеньев манипулятора (смена и удержание положения).

5. Моделирование системы координированного управления несколькими многозвенниками (поддержание устойчивости).

6. Разработка системы управления движением со множеством многозвенников (шагание).

Настоящий отчет посвящен реализации в первую очередь п.3. Пункты 1 и 2 были реализованы ранее.

Модель гироскопа

Упрощённое математическое описание гироскопа (без блока насыщения, случайных шумов и без учёта возможных ускорений вдоль осей) можно представить следующим образом (верхний индекс в скобках – производная по времени):

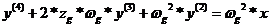
где x - входной момент;

y - угол на выходе;

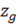- коэффициент демпфирования;

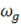- собственная частота гироскопа.

Реакция гироскопа на постоянное входное воздействие представлена на Рисунок 2.5, а реакция на единичное входное воздействие на Рисунок 2.6

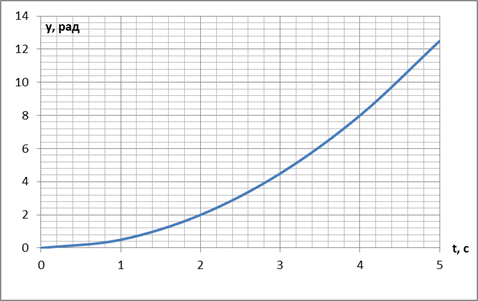
Рисунок 2.5 - Реакция гироскопа на постоянное входное воздействие

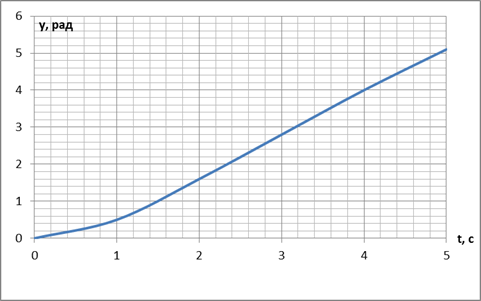
Рисунок 2.6 - Реакция гироскопа на единичное входное воздействие

Увеличение коэффициента демпфирования z_g 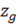приводит к уменьшению скорости нарастания угла на выходе, таким же образом на системе сказывается и уменьшение собственной частоты ω_g 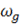, что можно наглядно пронаблюдать на приведенных ниже графиках (Рисунок 2.7, Рисунок 2.8).

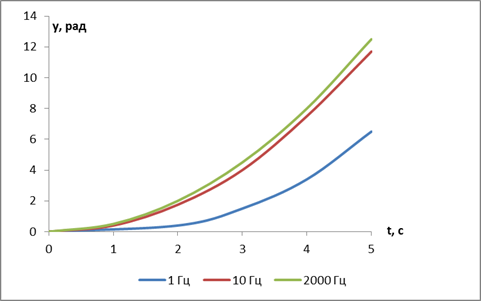
Рисунок 2.7 - Зависимость угла на выходе от собственной частоты ω_g

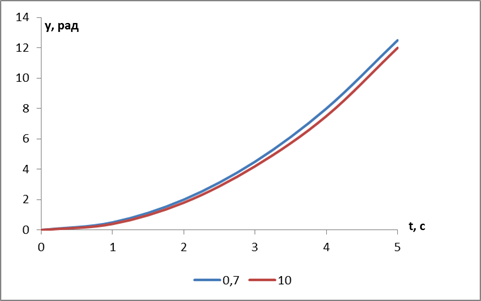
Рисунок 2.8 - Зависимость угла на выходе гироскопа от коэффициента демпфирования z_g

Выводы

Была модифицирована модель ионного механизма нейрона и улучшены динамические характеристики модели нейрона.

Предложено описание исследуемой системы в целом и модели гироскопа, а также модель регулятора со структурной адаптацией.

Рассмотрены типовые реакции модели гироскопа.

Средства моделирования

Для компьютерного моделирования была использована библиотека NMSDK (Neuro Modeler Software Developer Kit) [7]. Подробное описание библиотеки приведено в [1].

Библиотека позволяет пользователю:

- формировать исследуемую модель из набора готовых компонент, описывающих отдельные алгоритмы, произвольным образом конфигурируя выбранные компоненты и связи между ними;

- управлять параметрами и переменными состояния компонент через универсальный интерфейс;

- Запоминать для повторного использования собранную модель;

- Наблюдать значения выходов компонент на графиках.

Отдельные компоненты библиотеки предоставляют возможности для:

- сохранения данных расчетов в таблицы для дальнейшего анализа в сторонних системах;

- съема данных с датчиков и управления внешними системами, такими как манипуляторы.

Список компонент может легко пополняться программистом для расширения возможностей библиотеки.

Также интерфейсное ПО библиотеки может функционировать в качестве сервера, позволяющего:

- проводить расчет модели в пошаговом режиме, или в режиме реального времени (при достаточных вычислительных ресурсах);

- принимать команды внешнего управления в формате XML по протоколу TCP, в частности команды на запуск/останов расчет, и сброс модели в исходное состояние;

- передавать результаты расчетов удаленному приемнику в формате XML по протоколу TCP.

Ниже представлено описание пользовательского интерфейса библиотеки.

После запуска ПО открывается окно, представленное на рисунке ниже (Рисунок 3.1).

Для открытия существующего проекта, необходимо выбрать пункт меню File->Load Project, и выбрать необходимый файл проекта. После загрузки проекта, главное окно приложения примет следующий вид (Рисунок 3.2). На этом рисунке:

1 Панель инструментов.

2 Панель переключения между рабочими окнами интерфейса.

3 Список компонент модели.

4 Список параметров выбранного компонента.

5 Журнал событий и оценка производительности алгоритмов.

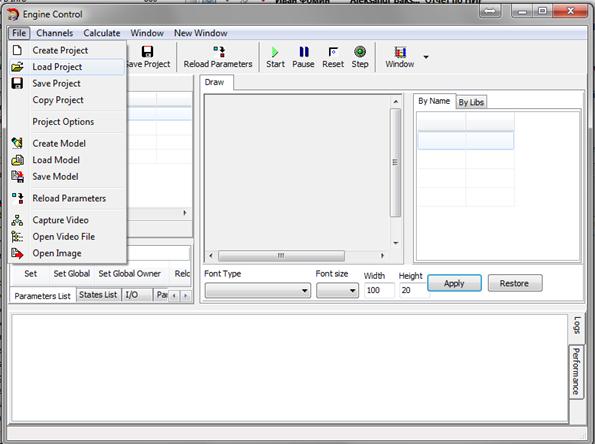
Рисунок 3.1 – Вид главного окна интерфейса при запуске приложения

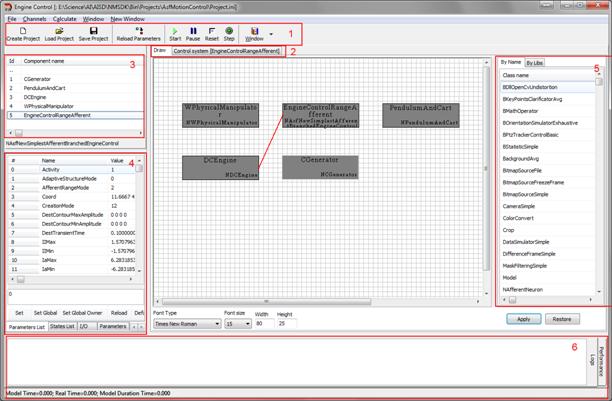
Рисунок 3.2 – Общий вид главного окна интерфейса после открытия проекта

В панели инструментов наиболее часть используются кнопки, дублирующие функциональность пункта главного меню Calculate. Эти кнопки позволяют

- запустить расчет (Start);

- приостановить расчет (Pause);

- сбросить модель в нулевое состояние (Reset);

- провести одну итерацию расчета (Step).

Для управления параметрами компонент, или просмотром текущих значений переменных состояния следует воспользоваться группой элементов 3 и 4 (Рисунок 3.2). В элементе 3 можно выбрать требуемый компонент, а ниже в 4 просмотреть его параметры (вкладки внизу элемента 4 – Parameters List или Parameters), переменные состояния (вкладки States List или States), список входов и выходов (вкладка IO). При необходимости изменить значения параметра, или переменной состояния, необходимо, например в Parameters List выбрать в списке значение требуемого параметра, в поле ввода под списком ввести требуемое значение, и нажать кнопку Set ниже.

Кнопка Set Global, расположенная рядом, изменит значения всех параметров с таким именем во всех компонентах модели.

Кнопка Set Global Owner – изменит значения всех параметров с таким именем во всех компонентах, у которых владелец совпадает по типу с владельцем модифицируемого компонента, и перед этим запросит имя компонента, среди дочерних компонент которого следует производить поиск для замены.

Кнопка Reload – обновляет список актуальными значениями.

Кнопка Default – сбрасывает значения всех параметров выбранного компонента в значения по умолчанию.

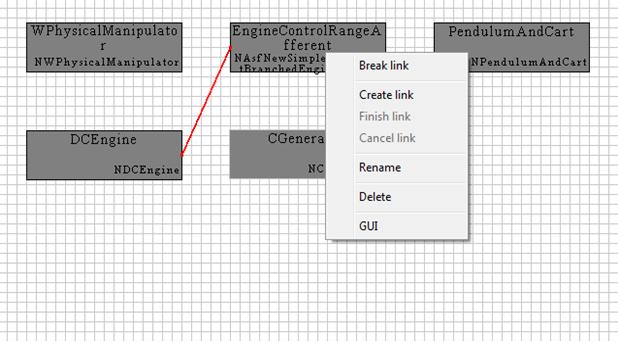
Рисунок 3.3 – Меню управления компонентом модели

По умолчанию в интерфейсе открывается рабочее окно Draw. В этом окне можно управлять структурой компонент модели, и связями между ними. Каждый компонент в этом окне представлен отдельным прямоугольником с текстом, где верхняя строка – это имя компонента в рамках его родителя, а нижняя строка – имя прототипа компонента в коллекции (см элемент 5 главного окна).

Удерживая левую кнопку мыши можно перемещать прямоугольник, описывающий компонент. Двойной щелчок левой кнопкой мыши по прямоугольнику обеспечит переход внутрь (на уровень вниз), а двойной щелчок правой кнопкой – переход наружу (на уровень вверх).

На рисунке выше (Рисунок 3.3) показано меню управления компонентом в рабочем окне Draw. Здесь:

- Break link – разрывает существующую связь выбранного компонента, предварительно отображая окно с доступными связями (Рисунок 3.4);

- Create/Finish/Cancel link – создает новую связь. Для создания связи необходимо выделить компонент-источник связи, и выбрать на нем пункт меню Create link, затем переместиться на компонент-приемник связи (допускается перемещение между уровнями) и завершить формирование связи, выбрав кнопку Finish link. В любой момент можно выбрать пункт меню Cancel link и отменить создание связи. При завершении формирования связи будет открыто окно (Рисунок 3.5) в котором в левой части можно будет выбрать номер выхода компонента-источника, а в правой части номер входа компонента-приемника, или одного из его дочерних компонент. При выборе номера входа с индексом равным -1, будет предпринята попытка создать в соответствующем компоненте новый вход и подключиться к нему.

- Rename – открывает окно смени имени компонента;

- Delete – удаляет компонент из модели, разрывая все существующие связи с ним;

- GUI – Отображает в рабочей области вкладку с интерфейсом управления этим компонентом, если таковой доступен (например см. Рисунок 3.6).

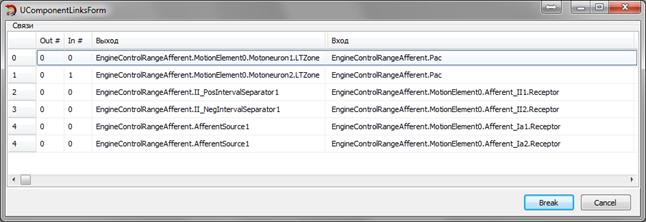
Рисунок 3.4 – Окно уничтожения существующей связи между компонентами

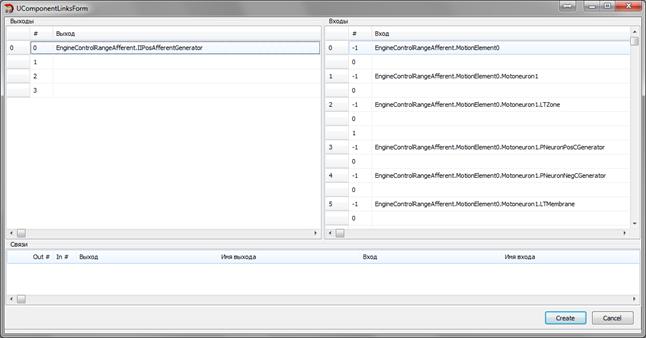
Рисунок 3.5 – Окно создания новой связи между компонентами

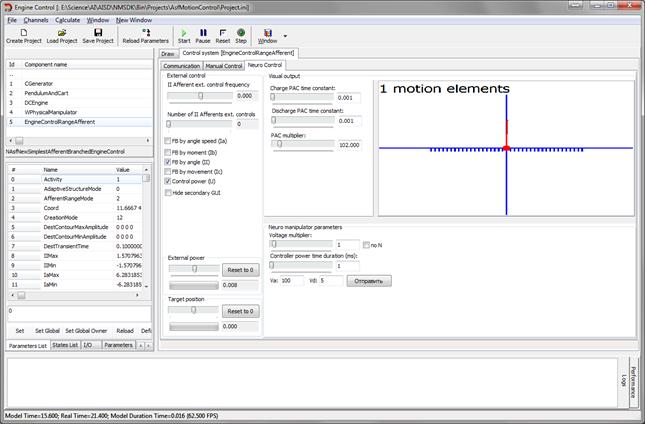
Рисунок 3.6 – Интерфейс управления компонентом нейросетевого регулятора

На следующем рисунке (Рисунок 3.7) показано окно отображения графиков сигналов компонент модели. Чтобы открыть это окно, необходимо в главном меню приложения выбрать пункт Window->Watch Window. В этом окне можно создавать произвольное количество вкладок с графиками, на каждой из которых может быть произвольное число графиков. Для добавления новой вкладки или удаления текущей, необходимо навести мышь на имя любой существующей вкладки, открыть контекстное меню и выбрать соответствующее действие.

Для управления графиками в текущей вкладке, необходимо в любом месте графика открыть контекстное меню, как показано на рисунке (Рисунок 3.7).

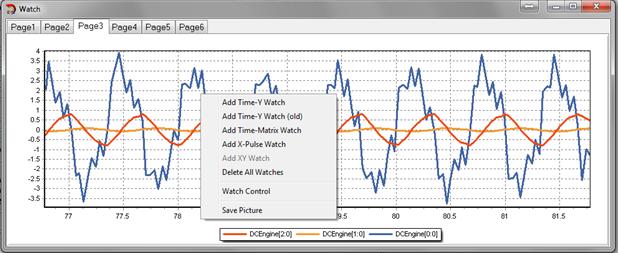
Рисунок 3.7 – Окно отображения графиков сигналов компонент модели

Уже существующие графики можно корректировать выбрав из показанного выше меню пункт Watch Control, при этом откроется следующее окно (Рисунок 3.8).

В этом окне можно выбрать подпись какие графики следует скрыть, подписи к каждому графику, а также его цвет, тип и толщину линии, подписи осей и временной интервал, на котором будет отображаться график.

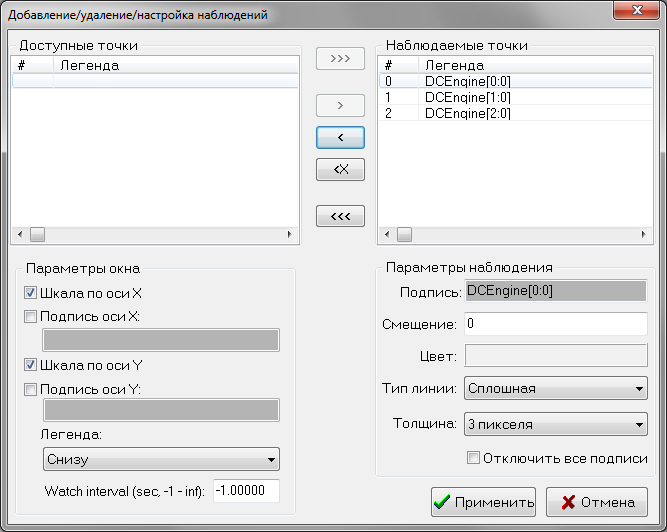
Рисунок 3.8 – Окно управления выбранными графиками

Модель регулятора

Класс регулятора, реализующего схему, представленную выше (Рисунок 2.2), реализован в коллекции Libraries/MotionControlLib среды NMSDK. Имя модуля NEngineMotionControl. В модуле описан одноименный класс, интерфейс которого описан ниже.

Параметры класса представлены в таблице (Таблица 3.2).

Таблица 3.2 – Параметры класса NEngineMotionControl

Имя параметра	Тип	Описание
NumMotionElements	size_t	Число управляющих элементов
CreationMode	int	Режим формирования сети 0 - Signum 1 - Range 2 - Branched Range 3 - Branched Range Crosslinks 4 - Branched Ind. Range 5 - Branched Ind. Range Crosslinks 10 - Branched Ind. Range Continues LTZone neurons 11 - Simplest 2 neuron model 12 - As 11 but speed and force control added
MotionElementClassName	NameT	Имя класса управляющего элемента
AdaptiveStructureMode	int	Режим включения адаптивной перестройки структуры 0 - нет адаптивности 1 - адаптивность включена с полным сбрсом управления 2 - включена автоматическая адаптация c полным сбросом управления
IaMin, IaMax	double	Диапазон афферентных нейронов по каналу Ia
IbMin, IbMax	double	Диапазон афферентных нейронов по каналу Ib
IIMin, IIMax	double	Диапазон афферентных нейронов по каналу II
IcMin, IcMax	double	Диапазон афферентных нейронов по каналу Ic
PacGain	double	Максимальное усиление управляющего воздействия 0 - Разбиение на диапазоны [Max/(i+1)] где i - индекс диапазона 1 - Разбиение на диапазоны [Max/(i+1)] где i - индекс диапазона 2 - 3 - Max/(N-i), где i - индекс диапазона, а N - число диапазонов
AfferentRangeMode	int	Режим настройки диапазонов афферентных нейронов 0 - диапазоны одинаковой длины 1 - диапазоны с удвоением длины, и минимальной шириной в процентах MinAfferentRange от соответствующей разницы *Max-*Min
PacRangeMode	int	Режим настрйоки диапазонов PAC
DestContourMaxAmplitude	std::vector<double>	Маскимально допустимая амплитуда колебаний
DestContourMinAmplitude	std::vector<double>	Минимально допустимая амплитуда колебаний
DestTransientTime	double	Желаемое время переходного процесса
UseContourData	std::vector<bool>	Используемые в адаптации контуры управления
TransientHistoryTime	double	Интервал времени на котором анализируем переходный процесс
TransientObjectIndex	int	Индекс выхода источника сигнала (объекта) по которому анализируем переходный процесс
TransientAverageThreshold	double	Максимально допустимая скорость изменения среднего значения сигнала за интервал времени, по которой принимаем решение о том, что переходный процесс завершен

Переменные состояния класса представлены в таблице (Таблица 3.3).

Таблица 3.3 – Переменные состояния класса NEngineMotionControl

Имя переменной состояния	Тип	Описание
MinAfferentRange	double	Процентная величина от соответствующей разницы *Max-*Min определяющая минимальную ширину диапазона афферетных нейронов изменяяется в интервале [0;1]
CurrentContourAmplitude	std::vector<double>	Текущая амплитуда колебаний
CurrentContourAverage	std::vector<double>	Текущее среднее колебаний
CurrentTransientTime	double	Текущее время переходного процесса
CurrentTransientState	bool	Текущее состояние переходного процесса

В таблице ниже (Таблица 3.4) приведен перечень вариантов реализаций управляющих элементов.

Таблица 3.4 – Список вариантов реализации модели управляющего элемента

Имя прототипа компонента в коллекции	Описание
NMotionElement	СУ двигательной единицей со вставочными интернейронами
NSimpleMotionElement	СУ двигательной единицей без вставочных интернейронов
NBranchedMotionElement	СУ с ветвлением
NSimpleBranchedMotionElement	СУ с ветвлением без вставочных интернейронов
NContinuesBranchedMotionElement	СУ с ветвлением и “непрерывными” нейронами
NContinuesSimpleBranchedMotionElement	СУ с ветвлением и непрерывными нейронами без вставочных интернейронов
NSimplestMotionElement	простейшая СУ
NSimplestBranchedMotionElement	простейшая СУ с ветвлением
NSimplestAfferentBranchedMotionElement	простейшая СУ с ветвлением и простым афферентным нейроном
NNewSimplestAfferentBranchedMotionElement	простейшая СУ с ветвлением, простым афферентным нейроном и обновленной моделью нейрона с выделенным участком мембраны на сому
NAsfNewSimplestAfferentBranchedMotionElement	простейшая СУ с ветвлением, простым афферентным нейроном и обновленной моделью нейрона с выделенным участком мембраны на сому, на 3 афферентных канала
NAslsNewSimplestAfferentBranchedMotionElement	простейшая СУ с ветвлением, простым афферентным нейроном и и обновленной моделью нейрона с выделенным участком мембраны на сому, на 4 афферентных канала

Схема управляющего элемента (Рисунок 2.4) воспроизводится путем выбора режима формирования сети CreationMode=12, и именем управляющего элемента: MotionElementClassName=” NAsfNewSimplestAfferentBranchedMotionElement”.

Все эксперименты проводились при следующих параметрах регулятора:

- AfferentRangeMode=2;

- PacRangeMode=2;

- PacGain=100;

Модель гироскопа

Класс гироскопа, реализующего схему, описанную в п.2.4 реализован в коллекции Libraries/ActLib среды NMSDK. Имя модуля NAstaticGyro. В модуле описан одноименный класс, интерфейс которого описан ниже.

Параметры класса представлены в таблице (Таблица 3.5).

Таблица 3.5 - Параметры класса NAstaticGyro

Имя параметра	Тип	Описание
natural_freq	double	Собственная частота гироскопа
z_g	double	Коэффициент демпфирования гироскопа

Переменные состояния класса представлены в таблице (Таблица 3.6).

Таблица 3.6 - Переменные состояния класса NAstaticGyro

Имя переменной состояния	Тип	Описание
alpha	double	Угол вращения вокруг оси Z
betta	double	Угол вращения вокруг оси X
gamma	double	Угол вращения вокруг оси Y

Все эксперименты проводились при следующих параметрах гироскопа:

- natural_freq = 2000;

- z_g = 0.707.

Модель исследуемой системы

Класс, реализующий систему, описанную в п.2.1 реализован в коллекции Libraries/ActLib среды NMSDK. Имя модуля NManipulatorAndGyro. В модуле описан одноименный класс, интерфейс которого описан ниже.

Параметры класса представлены в таблице ниже (Таблица 3.7).

Таблица 3.7 - Параметры класса NManipulatorAndGyro

Имя параметра	Тип	Описание
Mass	double	Полная масса системы
Length	double	Длина звена манипулятора

Входные данные, используемые классом, представлены в таблице ниже (Таблица 3.8).

Таблица 3.8 - Входные данные класса NManipulatorAndGyro

№ входа	Тип	Описание
	double	Внешний момент, воздействующий на систему
	double	Момент на валу двигателя
	double	текущий угол поворота звена манипулятора по данным датчика манипулятора

Выводы

Были разработаны программные модули расчета модели гироскопа, обновленной модели участков мембраны нейрона, а также программный модуль обеспечения взаимодействия для создания комплексного объекта управления, в составе модуля манипулятора, гироскопа и модели физической среды.

Разработан алгоритм структурной адаптации модели нейронной сети регулятора, обеспечивающий изменение структуры сети для удержания амплитуды колебаний звена манипулятора в заданном диапазоне.

Исследования

План дальнейших исследований

В соответствии с планом исследований, следующими этапами являются:

1. Моделирование системы связанного управления пары звеньев манипулятора (смена и удержание положения).

2. Моделирование системы координированного управления несколькими многозвенниками (поддержание устойчивости).

3. Разработка системы управления движением со множеством многозвенников (шагание).

Выводы

Были проведены исследования обновленной модели нейрона, и показана ее эффективность в задачах, требующих изменения частоты реакций нейрона при постоянном входном воздействии. Типичным случаем, когда такое поведение необходимо, является функционирование нейрона в контуре регуляции, обеспечивающем подавление рассогласования между текущим и ожидаемым положениями, при котором величина рассогласования поступает на вход нейрона. Таким образом, чем дольше рассогласование не компенсируется, тем больше увеличивается активность нейрона, активирующего механизм компенсации.

Эти эффекты были протестированы на модели регулятора, обеспечивающего удержание положения звена манипулятора.

Также было проведено исследование работы контура структурной адаптации регулятора, на примере решения задачи удержания обратного маятника на подвижном основании.

Заключение

1. В работе была выполнена модификация разработанной ранее модели ионного механизма нейрона и улучшены динамические характеристики модели нейрона. Предложено физическое описание объекта управления в среде в целом, и отдельных моделей, в частности модели гироскопа. Также была разработана модель нейросетевого регулятора на импульсных нейронах со структурной адаптацией.

2. Были разработаны программные модули расчета модели гироскопа, обновленной модели участков мембраны нейрона, а также программный модуль обеспечения взаимодействия для создания комплексного объекта управления, в составе модуля манипулятора, гироскопа и модели физической среды. Разработан алгоритм структурной адаптации модели нейронной сети регулятора, обеспечивающий изменение структуры сети для удержания амплитуды колебаний звена манипулятора в заданном диапазоне.

3. Были проведены исследования обновленной модели нейрона, и показана ее эффективность в задачах, требующих из