Шаг 2. Проверка на оптимальность.

На предыдущем этапе найдено допустимое решение. Проверим его на оптимальность Если среди элементов симплексной таблицы, находщихся в строке F (не беря в расчет элемент b₀ - текущее значение целевой функции) нет отрицательных, то найдено оптимальное решение.

Если в строке F есть отрицательные элементы то решение требует улучшения. Выбираем среди отрицательных элементов строки F максимальный по модулю (исключая значение функции b₀)

a_0,l=min{a_0,i }

l - столбец в котором он находится будет ведущим. Для того, что бы найти ведущую строку, находим отношение соответсвующего свободного члена и элемента из ведущего столбца, при условии, что они неотрицательны.

b_k/a_k,l =min {b_i/a_i,l } при a_i,l>0, b_i>0

k - cтрока, для которой это отношение минимально - ведущая. Элемент a_k,l - ведущий (разрешающий). Переменная, соответствующая ведущей строке (x_k) исключается из базиса, переменная соответствующая ведущему столбцу (x_l) включается в базис.

Пересчитываем симплекс-таблицу по формулам. Если в новой таблице после перерасчета в строке F остались отрицательные элементы переходим к шагу 2

Если невозможно найти ведущую строку, так как нет положительных элементов в ведущем столбце, то функция в области допустимых решений задачи не ограничена - алгоритм завершает работу.

Если в строке F и в столбце свободных членов все элементы положительные, то найдено оптимальное решение.

21. Постановка наиболее распространённых задач дискретной оптимизации: задача коммиво-яжера и задача об укладке ранца.

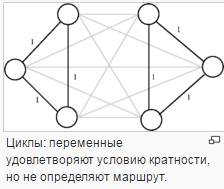
Одним из подходов к решению задачи является формулировка её в виде задачи дискретной оптимизации, при этом решения представляются в виде переменных, а связи — в виде отношений неравенства между ними. Таким образом, возможно несколько вариантов. Например, симметричную задачу можно представить в виде множества ребер V {\displaystyle V}. Каждому ребру {I,j}{\displaystyle \{i,j\}} сопоставляется двоичная переменная 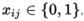{\displaystyle x_{ij}\in \{0,1\}}, равная 1, если ребро принадлежит маршруту, и 0 — в противном случае. Произвольный маршрут можно представить в виде значений множества переменных принадлежности, но не каждое такое множество определяет маршрут. Условием того, что значения множества переменных определяют маршрут, являются описанные далее линейные неравенства.

Каждая вершина должна сообщаться через пару ребер с остальным вершинам, то есть, через входное и выходное ребро:

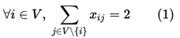
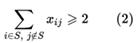
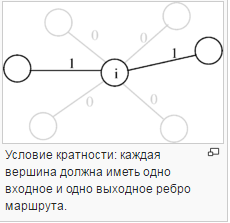
Классическая постановка задачи об укладке ранца:

Пусть имеется набор предметов, каждый из которых имеет два параметра — вес и ценность. Также имеется рюкзак определенной вместимости. Задача заключается в том, чтобы собрать рюкзак с максимальной ценностью предметов внутри, соблюдая при этом весовое ограничение рюкзака.

22. Постановка наиболее распространённых задач дискретной оптимизации: задача о покрытии множества и задача о назначении.

Исходными данными задачи о покрытии множества является конечное множество U {\displaystyle {\mathcal {U}}} и S семейство 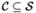{\displaystyle {\mathcal {S}}} его подмножеств. Покрытием называют семейство {\displaystyle {\mathcal {C}}\subseteq {\mathcal {S}}} наименьшей мощности, объединением которых является U{\displaystyle {\mathcal {U}}}. В случае постановки вопроса о разрешении на вход подаётся пара 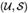{\displaystyle ({\mathcal {U}},{\mathcal {S}})} и целое число k {\displaystyle k}; вопросом является существование покрывающего множества мощности k {\displaystyle k} (или менее).

В качестве примера задачи о покрытии множества можно привести следующую проблему: представим себе, что для выполнения какого-то задания необходим некий набор навыков S {\displaystyle S}. Также есть группа людей, владеющих некоторыми из этих навыков. Необходимо сформировать минимальную группу для выполнения задания, включающую в себя носителей всех необходимых навыков.

Методы решения.

Жадный приближенный алгоритм:

Жадный алгоритм выбирает множества руководствуясь следующим правилом: на каждом этапе выбирается множество, покрывающее максимальное число ещё не покрытых элементов.

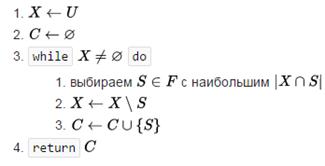
Можно показать, что такой алгоритм показывает время работы (O(H(s) {\displaystyle O(H(s))}, где s {\displaystyle s} — мощность наибольшего множества, и H(n){\displaystyle H(n)}— это сумма первых n{\displaystyle n} членов гармонического ряда.{\displaystyle H(n)=\sum _{k=1}^{n}{\frac {1}{k}}\leq \ln {n}+1}

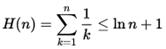
Часто задача о покрытии множества формулируется, как задача целочисленного программирования:

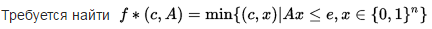
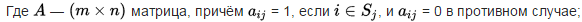
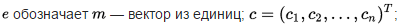
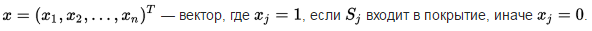
Точное решение может быть получено за полиномиальное время, в случае, когда матрица A{\displaystyle A} вполне унимодулярна.

Сюда можно отнести и задачу о вершинном покрытии на двудольном графе и дереве.

В частности, когда каждый столбец матрицы {\displaystyle A}содержит ровно две единицы, задачу можно рассматривать как задачу рёберного покрытия графа, которая эффективно сводится к поиску максимального паросочетания. На классах задач, где n {\displaystyle n} или m{\displaystyle m} ограничены константой, задача за полиномиальное время решается методами полного перебора.

Задача о назначениях – одна из фундаментальных задач комбинаторной оптимизации в области математической оптимизации или исследовании операций. Задача состоит в поиске минимальной суммы дуг во взвешенном двудольном графе.

В наиболее общей форме задача формулируется следующим образом:

Имеется некоторое число работ и некоторое число исполнителей. Любой исполнитель может быть назначен на выполнение любой (но только одной) работы, но с неодинаковыми затратами. Нужно распределить работы так, чтобы выполнить работы с минимальными затратами.

Если число работ и исполнителей совпадает, то задача называется линейной задачей о назначениях. Обычно, если говорят о задаче о назначениях без дополнительных условий, имеют в виду линейную задачу о назначениях.

23. Область применения и общая идея решения оптимизационных задач методом динамического программирования (ДП). Суть восходящего и нисходящего ДП.

Алгоритм, основанный на МДП (или, короче, ДП-алгоритм), позволяет решить каждую из подзадач один раз и ответ занести в специальную таблицу, для того чтобы в том случае, если на одном из последующих шагов оптимизации эта задача встретится ещё раз, можно было воспользоваться ранее полученным решением.

Динамическое программирование обычно придерживается двух подходов к решению задач:

· нисходящее динамическое программирование: задача разбивается на подзадачи меньшего размера, они решаются и затем комбинируются для решения исходной задачи. Используется запоминание для решений часто встречающихся подзадач.

· восходящее динамическое программирование: все подзадачи, которые впоследствии понадобятся для решения исходной задачи просчитываются заранее и затем используются для построения решения исходной задачи. Этот способ лучше нисходящего программирования в смысле размера необходимого стека и количества вызова функций, но иногда бывает нелегко заранее выяснить, решение каких подзадач нам потребуется в дальнейшем.

24. Последовательность решения задачи определения критических путей сети с помощью метода динамическогопрограммировання.

Наиболее продолжительный полный путь в сетевом графике называется критическим. Критическими также называются работы и события расположенные на этом пути. Работы этого пути определяют общий цикл завершения всего комплекса работ, планируемых при помощи сетевого графика.

Время n(t) завершения последнего n - го узла назовем критическим временем завершения всего комплекса работ. Критическое время обозначим символом Tкр ; Критическим путем назовем путь, который строится обратным ходом, начиная от последнего n - го узла, и достигает первого узла при помощи выделения стрелок, реализующих критическое время; Операции, составляющие критический путь, называются критическими. Замечание. Критический путь может быть неединственным.

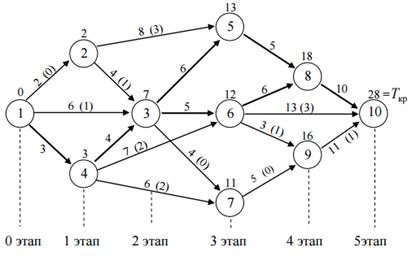
Рисунок 1. Критический путь

Из рисунка 11 вытекает, что сетевой график содержит 5 этапов, T_кр 28 часов. Заметим также, что сетевой график имеет два критических пути, которые на рис. 11 изображены жирными линиями и состоят из следующих узлов:

1 →4 →3 →5 →8 →10 и 1 →4→ 3→ 6→ 8→ 10.

На каждом из критических путей критическое время одно и тоже 28 часов. Свободные резервы времени на некритических операциях с Р_ij на рисунке проставлены в скобках.

25. Последовательность решения задачи коммивояжёра с помощью метода динамическогопрограммировання.

Псевдокод:

Сложность:

26. Представлениезадачи о покрытии множества в видезадачицелочисленногобулевоголинейногопрограммирования.

27. Представлениезадачи о назначении, 0-1-задачи о рюкзаке и задачи коммивояжёра в видезадачицелочисленногобулевоголинейногопрограммирования.

Задача о ранце.
Имеются n предметов, которые необходимо поместить в рюкзак (ранец). Пусть известны вес a_j и «ценность» c_j каждого предмета (j= 1,2,... ,n). Требуется заполнить рюкзак, не превышая его грузоподъемности (объема) b и максимизируя суммарную ценность груза. Получаем следующую булеву ЗЦЛП (задача о рюкзаке):

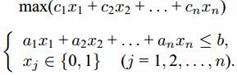
Задача о целочисленном рюкзаке. Предположим теперь, что каждый предмет имеется в неограниченном числе экземпляров, и требуется также максимизировать суммарную ценность груза, не превышая грузоподъемности. Получаем так называемую задачу о целочисленном рюкзаке:

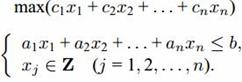
Максимизировать общий вес рюкзака.

Решение. I этап. Условная оптимизация.
f₁(L) = max(2x₁); 0 < x₁ < 1; x₁ = 0,1.
f₁(0) = max[0*2] = 0
f₁(1) = max[0*2, 1*2] = 2
f₁(2) = max[0*2, 1*2] = 2
f₁(3) = max[0*2, 1*2] = 2
f₁(4) = max[0*2, 1*2] = 2
f₁(5) = max[0*2, 1*2] = 2
f₁(6) = max[0*2, 1*2] = 2
f₁(7) = max[0*2, 1*2] = 2
Таблица 1 – Расчет значения функции f₁(L)

f₂(L) = max[3x₂ + f₁(L - 2x₂)]; 0 < x₂ < 3; x₂ = 0,1,2,3.
f₂(0) = max[0*3+0] = 0
f₂(1) = max[0*3+2] = 2
f₂(2) = max[0*3+2, 1*3+0] = 3
f₂(3) = max[0*3+2, 1*3+2] = 5
f₂(4) = max[0*3+2, 1*3+2, 2*3+0] = 6
f₂(5) = max[0*3+2, 1*3+2, 2*3+2] = 8
f₂(6) = max[0*3+2, 1*3+2, 2*3+2, 3*3+0] = 9
f₂(7) = max[0*3+2, 1*3+2, 2*3+2, 3*3+2] = 11
Таблица 2 – Расчет значения функции f₂(L)

f₃(L) = max[2x₃ + f₂(L - 3x₃)]; 0 < x₃ < 3; x₃ = 0,1,2,3.
f₃(0) = max[0*2+0] = 0
f₃(1) = max[0*2+2] = 2
f₃(2) = max[0*2+3] = 3
f₃(3) = max[0*2+5, 1*2+0] = 5
f₃(4) = max[0*2+6, 1*2+2] = 6
f₃(5) = max[0*2+8, 1*2+3] = 8
f₃(6) = max[0*2+9, 1*2+5, 2*2+0] = 9
f₃(7) = max[0*2+11, 1*2+6, 2*2+2] = 11
Таблица 3 – Расчет значения функции f₃(L)

f₄(L) = max[4x₄ + f₃(L - 1x₄)]; 0 < x₄ < 1; x₄ = 0,1.
f₄(0) = max[0*4+0] = 0
f₄(1) = max[0*4+2, 1*4+0] = 4
f₄(2) = max[0*4+3, 1*4+2] = 6
f₄(3) = max[0*4+5, 1*4+3] = 7
f₄(4) = max[0*4+6, 1*4+5] = 9
f₄(5) = max[0*4+8, 1*4+6] = 10
f₄(6) = max[0*4+9, 1*4+8] = 12
f₄(7) = max[0*4+11, 1*4+9] = 13
Таблица 4 – Расчет значения функции f₄(L)

f₅(L) = max[1x₅ + f₄(L - 1x₅)]; 0 < x₅ < 2; x₅ = 0,1,2.
f₅(0) = max[0*1+0] = 0
f₅(1) = max[0*1+4, 1*1+0] = 4
f₅(2) = max[0*1+6, 1*1+4, 2*1+0] = 6
f₅(3) = max[0*1+7, 1*1+6, 2*1+4] = 7
f₅(4) = max[0*1+9, 1*1+7, 2*1+6] = 9
f₅(5) = max[0*1+10, 1*1+9, 2*1+7] = 10
f₅(6) = max[0*1+12, 1*1+10, 2*1+9] = 12
f₅(7) = max[0*1+13, 1*1+12, 2*1+10] = 13
Таблица 5 – Расчет значения функции f₅(L)

II этап. Безусловная оптимизация.
Таким образом, максимальный вес рюкзака f₅(7) равна 13 кг.
При этом x₅ = 0, так как f₅(7) = 13 достигается при х₅=0 (см. таблицу 5).
Предметы остальных типов распределяются следующим образом:
L = 7 - 1 * 0 = 7
f₄(7) = 13 достигается при х₄ = 1 (см. таблицу 4).
L = 7 - 1 * 1 = 6
f₃(6) = 9 достигается при х₃ = 0 (см. таблицу 3).
L = 6 - 3 * 0 = 6
f₂(6) = 9 достигается при х₂ = 3 (см. таблицу 2).
L = 6 - 2 * 3 = 0
f₁(0) = 0 достигается при х₁ = 0 (см. таблицу 1).
L = 0 - 1 * 0 = 0
В итоге наилучший вариант загрузки рюкзака достигается при значениях: x₁ = 0, x₂ = 3, x₃ = 0, x₄ = 1, x₅ = 0

28. Обобщённая схема классического генетического алгоритма. Краткая характеристика основных операторов генетического алгоритма (операторы репродукции, кроссинговера, мутации).

Основные операторы ГА

Оператор репродукции (селекции) – искуственная версия естественного отбора, основанного на принципе выживания более приспособленных особей. В результате выполнения этого оператора хромосомы копируются в промежуточную популяцию для дальнейшего «размножения» согласно их значениям фитнесс-функции.

Оператор кроссинговера (скрещивания)­ – основан на принципе наследования потомками генетической информации родителей и определяет передачу признаков (наследственной информации) родителей потомкам.

Оператор мутации – основан на принципе резкого изменения свойств потомков и приобретении у них свойств, отсутствующих у родителей; позволяет повысить разнообразие (изменчивость) особей в популяции (множество решений).

Рисунок 1 – Блок-схема классического (простого) ГА

ПРАКТИКА:

1. Используя программную среду MATLAB, произвестилокальнуюлинейную интерполяцию, а такжеинтерполяцию на основе кубического сплайнафункциональнойзвисимостиy = f(x), представленной рядом значенийxиy:

X -3,5 -2,4 -1,8 0,14 2,12 3,64 5,29 7,72

Y 1,2 2,5 7,3 11,6 12,8 14,9 20,1 24,0.