Алгоритм поиска допустимого решения ЗЛП на основе симплекс-таблиц.

проверка допустимости решения ЗЛП на основе заполненной симплекс-таблицы. В качестве признака допустимости решения ЗЛП выступает требование неотрицательности всех элементов второго столбца (коэффициентов 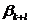) симплекс-таблицы (коэффициент 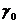в расчёт не принимается).

Если данное требование не выполняется (т.е. среди коэффициентов 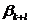имеется хотя бы один отрицательный), то осуществляется замена базисных переменных на свободные в соответствии с алгоритмом, описанным в приложении 4 лабораторной работы №5. При этом если в ходе поиска допустимого решения возникнет ситуация, когда в симплекс-таблице один или несколько элементов второго столбца отрицательны, и хотя бы в одной строке, соответствующей одному из этих элементов, остальные элементы положительны, то это свидетельствует об отсутствии у ЗЛП допустимого решения.

Алгоритм поиска оптимального решения ЗЛП на основе симплекс-таблиц.

проверка данного допустимого решения на оптимальность. Признаком оптимальности решения ЗЛП является требование отрицательности всех элементов второй строки (коэффициентов r_j) симплекс-таблицы (коэффициент 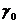в расчёт не принимается). Если данное требование не выполняется (т.е. среди коэффициентов r_j имеется хотя бы один положительный), то осуществляется замена базисных переменных на свободные в соответствии с алгоритмом, описанным в приложении 3 лабораторной работы №5, до тех пор, пока не будет получено единственное оптимальное решение. При этом искомыми оптимальными значениями переменных будут значения базисных переменных второго столбца конечной симплекс-таблицы, а минимальным значением целевой функции – значение 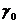. В принципе, можно решать задачу получения оптимального решения и добиваясь положительности всех элементов второй строки, но в таком случае минимальным значением целевой функции будет значение 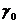, взятое с отрицательным знаком.

При этом если в ходе поиска оптимального решения возникнет ситуация, когда во второй строке симплекс-таблицы один или несколько элементов равны нулю (коэффициенты r_j), а все остальные отрицательны, то это свидетельствует о том, что данная ЗЛП имеет бесчисленное множество оптимальных решений.

Например, если коэффициент r₂ = 0, то имеет место выражение для целевой функции 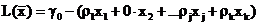, где переменная x₂, а, следовательно, и сама целевая функция могут принимать произвольное значение.

Если же в ходе поиска оптимального решения окажется, что во второй строке симплекс-таблицы один или несколько элементов положительны, а в столбце, соответствующем положительному элементу, остальные элементы (коэффициенты 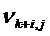) отрицательны, то это свидетельствует о том, что данная ЗЛП не имеетоптимального решения.

20. Алгоритм поиска оптимального решения ЗЛП на основе симплекс-таблиц.

Табличный симплекс-метод

Для упрощения процесса решения исходные данные задачи линейного программирования при решении ее симплекс методом записываются в специальные симплекс-таблицы. Поэтому одна из модификаций симплекс метода получила название табличный симплекс метод. Задача линейного программирования в каноническом виде:

F=a_0,1x₁+a_0,2x₂+...a_0,nx_n +b₀ → max

a_1,1x₁+a_1,2x₂+...a_1,nx_n + x_n+1=b₁

a_2,1x₁+a_2,2x₂+...a_2,nx_n +x_n+2 =b₂

.......................................

a_m,1x₁+a_m,2x₂+...a_m,nx_n+x_n+m=b_m

Исходная таблица для задачи имеет следующий вид:

	x1	x2	...	xn-1	xn	b
F	-a0,1	-a0,2	...	-a0,n-1	-a0,n	-b0
xn+1	a1,1	a1,2	...	a1,n-1	a1,n	b1
xn+2	a2,1	a2,2	...	a2,n-1	a2,n	b2
...	...	...	...	...	...	...
xn+m	am,1	am,2	...	am,n-1	am,n	bm

x₁, x₂, x_n - исходные переменные, x_n+1, x_n+2, x_n+m - дополнительные переменные. Все дополнительные переменные мы приняли как базисные, а исходные переменные как небазисные(дополнительные записаны в первый столбец симплекс-таблицы а исходные в первую строку). При каждой итерации элементы симплекс-таблицы пересчитывают по определеннымправилам.

Алгоритм симплекс-метода.

Подготовительный этап

Приводим задачу ЛП к каноническому виду

F=a_0,1x₁+a_0,2x₂+...a_0,nx_n +b₀ → max

a_1,1x₁+a_1,2x₂+...a_1,nx_n+x_n+1=b₁

a_2,1x₁+a_2,2x₂+...a_2,nx_n+x_n+2=b₂

.......................................

a_m,1x₁+a_m,2x₂+...a_m,nx_n+x_n+m=b_m

В случае если в исходной задаче необходимо найти минимум - знаки коэффициентов целевой функции F меняются на противоположные a_0,n=-a_0,n. Знаки коэффициентов ограничивающих условий со знаком "≥" так же меняются на противоположные. В случае если условие содержит знак "≤" - коэффициенты запишутся без изменений.