Постановка задачи линейного программирования. Основная задача линейного программирования (ЗЛП) и условия наличия у неё допустимого решения.

Задача линейной оптимизации характеризуется тем, что целевая функция L( 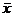) и ограничения в виде равенств и/или неравенств 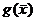( 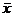= (x₁,…,x_n) – вектор переменных) – линейные. При этом в своей исходной постановке задача линейной оптимизации может характеризоваться тем, что требуется отыскать либо минимум, либо максимум целевой функции, а в качестве ограничений могут выступать линейные равенства и неравенства одновременно.

Hайти такие неотрицательные значения переменных x₁, x₂, …,x_n, которые удовлетворяют ограничениям

a₁₁x₁ + a₁₂x₂ + … + a_1jx_j +… + a_1nx_n = b₁;

a₂₁x₁ + a₂₂x₂ + … + a_2jx_j + … + a_2nx_n = b₂;

…………………………………………

a_j1x₁ + a_j2x₂ + … + a_ijx_j + … + a_inx_n = b_i;

…. ……………………………………. (1)

a_m1x₁ + a_m2x₂ + … + a_mjx_j + … + a_mnx_n = b_m

и обращают в минимум целевую функцию

L( 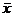) = c₁x₁ + c₂x₂ + … + c_jx_j + … + c_nx_n. (2)

При этом коэффициенты a_ijв системе ограничений и коэффициенты c_jцелевой функции могут принимать как положительные, так и отрицательные значения.

В такой постановке задача линейной оптимизации называется основной задачей линейного программирования (ОЗЛП).

Совокупность неотрицательных значений переменных x₁, x₂, …, x_n, удовлетворяющих ограничениям (2), называется допустимым решением ОЗЛП, а совокупность всех допустимых решений представляет собой подмножество допустимых решений ОЗЛП. Допустимое решение ОЗЛП в виде совокупности значений 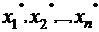переменных, обеспечивающих минимальное значение целевой функции L( 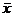), называется оптимальным решением ОЗЛП.

Переход от задачи линейного программирования (ЗЛП) с ограничениями-неравенствами к канонической и стандартной формам представления ЗЛП.

– Если в исходной постановке задачи оптимизации присутствуют ограничения-неравенства, то переход от ограничений-неравенств к ограничениям-уравнениям можно осуществить по следующим правилам.

Так, если в системе ограничений присутствует неравенство, у которого левая часть меньше правой, т.е. неравенство вида

a_i1x₁ + a_i2x₂ + … + a_ijx_j +… + a_inx_n ≤ b_i,

то к его левой части необходимо прибавить неотрицательную величину x_n+i. В таком случае данное неравенство преобразуется в уравнение

a_i1x₁ + a_i2x₂ + … + a_ijx_j +… + a_inx_n + x_n+i= b_i.

Аналогично, если в системе ограничений присутствует неравенство, у которого левая часть больше правой, т.е. неравенство вида

a_i1x₁ + a_i2x₂ + … + a_ijx_j +… + a_inx_n ≥ b_i,

то из его левой части необходимо вычесть неотрицательную величину x_n+i . В таком случае данное неравенство преобразуется в уравнение

a_i1x₁ + a_i2x₂ + … + a_ijx_j +… + a_inx_n – x_n+i=b_i.

– Для этого, во-первых, в системе уравнений-ограничений (1) базисные переменные выражаются через свободные. В результате получается система уравнений вида

;

;

............................................................................

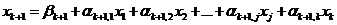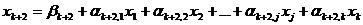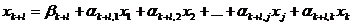; (3)

……………………………………………… ,

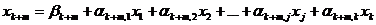где коэффициенты 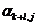являются комбинациями коэффициентов a_ijиb_i.

Целевая функция вида (2) также выражается через свободные переменные и в результате принимает вид

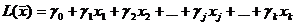, (4)

где коэффициенты 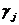являются комбинациями коэффициентов c_j.

Затем система уравнений (3) и выражение для целевой функции (4) преобразуются к виду

;

…………………………………………………

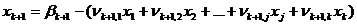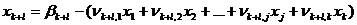; (5)

…………………………………………………

,

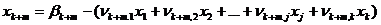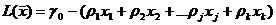, (6)

где 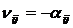; .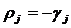