Последовательность решения задачи безусловнойнелинейнойоптимизацииметодом наискорейшего спуска.

Метод наискорейшего спуска относится к поисковым градиентным методам решения задач нелинейной оптимизации, т.е. использующим вычисление целевой функциипроизводной, и позволяющим получить приближенное решение с некоторой заданной точностью. Достоинством данного метода является то, что среди других поисковых методов он обеспечивает наименьшее число шагов решения задачи поиска.

В основе градиентных методов решения задач нелинейной оптимизации лежит следующая идея.

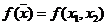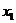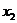Рассмотрим функцию двух переменных и . Проекция линии пересечения функции 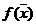с плоскостью 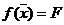(F – некоторое заданное значение функции 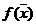) на плоскости 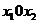называется линией постоянного уровня. Задавая различные значения 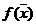, можно получить другие линии постоянного уровня и представить функцию 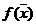совокупностью этих линий. Перемещение по поверхности, отображающей функцию 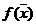, из точки 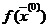в точку 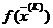, эквивалентно перемещению из точки 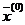в точку 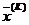на плоскости 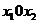. Если это перемещение осуществлять в направлении убывания функции 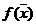, то через определённое число шагов (итераций) можно достигнуть окрестности точки локального минимума.

Идея метода наискорейшего спуска состоит в следующем.

Есл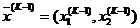и и 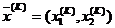– начальная и конечная точки перемещения (поиска) на k-ом шаге, то они связаны соотношением

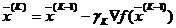, (1)

где – 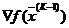–вектор антиградиента, задающий направление наибольшего убывания функции, а 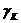– величина шага перемещения.

Учитывая, что вектор градиента функции в данной точке есть набор значений её частных производных в этой точке, т.е. в случае двух переменных

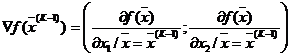, (2)

получим следующее выражение для определения координат конечной точки перемещения на k-ом шаге:

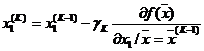, (3)

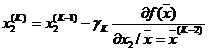, (4)

где правые сомножители второго слагаемого правой части означают, что частные производные функции 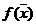вычисляются в точке .

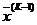Если из точки 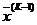поиск ведётся в направлении антиградиента

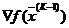– , то в точке 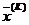, являющейся начальной точкой следующего шага, направление поиска будет определяться антиградиентом– 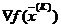. Векторы 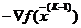и 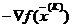в точке 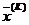перпендикулярны, откуда следует, что их скалярное произведение в данной точке равно 0, т.е.

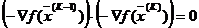
(5)

или .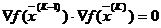

С учётом (2) выражение (5) примет вид:

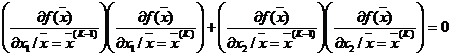. (6)

Решение уравнения (6) совместно с (3),(4) позволяет определить величину 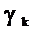на k-ом шаге поиска по методу наискорейшего спуска. Процесс поиска минимума в соответствии с (3) и (4) будет продолжаться до тех пор, пока не будет выполнено условие:

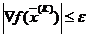, (7)

где 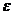– требуемая точность определения минимума функции 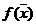. Величина 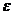задаёт размеры окрестности точки минимума, удовлетворяющие заданной точности. С учётом (2) выражение (7) примет вид:

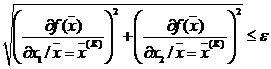. (8)

Таким образом, выражения (3), (4), (6), (8) являются основными рабочими соотношениями решения задач нелинейной оптимизации методом наискорейшего спуска.

Следует отметить, что в принципе процесс поиска по методу наискорейшего спуска может закончиться в стационарной точке (т.е. такой точке, в которой частные производные целевой функции по каждой координате равны нулю) любого типа: или действительно в точке локального экстремума или в седловой точке. Тип стационарной точки можно установить, проверив условие положительной определённости матрицы Гессе (матрицы вторых частных производных целевой функции в данной точке), а именно: все главные миноры матрицы Гессе должны быть неотрицательными. Если это условие не выполняется, то данная стационарная точка является седловой. В таком случае необходимо выйти из неё, используя какой-либо неградиентный метод, а затем продолжить процедуру наискорейшего спуска.

Пример.Отыскатьминимумфункцииf(x) = x₁² + 2x₂² – 2x₁ – 8x₂ + 12 с точностью e = 0,6 при начальном значении x⁰ = (6;8).

Найдем в первую очередь частные производные целевой функции :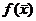

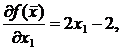
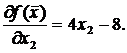
В соответствии с формулами (2), (3) координаты точки на k-ом шаге поиска рассчитываются следующим образом:

x₁^(k) = x₁^(k-1) – g_k(2 x₁^(k-1)–2), (9)
x₂^(k) = x₂^(k-1) –g_k(4 x₂^(k-1)–8). (10)

Для определения величины шага g_k используем уравнение (6), которое в данном случае имеет вид:

(2x₁^(k-1) – 2)(2x₁^(k) – 2) + (4x₂^(k-1) – 8)(4x₂^(k) – 8) = 0. (11)

Поисковая процедура завершается при выполнении условия (8)

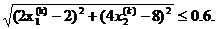(12)

Последовательность поиска оптимального решения в соответствии (9)–(12) следующая.

Поскольку начальной точкой поиска является 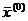= (6;8), то координаты точки в конце 1-го шага (k=1) определяются в соответствии с (9)–(12) следующими образом:

x₁⁽¹⁾ = x₁⁽⁰⁾ –g₁(2 x₁⁽⁰⁾ – 2),
x₂⁽¹⁾ = x₂⁽⁰⁾ –g₁(4 x₂⁽⁰⁾ – 8).

Тогда

x₁⁽¹⁾ = 6 –g₁(2×6 – 2) = 6 –g₁10,
x₂⁽¹⁾ = 8 –g₁(4×8 – 8) = 8 –g₁24.

Подставляя значения x₁⁽⁰⁾ = 6, x₂⁽⁰⁾ = 8, а также только что определенные значения x₁⁽¹⁾ и x₂⁽¹⁾ в (11), получим:

(2×6–2)(2×(6–10g₁)–2) + (4×8 – 8)(4× (8 – 24g₁) – 8) = 0,
10(10 – 20g₁) + 24(24 – 96g₁) = 0,
100 – 200g₁ + 576 – 2304g₁ = 0,
–2504g₁ = –676.

Тогда g₁ = 0.27.

Определим, используя найденное значение g₁, координаты точки на 1-ом шаге:

x₁⁽¹⁾ = 6 – 0.26×10 = 3.3,
x₂⁽¹⁾ = 8 – 0.26×24 = 1.52.

Проверим выполнение условия (12):

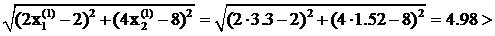e.

Поскольку условие (12) не выполняется, перейдем ко 2-му шагу (k=2), исходной точкой которого будет 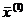= (3.3;1.52). В соответствии с (9),(10) можно записать:

x₁⁽²⁾ = x₁⁽¹⁾–g₂(2 x₁⁽¹⁾–2)= 3.3 –g₂(2×3.3 – 2) = 3.3 –g₂4.6;
x₂⁽²⁾ = x₂⁽¹⁾–g₂(4 x₂⁽¹⁾–8) =1.52 –g₂(4×1.52 – 8) = 1.52 + g₂1.92.

Подставляя значения x₁⁽¹⁾ = 3.30, x₂⁽¹⁾ = 1.52, а также только что определенные значения x₁⁽²⁾ и x₂⁽²⁾ в (11), получим:

(2×3.3 – 2)(2× (3.3 – 4.6g₂) – 2) + (4×1.52 – 8)(4× (1.52 + 1.92g₂) – 8) =

= 4.6(4.6 – 9.2g₂) + (–1.92)(–1.92 + 7.68g₂) = 0,

откуда g₂ = 0.436. Определим, используя найденное значение g₂, координаты точки на 2-ом шаге согласно (9),(10):

x₁⁽²⁾ = 3.30 – 0.436×4.6 = 1.29,
x₂⁽²⁾ = 1.52 + 0.436×1.92 = 2.36.

Проверим выполнение условия (12):

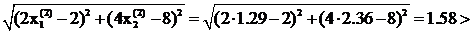e.

Поскольку условие (12) не выполняется, перейдем к 3-му шагу (k=3), исходной точкой которого будет 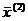= (1.29;2.36). В соответствии с (9),(10) можно записать:

x₁⁽³⁾ = x₁⁽²⁾ –g₃(2 x₁⁽²⁾–2) = 1.29 –g₃(2×1.29 – 2) = 1.29 –g₃0.58,
x₂⁽³⁾ = x₂^{(2 )} –g₃(4 x₂⁽²⁾–8) = 2.36 –g₃(4×2.36 – 8) = 2.36 –g₃1.44.

Уравнение (11) для определения g₃ примет вид

(2×1.29 – 2)(2×(1.29 – 0.58g₃) – 2) + (4×2.36 – 8)(4×(2.36 – 1.44g₃)–8) =

= 0.58(0.58 – 1.16g₃) + 1.44(1.44 – 5.76g₃) = 0,

откуда g₃ = 0.28.

Тогда координаты точки в конце третьего шага будут иметь значения:

x₁⁽³⁾ = 1.29 – 0.28×0.58 = 1.13,
x₂⁽³⁾ = 2.35 – 0.28×1.44 = 1.96.

Проверим выполнение условия (12):

.

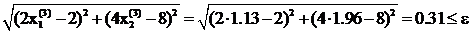Таким образом, на третьем шаге оптимизацииобеспечивается заданная точность, а полученной стационарной точкой будет 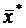= (1.13;1.96).

Установим характер этой стационарной точки посредством проверки условия положительной определённости матрицы Гессе (матрицы вторых частных производных целевой функции в данной точке).

Итак, вторая частная производная по координате x₁равна 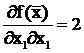, вторая частная производная по координате x₂ равна 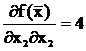, а смешанные производные по координатам x₁и x₂ равны 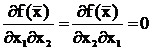. Таким образом, матрица Гессе имеет вид 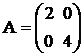.Её главные миноры первого и второго порядка соответственно равны 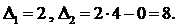Следовательно, поскольку матрица Гессе является положительно определённой, в точке 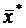= (1.13;1.96) находится локальный минимум целевой функции, а минимальнымзначеним целевойфункциибудет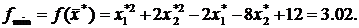

Для удобства проведения расчетов в процессе поиска минимума целевой функции методом наискорейшего спуска целесообразно пользоваться таблицей вида:

k
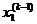		3.3	1.29
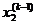		1.52	2.36
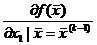		4.6	0.58
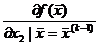		–1.92	1.44
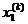	6–10g1	3.3	3.3–4.6g2	1.29	1.29–0.58g3	1.13
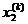	8–24g1	1.52	1.52+1.92g2	2.36	2.36–1.44g3	1.96
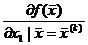	10–20g1	4.6	4.6–9.2g2	0.58	0.58–1.16g3	0.26
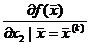	24 – 96g1	–1.92	–1.92+7.68g2	1.44	1.44–5.76g3	–0.17
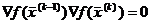	676–23504g1=0	24.85–57.07g2=0	2.41–8.96g3=0
gk	0.27	0.436	0.28
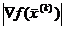	4.98	1.58	0.31