Постановка задачиквадратическогопрограммирования и способеёрешения с помощьюпрограммнойсреды МАТLAB.

Квадратичное программирование – область математического программирования, посвященная теории решения задач, характеризующихся квадратичной зависимостью между переменными.

Программирование в управлении можно представить как процесс распределения ресурсов. Существует ряд различных методов, основанных на идеях математического программирования, среди которых широкое применение нашел метод квадратичного программирования.

Применение метода квадратичного программирования актуально в сегодняшнее время, так как использование математических моделей является важным направлением совершенствования планирования и анализа деятельности компании. Представление данных в виде математической модели позволяет конкретизировать информацию, создавать и моделировать варианты, выбирать оптимальные решения.

1. Постановка задачи квадратичного программирования

Пусть задана квадратичная функция

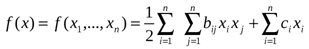(1*)

или в векторно-матричной форме

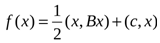(1)

и линейные неравенства

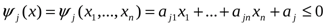
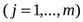, (2*)

которые в векторно-матричной форме запишем так:

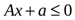, (2)

и пусть неравенства (2) определяют некоторую область Ω, содержащую внутренние точки.

Будем предполагать, что матрица 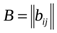симметричная и положительно определенная, так что 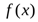- выпуклая функция.

Задача квадратичного программирования формулируется так: отыскать точку 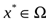, для которой достигается минимум функции (1) при ограничениях (2):

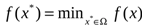(3)

При этом задача квадратичного программирования является просто задачей нелинейного программирования с квадратичной целевой функцией и линейными ограничениями. И может формулироваться следующим образом: найти

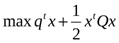при ,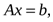

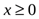где -мерный вектор, - симметричная матрица 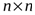, 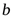- -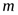мерный вектор и 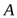- матрица .

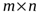Из всех задач нелинейного программирования задача квадратичного программирования является самой легкой для решения и лишь немного сложнее, чем задача линейного программирования. Рассмотрим на примере.

Пример:Финансист обдумывает, как распределить свои фонды между возможными инвестициями. Предположим, что инвестиция 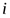имеет ожидаемую прибыль 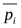на каждый вложенный доллар. Тогда, если 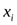- количество вклада в 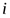-ю инвестицию, то ожидаемая прибыль выражается, как .

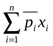В среде MATLAB задачи квадратичного программирования решаются с помощью функции quadprog. Доклад посвящён краткому описанию её воз-можностей. 1 ◦ . Функция quadprog решает задачу квадратичного программирования в форме 1 2 x T · H · x + f T · x → inf, A · x 6 b, Aeq · x = beq, lb 6 x 6 ub. (1) Основными входными параметрами quadprog являются: матрица H и век- тор f из целевой функции, матрица ограничений-неравенств A, вектор пра- вых частей ограничений-неравенств b, матрица ограничений-равенств Aeq, вектор правых частей ограничений-равенств beq, вектор lb, ограничивающий план x снизу, вектор ub, ограничивающий план x сверху. На выходе функция quadprog выдаёт оптимальный план x задачи (1) и экстремальное значение целевой функции fval.