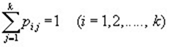Уравнения линейной регрессии У на Х и Х на У. Коэффициент регрессии.

В теории вероятностей под термином «регрессия» и понимают эту функцию, которая есть не что иное как условное математическое ожидание случайной переменной Y при условии, что другая случайная переменная X приняла значение x. Если, например, пара (X, Y) имеет двумерное нормальное распределение с E(X)=μ₁, E(Y)=μ₂, var(X)=σ₁², var(Y)=σ₂², cor(X, Y)=ρ, то можно показать, что условное распределение Y при X=x также будет нормальным с математическим ожиданием, равным

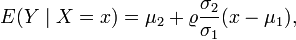
и дисперсией

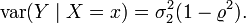
В этом примере регрессия Y на X является линейной функцией. Если регрессия Y на X отлична от линейной, то приведённые уравнения суть линейная аппроксимация истинного уравнения регрессии.

В общем случае регрессия одной случайной переменной на другую не обязательно будет линейной. Также не обязательно ограничиваться парой случайных переменных. Статистические проблемы регрессии связаны с определением общего вида уравнения регрессии, построением оценок неизвестных параметров, входящих в уравнение регрессии, и проверкой статистических гипотез о регрессии^[2]. Эти проблемы рассматриваются в рамках регрессионного анализа.

КОЭФФИЦИЕНТ РЕГРЕССИИ - Одна из характеристик связи между зависимой у и независимой переменной х. К. р. показывает, на сколько единиц увеличивается значение, принимаемое у, если переменная х изменится на единицу своего изменения. Геометрически К. р. является угловым коэффициентом наклона прямой линии у.

Цепи Маркова. Матрица переходных вероятностей.

Це́пьМа́ркова — последовательность случайных событий с конечным или счётным числом исходов, характеризующаяся тем свойством, что, говоря нестрого, при фиксированном настоящем будущее независимо от прошлого. Названа в честь А. А. Маркова (старшего).

Определение

Последовательность дискретных случайных величин 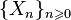называется простой цепью Маркова (с дискретным временем), если

.

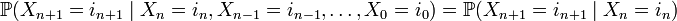Таким образом, в простейшем случае условное распределение последующего состояния цепи Маркова зависит только от текущего состояния и не зависит от всех предыдущих состояний (в отличие от цепей Маркова высших порядков).

Область значений случайных величин 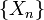называется простра́нствомсостоя́ний цепи, а номер 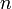— номером шага.

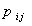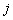Переходной вероятностью называют условную вероятность того, что из состояния в итоге следующего испытания система перейдет в состояние . Таким образом, индекс относится к предшествующему, а 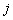– к последующему состоянию.

Будем считать, что число состояний конечно и равно k.

Матрицей перехода системы называют матрицу, которая содержит все переходные вероятности этой системы:

,

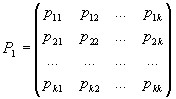где 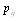представляют вероятности перехода за один шаг.

Отметим некоторые особенности матрицы перехода:

Элементы каждой строки матрицы представляют собой вероятности всех возможных переходов за один шаг из выбранного состояния, в том числе и вероятность отсутствия перехода (элемент строки с равными индексами); Элементы столбцов задают вероятности всех переходов системы за один шаг в заданное состояние.

Так как в каждой строке матрицы помещены вероятности событий (т.е. вероятности перехода из состояния в любое возможное состояние 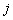), которые образуют полную группу, то сумма вероятностей этих событий равна единице:

По главной диагонали матрицы перехода стоят вероятности 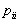того, что система не выйдет из состояния, а останется в нем.