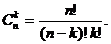Элементы комбинаторного анализа.

Элементы комбинаторного анализа.

Основные правила комбинаторики. Правило умножения (основная теорема комбинаторики).Общее число N способов, которыми можно получить упорядоченную совокупность (a₁,a₂,...a_k), где a_iÎA_i (т.е. выбрать по одному элементу из каждой группы и расставить их в определенном порядке), равно

.

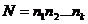Б. Правило сложения. Если один элемент из группы A_i можно выбрать n_i способами, и при этом любые две группы A_i и A_j не имеют обших элементов, то выбор одного элемента или из A₁, или из A₂, ..., или из A_k можно осуществить

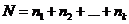способами.

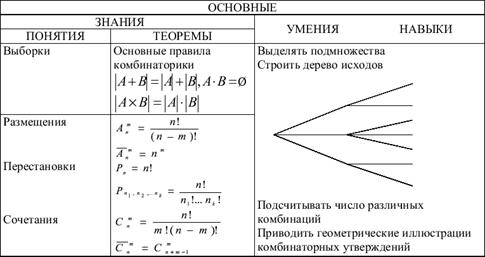
размещения– это упорядоченные совокупности k элементов из n, отличающиеся друг от друга либо составом, либо порядком элементов.

Например. Пусть имеется множество 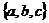из трех элементов. Тогда все размещения двух элементов из трех таковы: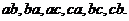

Перестановки – это упорядоченные совокупности, отличающиеся друг от друга только порядком элементов.

Число всех перестановок множества из n элементов обозначается 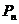и вычисляется по формуле

.

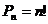сочетания– это неупорядоченные совокупности элементов, отличающиеся друг от друга только составом элементов.

Например.Все сочетания без повторений двух элементов из множества :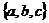

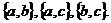
Формула для вычисления числа сочетаний n элементов по k:

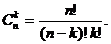
Основные понятия теории вероятностей.

• Событием называется любой исход опыта, различают следующие виды событий:

- случайные

- достоверные

- невозможные

Понятие достоверного и невозможного события используется для

количественной оценки возможности появления того или иного явления, а с

количественной оценкой связана вероятность.

• Вероятность — численная мера возможности наступления некоторого события.

• Вероятностное пространство

• Случайная величина — это величина, которая принимает в результате опыта одно из множества значений, причём появление того или иного значения этой величины до её измерения нельзя точно предсказать.

Вероятностное пространство.

Вероя́тностноепростра́нство — понятие, введённое А. Н. Колмогоровым в 30-х годах XX века для формализации понятия вероятности, которое дало начало бурному развитию теории вероятностей как строгой математической дисциплины.

Вероятностное пространство — это тройка 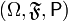(иногда обрамляемая угловыми скобками: 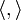), где

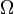§ — это произвольное множество, элементы которого называются элементарными событиями, исходами или точками;

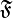§ — сигма-алгебра подмножеств 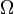, называемых (случайными) событиями;

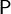§ — вероятностная мера или вероятность, т.е. сигма-аддитивная конечная мера, такая что .

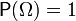Замечания

§ Элементарные события (элементы 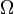), по определению, — это исходы случайного эксперимента, из которых в эксперименте происходит ровно один.

§ Каждое случайное событие (элемент 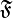) — это подмножество 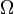. Говорят, что в результате эксперимента произошло случайное событие 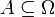, если (элементарный) исход эксперимента является элементом .
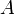Требование, что 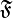является сигма-алгеброй подмножеств 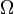, позволяет, в частности, говорить о вероятности случайного события, являющегося объединением счетного числа случайных событий, а также о вероятности дополнения любого события.

Простым и часто используемым примером вероятностного пространства является конечное пространство. Пусть 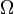— конечное множество, содержащее 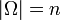элементов.

В качестве сигма-алгебры удобно взять семейство подмножеств 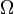. Его часто символически обозначают 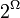. Легко показать, что общее число членов этого семейства, т.е. число различных случайных событий, как раз равно 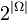, что объясняет обозначение.

Вероятность, вообще говоря, можно определять произвольно. Часто, однако, нет причин считать, что один элементарный исход чем-либо предпочтительнее другого. Тогда естественным способом ввести вероятность является:

,

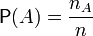где 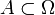, и 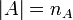- число элементарных исходов, принадлежащих .

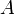В частности, вероятность любого элементарного события:

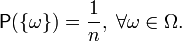
Формула полной вероятности.

Формула полной вероятности позволяет вычислить вероятность интересующего события через условные вероятности этого события в предположении неких гипотез, а также вероятностей этих гипотез.

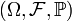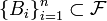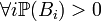
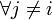
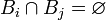
Пусть дано вероятностное пространство , и полная группа попарно несовместных событий , таких что 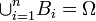. Пусть 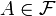— интересующее нас событие. Тогда

.

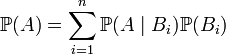Формула полной вероятности также имеет следующую интерпретацию. Пусть 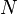— случайная величина, имеющая распределение

.

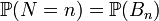Тогда

,

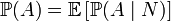т.е. априорная вероятность события равна среднему его апостериорной вероятности.

Теорема Байеса.

Теорема Байеса (или формула Байеса) — одна из основных теорем теории вероятностей, которая позволяет определить вероятность того, что произошло какое-либо событие (гипотеза) при наличии лишь косвенных тому подтверждений (данных), которые могут быть неточны. Названа в честь её автора, преп. Томаса Байеса (посвящённая ей работа «AnEssaytowardssolving a ProblemintheDoctrineofChances» впервые опубликована в 1763 году,[1] через 2 года после смерти автора). Полученную по формуле вероятность можно далее уточнять, принимая во внимание данные новых наблюдений.

Психологические эксперименты[2] показали, что люди при оценках вероятности игнорируют различие априорных вероятностей (ошибка обоснования оценки (англ.)русск.), и потому результаты по формуле Байеса и правильные результаты могут сильно отличаться от ожидаемых.

Формула Байеса:

,

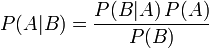где

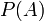— априорная вероятность гипотезы A (смысл такой терминологии см. ниже);

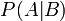— вероятность гипотезы A при наступлении события B (апостериорная вероятность);

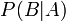— вероятность наступления события B при истинности гипотезы A;

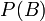— полная вероятность наступления события B.

Формула Бернулли.

Формула Бернулли — формула в теории вероятностей, позволяющая находить вероятность появления события A при независимых испытаниях. Формула Бернулли позволяет избавиться от большого числа вычислений — сложения и умножения вероятностей — при достаточно большом количестве испытаний. Названа в честь выдающегося швейцарского математика Якоба Бернулли, выведшего формулу.

Теорема: Если Вероятность p наступления события Α в каждом испытании постоянна, то вероятность 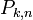того, что событие A наступит k раз в n независимых испытаниях, равна: 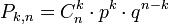, где .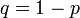

Локальная теорема Лапласа.4

Теорема Муавра — Лапласа — одна из предельных теорем теории вероятностей, установлена Лапласом в 1812 году. Если при каждом из n независимых испытаний вероятность появления некоторого случайного события Е равна р (0<р<1) и m — число испытаний, в которых Е фактически наступает, то вероятность неравенства близка (при больших n) к значению интеграла Лапласа.

Если в схеме Бернулли n стремится к бесконечности, p (0 < p < 1) постоянно, величина 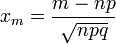ограничена равномерно по m и n 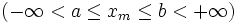, то

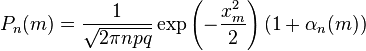
где 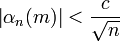, c > 0, c — постоянная.

Приближённую формулу

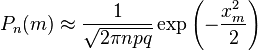
рекомендуется применять при n > 100 и npq> 20.

Определение

Последовательность дискретных случайных величин 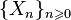называется простой цепью Маркова (с дискретным временем), если

.

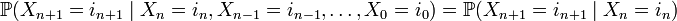Таким образом, в простейшем случае условное распределение последующего состояния цепи Маркова зависит только от текущего состояния и не зависит от всех предыдущих состояний (в отличие от цепей Маркова высших порядков).

Область значений случайных величин 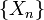называется простра́нствомсостоя́ний цепи, а номер 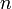— номером шага.

Переходной вероятностью 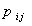называют условную вероятность того, что из состояния в итоге следующего испытания система перейдет в состояние 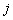. Таким образом, индекс относится к предшествующему, а 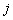– к последующему состоянию.

Будем считать, что число состояний конечно и равно k.

Матрицей перехода системы называют матрицу, которая содержит все переходные вероятности этой системы:

,

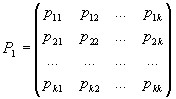где 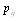представляют вероятности перехода за один шаг.

Отметим некоторые особенности матрицы перехода:

Элементы каждой строки матрицы представляют собой вероятности всех возможных переходов за один шаг из выбранного состояния, в том числе и вероятность отсутствия перехода (элемент строки с равными индексами); Элементы столбцов задают вероятности всех переходов системы за один шаг в заданное состояние.

Так как в каждой строке матрицы помещены вероятности событий (т.е. вероятности перехода из состояния в любое возможное состояние 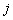), которые образуют полную группу, то сумма вероятностей этих событий равна единице:

По главной диагонали матрицы перехода стоят вероятности 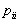того, что система не выйдет из состояния, а останется в нем.

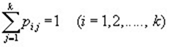
Ц.П.Т. Ляпунова

Пусть выполнены базовые предположения Ц.П.Т. Линдеберга. Пусть случайные величины 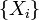имеют конечный третий момент. Тогда определена последовательность

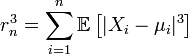. Если предел

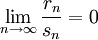(условие Ляпунова),

то

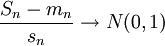по распределению при .

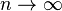Элементы комбинаторного анализа.

Основные правила комбинаторики. Правило умножения (основная теорема комбинаторики).Общее число N способов, которыми можно получить упорядоченную совокупность (a₁,a₂,...a_k), где a_iÎA_i (т.е. выбрать по одному элементу из каждой группы и расставить их в определенном порядке), равно

.

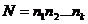Б. Правило сложения. Если один элемент из группы A_i можно выбрать n_i способами, и при этом любые две группы A_i и A_j не имеют обших элементов, то выбор одного элемента или из A₁, или из A₂, ..., или из A_k можно осуществить

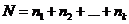способами.

размещения– это упорядоченные совокупности k элементов из n, отличающиеся друг от друга либо составом, либо порядком элементов.

Например. Пусть имеется множество 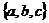из трех элементов. Тогда все размещения двух элементов из трех таковы: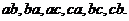

Перестановки – это упорядоченные совокупности, отличающиеся друг от друга только порядком элементов.

Число всех перестановок множества из n элементов обозначается 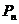и вычисляется по формуле

.

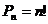сочетания– это неупорядоченные совокупности элементов, отличающиеся друг от друга только составом элементов.

Например.Все сочетания без повторений двух элементов из множества :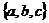

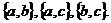
Формула для вычисления числа сочетаний n элементов по k: