Основы теории массового обслуживания
Оренбургский филиал
Федерального государственного бюджетного образовательного учреждения высшего образования
«Поволжский государственный университет телекоммуникаций и информатики»
Кафедра Математических и естественно – научных дисциплин
«УТВЕРЖДАЮ»
Директор ОФ ПГУТИ
____________Преснов А.А._
подпись, Фамилия И.О.
« ____ » ______________ 2016 г.
Горбачев Д. В.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
по выполнению контрольной работы
по теме: «Расчет характеристик системы массового обслуживания»
ПО УЧЕБНОЙ ДИСЦИПЛИНЕ
Основы теории массового обслуживания
для направления подготовки 11.03.02 - Инфокоммуникационные технологии и системы связи
Обсуждено на заседании кафедры
«_____» ____________________ 2016 г.
протокол № ___________
Оренбург 2016 г.
Содержание
Марковские цепи в экономике........................................................................ 3
1. Потоки событий.................................................................................. 6
2. Уравнения Колмогорова.................................................................. 10
3. Системы массового обслуживания.................................................. 16
Классификация систем массового обслуживания.............................. 16
Одноканальная СМО с отказами........................................................ 18
Многоканальная СМО с отказами...................................................... 24
Одноканальная СМО с ожиданием и ограничением на длину очереди 30
Одноканальная СМО с ожиданием..................................................... 36
Многоканальная СМО с ожиданием и ограничением на длину очереди 41
Многоканальная СМО с ожиданием................................................... 47
Рекомендации по оформлению контрольной работы................................. 54
Задания для практических работ и самостоятельной подготовки.............. 54
Список литературы....................................................................................... 56
Марковские цепи
Задача 8.1
На одну телефонную линию поступает простейший поток вызовов с интенсивностью l=0,5 вызовов в минуту. Производительность телефонной линии m=0,3 вызовов в минуту (поток обслуживания простейший). Вызов, поступивший в момент занятости телефонной линии, получает отказ.
Определить:
· Предельные значения относительной пропускной способности, абсолютной пропускной способности и вероятности отказа;
· Среднее время обслуживания одного вызова;
· Вероятность того, что канал свободен;
· Вероятность того, что канал занят;
· Вероятность того, что за 3 мин придёт хотя бы один вызов;
· Вероятность того, что за 5 мин придёт не менее четырёх вызовов.
Решение:
В условиях задачи математической моделью телефонной линии является одноканальная СМО с отказами, имеющая своими параметрами:
интенсивность входящего потока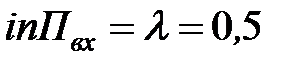 
(выз./мин);
интенсивность потока обслуживаний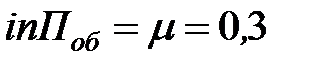 
(выз./мин).
Определим предельную вероятность отказа:
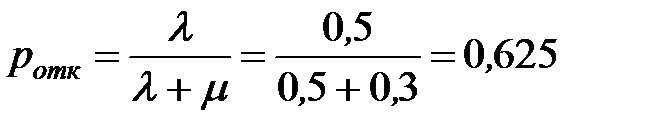или 62,5% - то есть в установившемся предельном режиме из 100 заявок в среднем 63 получит отказ.
Определим предельное значение относительной пропускной способности:
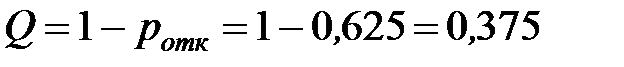или 37,5% - то есть в установившемся предельном режиме из 100 заявок в среднем 38 будут обслужены.
Определим предельное значение абсолютной пропускной способности:
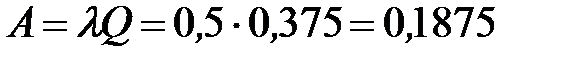- то есть в установившемся предельном режиме абсолютная пропускная способность 0,1875 разговоров в минуту (в 1,6 раза меньше производительности телефонной линии).
Определим среднее время обслуживания одного вызова:
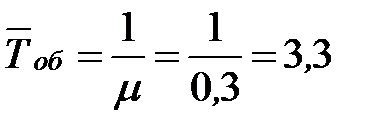- то есть в установившемся предельном режиме среднее время обслуживания одного вызова составляет 3,3 минуты.
Определим среднее время простоя канала:
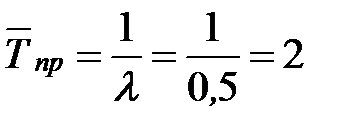- то есть в установившемся предельном режиме среднее время простоя канала составляет 2 минуты.
Определим вероятность того, что канал свободен:
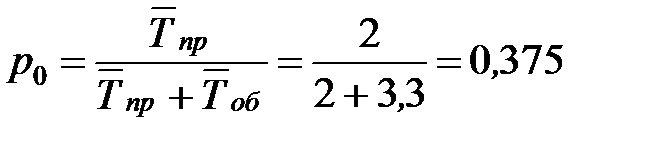или 
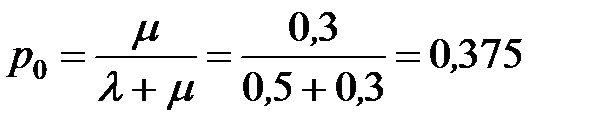
Определим вероятность того, что канал занят:
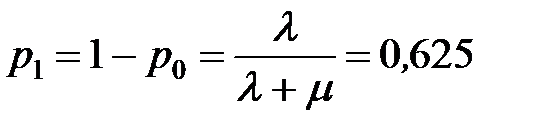или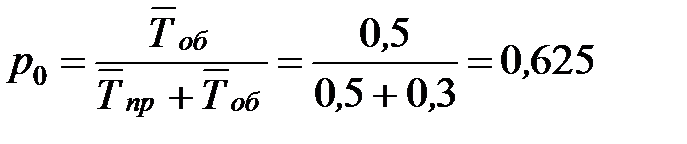 
Таким образом, вероятность того, что канал занят, больше вероятности того, что он свободен. Этого и следовало ожидать, поскольку интенсивность входящего потока l=0,5 больше производительности канала m=0,3.
Контрольные вопросы
1. Что представляет собой промежуток времени между двумя соседними заявками потока обслуживания?
2. Что представляет собой промежуток времени между двумя соседними заявками выходящего потока?
3. Как ведёт себя интенсивность простейшего потока с течением времени?
4. Чему равна интенсивность простейшего входящего потока для одноканальной СМО с отказами?
5. Чему равна интенсивность простейшего потока обслуживаний для одноканальной СМО с отказами?
6. Чему равна вероятность обслуживания заявки для одноканальной СМО с отказами?
7. Чему равна относительная пропускная способность для одноканальной СМО с отказами?
8. Чему равна абсолютная пропускная способность для одноканальной СМО с отказами?
9. От чего зависят вероятности состояний в предельном режиме функционирования СМО?
10. Как можно интерпретировать предельную вероятность состояния СМО?
Задача 8.2
В мастерской бытового обслуживания работают 3 мастера. Если клиент заходит в мастерскую, когда все мастера заняты, то он уходит не ожидая обслуживания. Среднее число клиентов, обращающихся за 1 час, равно 15. Среднее время, которое затрачивает мастер на обслуживание клиента, 5 мин.
Определить основные характеристики эффективности функционирования данной мастерской в предельном режиме и:
· Вероятность того, что клиент получит отказ;
· Вероятность того, что клиент будет обслужен;
· Среднее число клиентов, обслуживаемых мастерской за час;
· Среднее число занятых мастеров.
Решение:
В условиях задачи математической моделью мастерской является многоканальная СМО с отказами, имеющая своими параметрами:
число каналов n=3;
интенсивность входящего потока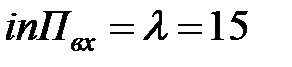 
(чел./час);
среднее время обслуживания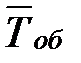 
=5 мин;
интенсивность потока обслуживаний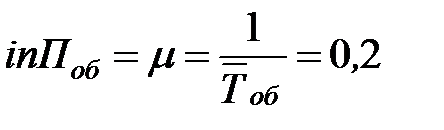 
(чел./мин)=12 (чел./час);
показатель нагрузки СМО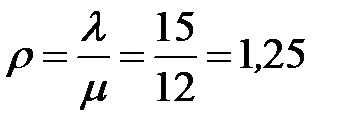 
(эрланга).
Вычисление предельных вероятностей состояний проведём в таблице 8.6.
· вероятность того, что все мастера свободны т.е. р0=0,2979.
· вероятность того, что только один мастер занят т.е. р1=0,3724.
· вероятность того, что два мастера заняты т.е. р2=0,2327.
· вероятность того, что все три мастера заняты т.е. р3=0,0970.
Вероятность того, что клиент получит отказ равна вероятности отказа,равна вероятности того, что заняты все три мастера, т.е. р3=0,0970.
Таблица 8.6 - Расчёт предельных вероятностей состояний
| Значения случайной величины k (число занятых мастеров) |  |  |  |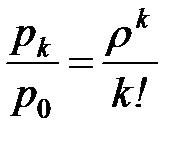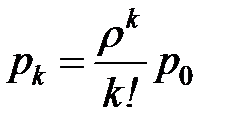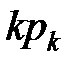
| 0,2979 | |||
| 1,25 | 0,3724 | 0,3724 | |
| 0,7813 | 0,2327 | 0,4655 | |
| 0,3255 | 0,0970 | 0,2909 | |
| S | 3,3568 | 1,0000 | 1,1288 |
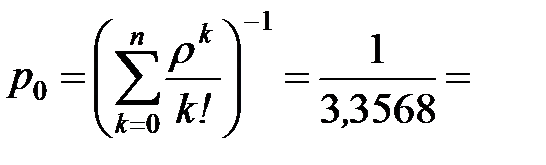 | 0,2979 |
Вычислим вероятность того, что клиент будет обслужен или вычислим относительную пропускную способность мастерской:
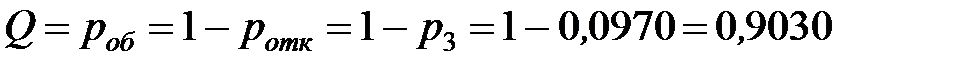- то есть в установившемся предельном режиме из 100 человек, обратившихся в мастерскую в среднем 10 получат отказ, а 90 будут обслужены.
Определим предельное значение абсолютной пропускной способности:
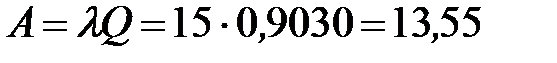- то есть в установившемся предельном режиме среднее число клиентов, обслуживаемых за 1 час составляет 14 человек.
Таким образом оптимальное финансовое решение об организации мастерской должно приниматься с учётом затрат на содержание каждого мастера и потерь в доходе, связанных с необслуженными клиентами.
Контрольные вопросы
1. Кем была впервые выполнена задача исследования многоканальной СМО с отказами?
2. Графом какого процесса является размеченный граф состояний n-канальной СМО с отказами?
3. Что собой представляет приведённая интенсивность входящего потока заявок?
4. Чему равна приведённая интенсивность входящего потока заявок для многоканальной СМО с отказами?
5. Чему равна относительная пропускная способность для многоканальной СМО с отказами?
6. Чему равна абсолютная пропускная способность для многоканальной СМО с отказами?
7.Чему равна интенсивность выходящего потока обслуженных заявок для многоканальной СМО с отказами?
Задача 8.3
На АЗС имеется одна колонка. Площадка при станции, на которой машины ожидают заправку, вмещает не более трёх машин одновременно и, если она занята, то очередная машина, прибывшая к станции, в очередь не становится, а уезжает дальше. Машины прибывают на станцию каждые 2 минуты. Процесс заправки одной машины продолжается в среднем 2,5 минуты.
Определить:
· Вероятность отказа;
· Относительную и абсолютную пропускные способности СМО;
· Среднее число машин, ожидающих заправки;
· Среднее время ожидания машины в очереди;
· Среднее время ожидания машины на АЗС.
Решение:
В условиях задачи математической моделью АЗС является одноканальная СМО с ожиданием и ограничением на длину очереди, имеющая своими параметрами:
ограничение на длину очереди m=3;
интенсивность входящего потока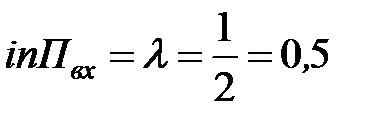 
(маш./мин);
среднее время обслуживания одной машины 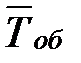=2,5 мин;
интенсивность потока обслуживаний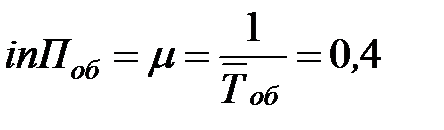 
(маш./мин);
показатель нагрузки СМО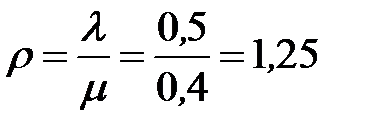 
(эрланга).
Определим предельную вероятность отказа:
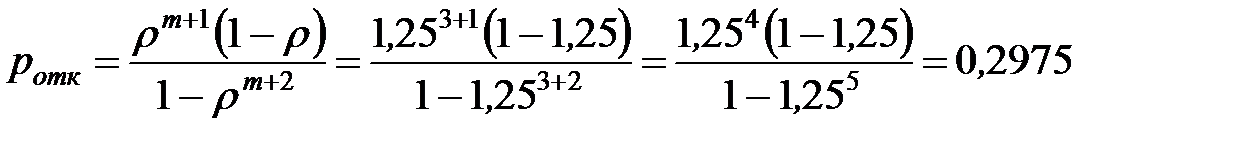или 29,75% - то есть в установившемся режиме из 100 машин в среднем 30 машин получит отказ.
Определим значение относительной пропускной способности:
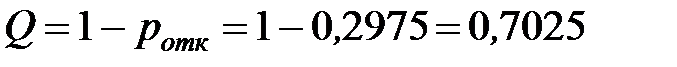или 70,25% - то есть в установившемся режиме из 100 машин в среднем 70 машин будет обслужена, т.е. обслуживается 2/3 всех заявок.
Определим значение абсолютной пропускной способности:
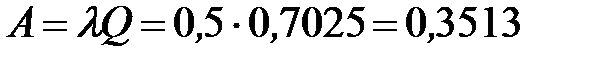- то есть в установившемся режиме абсолютная пропускная способность 0,3513 машин в минуту.
Определим среднее число заявок в очереди:
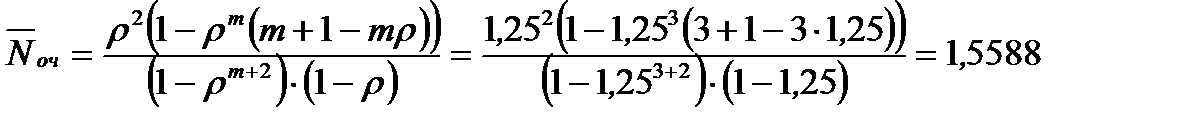- то есть в установившемся режиме среднее число машин, ожидающих в очереди на заправку равно двум машинам.
Определим среднее число заявок, находящихся под обслуживанием:
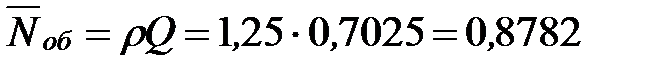- то есть в установившемся режиме среднее число машин, находящихся под обслуживанием равно одной машине. То есть среднее число машин, ожидающих в очереди на заправку практически в два раза выше, чем среднее число машин, находящихся под обслуживанием.
Определим среднее число заявок, находящихся в системе:
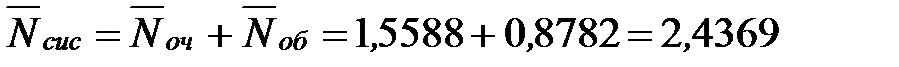- то есть в установившемся режиме среднее число машин, связанных с АЗС равно двум машинам.
Определим среднее время ожидания заявки в очереди:
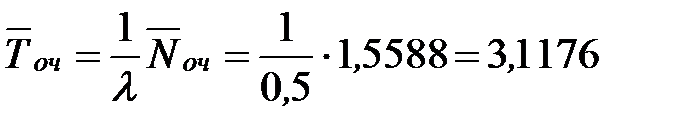- то есть в установившемся режиме среднее время ожидания машины в очереди составляет 3,1 минуты.
Определим среднее время пребывания заявки в СМО:
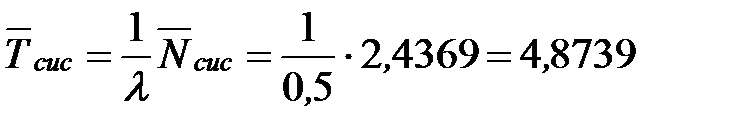- то есть в установившемся режиме среднее время, проведённое машиной на станции, составляет 4,9 минуты.
Определим среднее время обслуживания одной заявки, относящееся ко всем заявкам, как к обслуженным, так и получившим отказ:
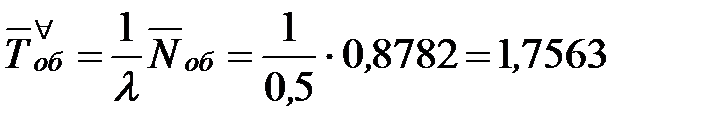- то есть в установившемся режиме среднее время обслуживания одной машины относящееся ко всем машинам – обслуженным и необслуженным, составляет 1,8 минуты.
Таким образом, необходимо либо сократить время обслуживания одной машины (увеличить интенсивность потока обслуживаний), либо увеличить число колонок, либо увеличить площадку для ожидания. Оптимальное решение принимается с учётом затрат, связанных соответственно с увеличением штата обслуживания персонала (увеличение производительности канала), с расширением площадки для ожидания или приобретения дополнительной колонки, и потерь, связанных с потерей заявок на обслуживание.
Контрольные вопросы
1. Чему равно число состояний одноканальной СМО с ограничением на длину очереди в m заявок?
2. Чему равны предельные вероятности состояний системы для одноканальной СМО с числом мест в очереди m и единичной приведённой интенсивностью?
3. Чему равна вероятность отказа для одноканальной СМО с числом мест в очереди m и единичной приведённой интенсивностью?
4. Чему равно среднее число заявок под обслуживанием для одноканальной СМО с ограниченном числом мест в очереди m?
5. Чему равно среднее время ожидания заявки в очереди для одноканальной СМО с ограниченном числом мест в очереди m?
6. Чему равно среднее время нахождения заявки в СМО для одноканальной СМО с ограниченном числом мест в очереди m?
7. Чему равно среднее время обслуживания одной заявки в СМО для одноканальной СМО с ограниченном числом мест в очереди m?
Задача 8.4
Железнодорожную станцию дачного посёлка обслуживает касса с одним окном. В выходные дни, когда население активно пользуется железной дорогой, интенсивность потока пассажиров составляет 0,4 (чел./мин) кассир затрачивает на обслуживание пассажира в среднем 2 мин.
Определить вероятности состояний СМО и основные характеристики эффективности функционирования данной железнодорожной кассы:
· Среднее число пассажиров у кассы;
· Среднее число пассажиров в очереди;
· Среднее время, затрачиваемое пассажиром на приобретение билета;
· Среднее время, ожидания пассажира в очереди.
Решение:
В условиях задачи математической моделью железнодорожной кассы является одноканальная СМО с ожиданием без ограничений на длину очереди и на время ожидания, имеющая своими параметрами:
число каналов n=1;
интенсивность входящего потока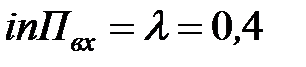 
(чел./мин);
среднее время обслуживания 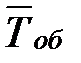=2 мин;
интенсивность потока обслуживаний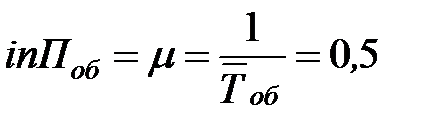 
(чел./мин);
показатель нагрузки СМО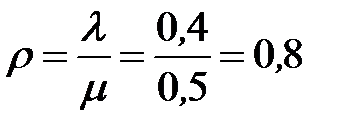 
(эрланга).
Так как l=0,4<m=0,5, или нагрузка на систему r=0,8<1, то предельный режим устанавливается и предельные вероятности состояний существуют.
Определим вероятности состояний СМО:
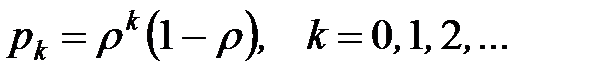
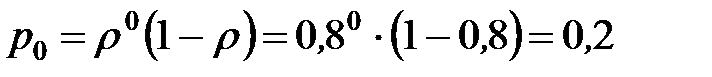- вероятность того, что у кассы нет ни одного человека, или, что кассир свободен;
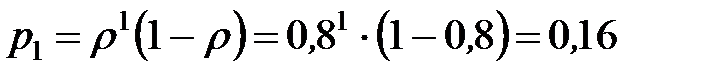- вероятность того, что у кассы один пассажир;
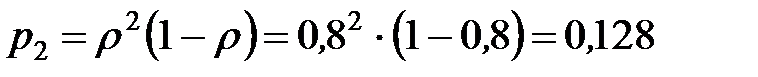- вероятность того, что у кассы два пассажира;
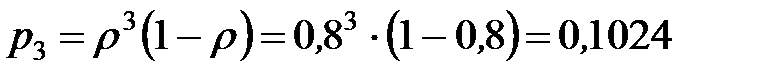- вероятность того, что у кассы три пассажира и т.д.
Определим среднее число заявок в системе:
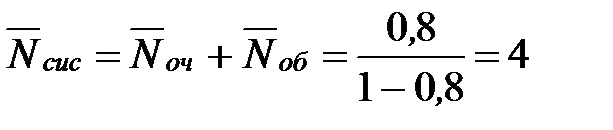- то есть в установившемся предельном режиме среднее число пассажиров у кассы 4 человека – это среднее число пассажиров под обслуживанием и в очереди.
Определим среднее число заявок в очереди:
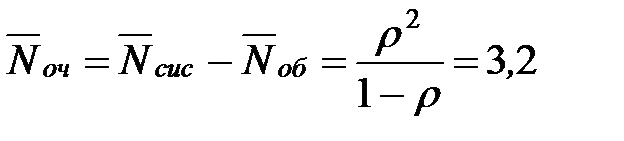- то есть в установившемся предельном режиме среднее число пассажиров находящихся в очереди равно 3 человека.
Определим среднее время пребывания заявки в системе (как в очереди, так и под обслуживанием):
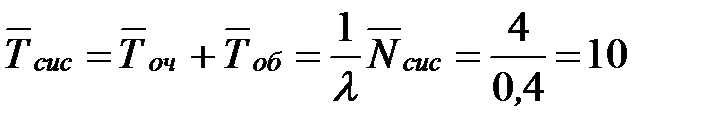- то есть в установившемся предельном режиме среднее время, которое затрачивает пассажир на приобретение билета, складывающееся из среднего времени обслуживания и среднего времени пребывания в очереди составляет 10 минут.
Определим среднее время ожидания заявки в очереди:
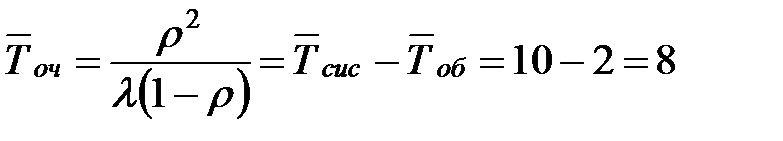- то есть в установившемся предельном режиме среднее время пребывания пассажира в очереди составляет 8 минут, что в четыре раза превышает времени его обслуживания.
Таким образом, чтобы успеть на выбранную электричку, пассажир должен учесть не только время, которое он затрачивает на дорогу до станции, но и подсчитанное время, затрачиваемое на приобретение билета.
Контрольные вопросы
1. Чему равна абсолютная пропускная способность для одноканальной СМО с ожиданием?
2. Чему равна относительная пропускная способность для одноканальной СМО с ожиданием?
3. Что собой представляет среднее число заявок в системе для одноканальной СМО с ожиданием?
4. Чему равна интенсивность выходящего потока заявок для одноканальной СМО с ожиданием?
5. Чему равно среднее число заявок под обслуживанием для одноканальной СМО с ожиданием?
6. Когда существует предельный режим функционирования для одноканальной СМО с ожиданием?
7. Чему равно среднее время пребывания заявки в системе для одноканальной СМО с ожиданием?
Задача 8.5
На АЗС имеется четыре колонки. Площадка при станции, на которой машины ожидают заправку, вмещает не более трёх машин одновременно и, если она занята, то очередная машина, прибывшая к станции, в очередь не становится, а уезжает дальше. Машины прибывают на станцию с интенсивностью 0,6 машина в минуту. Интенсивность процесса обслуживания 0,4 машины в минуту. Определить:
· Вероятность того, что все колонки свободны;
· Вероятность отказа в обслуживании;
· Относительную и абсолютную пропускные способности СМО;
· Среднее число машин, находящихся на обслуживании;
· Среднее число машин, ожидающих заправки;
· Среднее число машин на станции;
· Среднее время ожидания машины в очереди;
· Среднее время пребывания машины на АЗС;
· Среднее время обслуживания одной машины, относящееся ко всем машинам, как к обслуженным, так и получившим отказ.
Решение:
В условиях задачи математической моделью АЗС является многоканальная СМО с ожиданием и ограничением на длину очереди, имеющая своими параметрами:
число каналов обслуживания n=4; ограничение на длину очереди m=3;
интенсивность входящего потока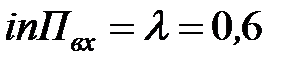 
(маш./мин);
интенсивность потока обслуживаний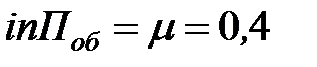 
(маш./мин);
показатель нагрузки СМО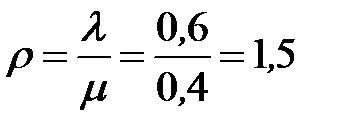 
(эрланга);
показатель нагрузки, приходящийся на один канал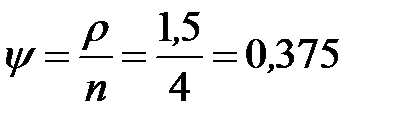 
.
Определим вероятность того, что все каналы свободны (вероятность простаивания всей системы):
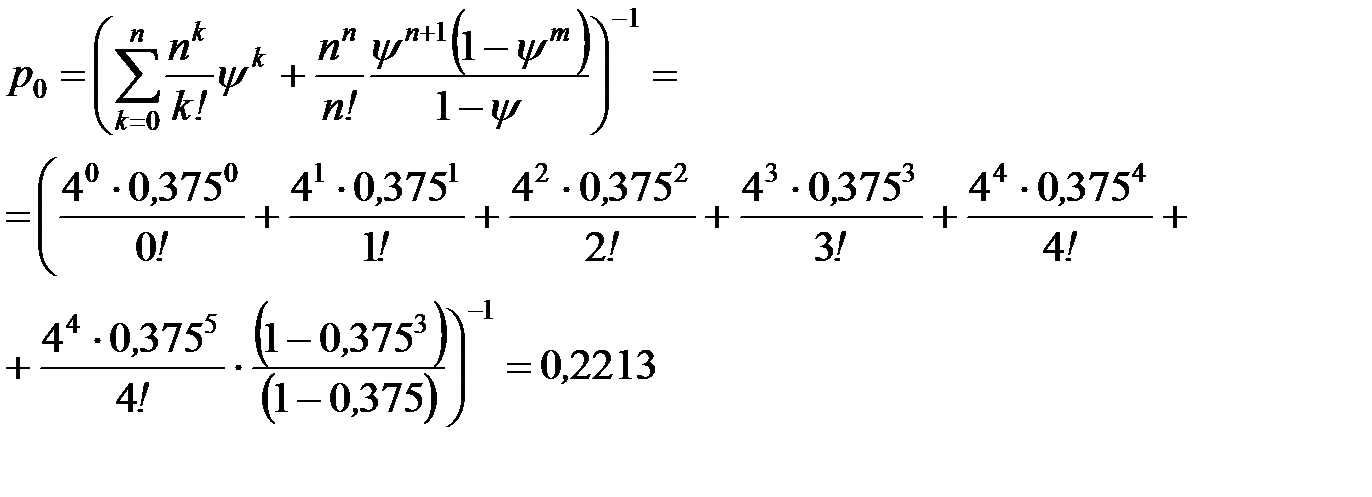
- то есть в вероятность того, что все колонки свободны равна 0,2213.
Находим вероятность отказа в обслуживании:
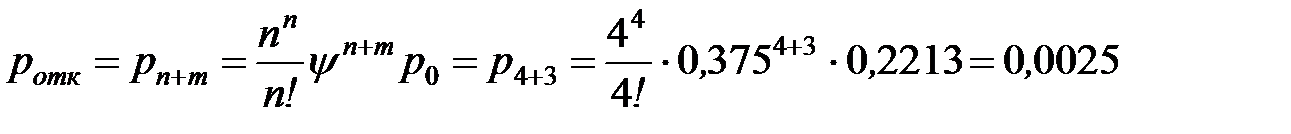
- то есть в вероятность отказа в обслуживании (когда заправляются 4 машины и в очереди 3 машины) равна 0,0025.
Определим значение относительной пропускной способности:
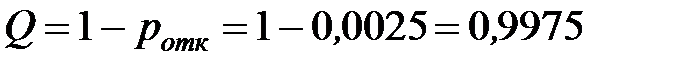или 99,75% - то есть в установившемся режиме из 100 машин практически все будут обслужены.
Определим значение абсолютной пропускной способности:
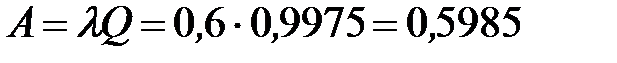- то есть в установившемся режиме абсолютная пропускная способность 0,5985 машин в минуту.
Определим среднее число заявок, находящихся под обслуживанием:
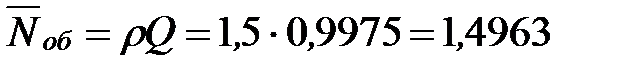- то есть в установившемся режиме среднее число машин, находящихся под обслуживанием равно одной машине.
Определим среднее число заявок в очереди:
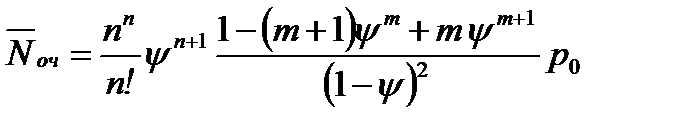
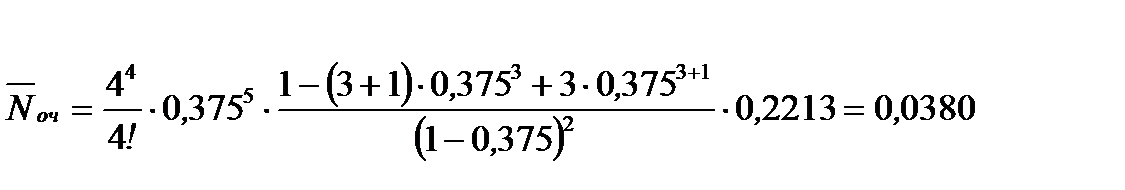
- то есть в установившемся режиме среднее число машин, ожидающих заправки равно 0.
Определим среднее число заявок, находящихся в системе:
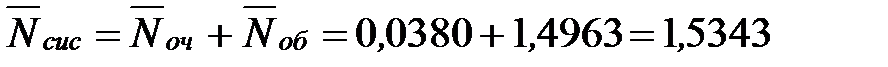- то есть в установившемся режиме среднее число машин, связанных с АЗС равно двум машинам.
Определим среднее время ожидания заявки в очереди:
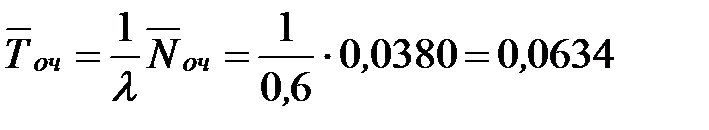- то есть в установившемся режиме среднее время ожидания машины в очереди составляет 0,1 минуты.
Определим среднее время пребывания заявки в СМО:
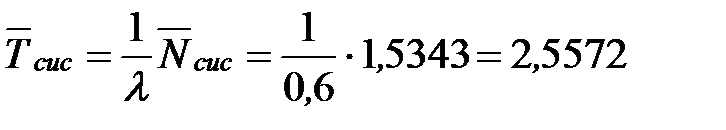- то есть в установившемся режиме среднее время, проведённое машиной на станции, составляет 2,6 минуты.
Определим среднее время обслуживания одной заявки, относящееся ко всем заявкам, как к обслуженным, так и получившим отказ:
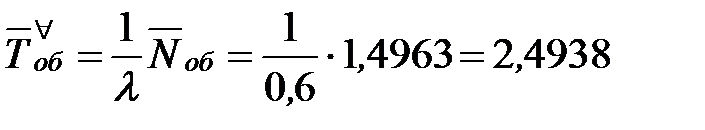- то есть в установившемся режиме среднее время обслуживания одной машины относящееся ко всем машинам – и обслуженным, и необслуженным, составляет 2,5 минуты.
Контрольные вопросы
1. Чему равно число состояний системы для n-канальной СМО с ограничением на длину очереди в m заявок?
2. Когда существуют предельные вероятности состояний для одноканальной для n-канальной СМО с ограничением на длину очереди в m заявок?
3. Чему равна вероятность отказа для n-канальной СМО с ограничением на длину очереди в m заявок?
4. Чему равна вероятность того, что очереди нет для n-канальной СМО с ограничением на длину очереди в m заявок?
5. Чему равна вероятность нахождения в очереди r заявок для n-канальной СМО с ограничением на длину очереди в m заявок?
6. Какие номера принимает время ожидания в очереди для n-канальной СМО с ограничением на длину очереди в m заявок?
7. Чему равна абсолютная пропускная способность для n-канальной СМО с ограничением на длину очереди в m заявок?
Задача 8.6
В кассе метрополитена, продающей жетоны на проезд, имеется два окна. Время, которое тратит кассир на обслуживание одного пассажира, в среднем равно 0,5 мин. Пассажиры подходят к кассе в среднем по 3 чел./мин).
Определить вероятности состояний СМО и основные характеристики эффективности функционирования данной кассы в предельном режиме:
· Среднее число занятых кассиров;
· Среднее число пассажиров в очереди;
· Среднее число пассажиров у касс;
· Среднее время, которое пассажир проводит в очереди;
· Среднее время, которое пассажир тратит на приобретение жетона.
Решение:
В условиях задачи математической моделью кассы метрополитена является многоканальная СМО с ожиданием без ограничений на длину очереди и на время ожидания, имеющая своими параметрами:
число каналов n=2;
интенсивность входящего потока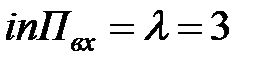 
(чел./мин);
среднее время обслуживания 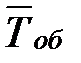=0,5 мин;
интенсивность потока обслуживаний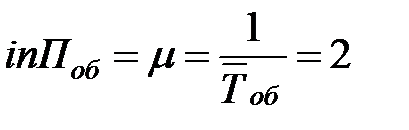 
(чел./мин);
показатель нагрузки СМО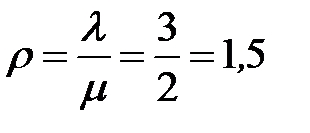 
(эрланга);
показатель нагрузки, приходящийся на один канал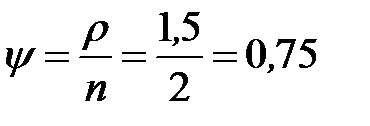 
(эрланга).
Так как l=3<nm=4, или нагрузка на один канал y=0,75<1, то предельный режим устанавливается и предельные вероятности состояний существуют.
Определим вероятность того, что все каналы свободны (вероятность простаивания всей системы):
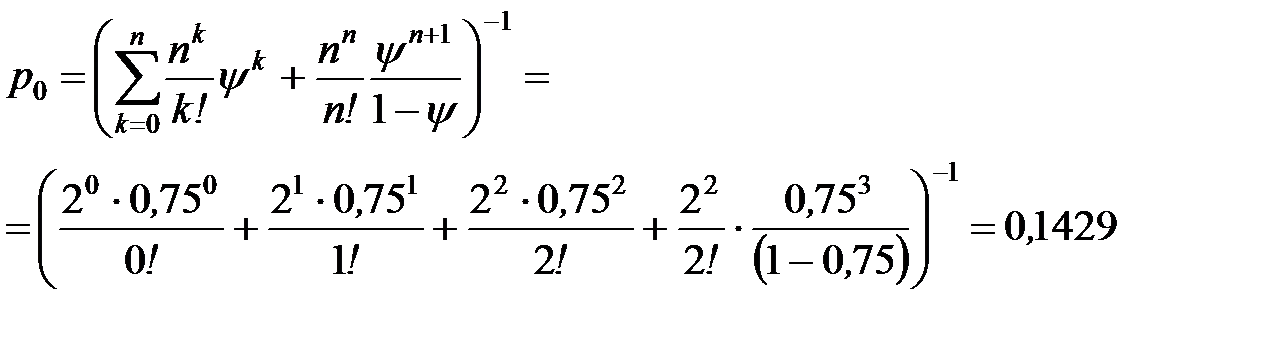
- то есть в вероятность того, что оба кассира свободны или того, что у кассы нет ни одного пассажира равна 0,1429.
Определим вероятность состояний СМО:
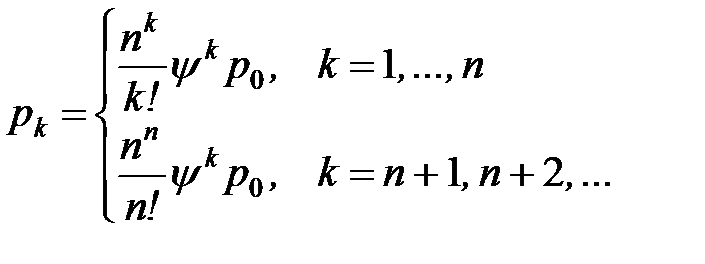
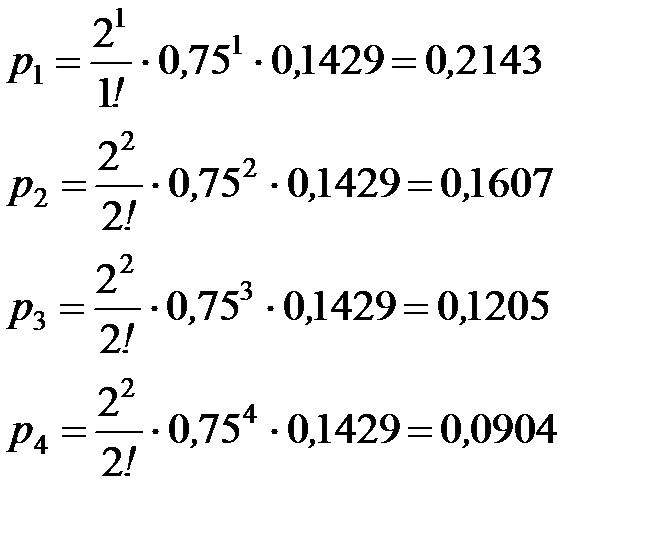
- то есть в вероятности того, что у касс:
1 пассажир равна 0,2143;
2 пассажира равна 0,1607;
3 пассажира равна 0,1205;
4 пассажира равна 0,0904 и т.д.
Аналогично можно рассчитать следующие вероятности (занесём их в таблицу 8.15):
Таблица 8.1
| Вероятности состояний | Рассчитанные значения | Вероятности состояний | Рассчитанные значения | |
| р0 | 0,1429 | р11 | 0,0121 | |
| р1 | 0,2143 | р12 | 0,0091 | |
| р2 | 0,1607 | р13 | 0,0068 | |
| р3 | 0,1205 | р14 | 0,0051 | |
| р4 | 0,0904 | р15 | 0,0038 | |
| р5 | 0,0678 | р16 | 0,0029 | |
| р6 | 0,0509 | р17 | 0,0021 | |
| р7 | 0,0381 | р18 | 0,9973 | |
| р8 | 0,0286 | р19 | 0,0012 | |
| р9 | 0,0215 | р20 | 0,0009 | |
| р10 | 0,0161 | итого | 0,9973®1 |
Определим число занятых каналов – среднее число заявок, находящихся под обслуживанием:
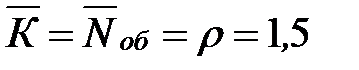- то есть в установившемся режиме среднее число занятых кассиров или среднее число пассажиров под обслуживанием составляет 2 человека.
Определим среднее число заявок в очереди:
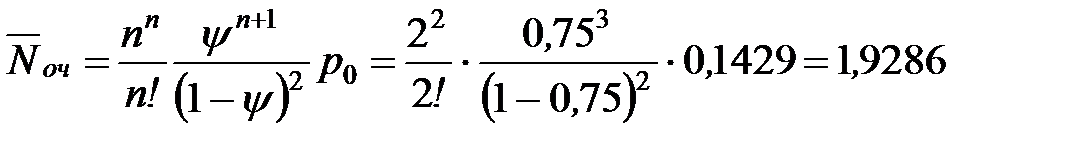
- то есть в установившемся режиме среднее число пассажиров в очереди равно двум.
Определим среднее число заявок, находящихся в системе:
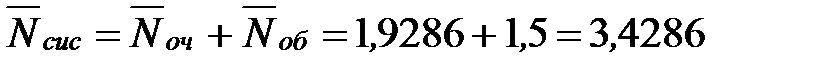- то есть в установившемся режиме среднее число пассажиров у касс равно трём.
Определим среднее время ожидания заявки в очереди:
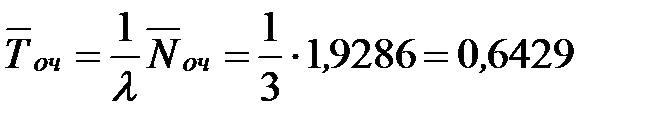- то есть в установившемся режиме среднее время ожидания пассажира в очереди составляет 0,6 минуты.
Определим среднее время пребывания заявки в СМО:
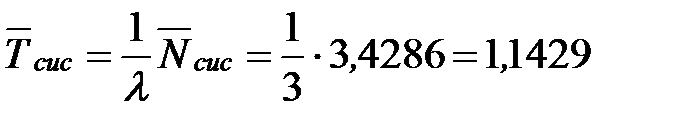- то есть в установившемся режиме среднее время, которое тратит пассажир на приобретение билета, составляет 1,1 минуты.
Итак, рассмотрены некоторые виды СМО. В рекомендуемой литературе следует ознакомиться самостоятельно и разобрать задачи по другим СМО.
Контрольные вопросы
1. Чему равно число состояний для n-канальной СМО с ожиданием?
2. Когда существуют предельные вероятности состояний для n-канальной СМО с ожиданием?
3. Чему равно среднее число заявок под обслуживанием n-канальной СМО с ожиданием?
4. Чему равно среднее число занятых каналов для n-канальной СМО с ожиданием?
5. При каких условиях вероятность отказа равна нулю для n-канальной СМО с ожиданием?
6. При каких условиях вероятность того, что пришедшая заявка будет принята в систему равна 1 для n-канальной СМО с ожиданием?
7. Чему равна абсолютная пропускная способность для n-канальной СМО с ожиданием?
Рекомендации по оформлению контрольной работы
Выбор варианта для решения задач выбирается исходя из последней цифры зачетной книжки. Решить необходимо 4 задачи. Задачи необходимо решить в рабочей тетради самостоятельно. Решение представить преподавателю во время семестра.
На практических и лабораторных занятиях решения задач автоматизируются с помощью пакета прикладных программ: MathCAD, MathLab, MS Excel.
Отчет представляется в виде файла проекта MathCAD, MathLab, MS Excel.
Задания для контрольной работы
Задача № 1
Одноканальная телефонная линия. Заявка-вызов, поступившая в момент, когда линия занята, получает отказ. Простейший поток заявок поступает с интенсивностью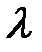 
звонков/ч. Время обслуживания заявки есть случайная величина, которая подчиняется экспоненциальному закону распределения. Средняя продолжительность разговора 
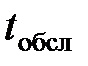мин. Изобразить структуру СМО и размеченный граф состояний, найти предельные вероятности состояний. Определить числовые характеристики и показатели эффективности работы системы.
| вариант | ||||||||||
| | ||||||||||
| |
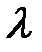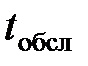Задача № 2
Многоканальная телефонная линия. Заявка-вызов, поступившая в момент, когда все n канала заняты, получает отказ. Простейший поток заявок поступает с интенсивностью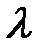 
звонков/ч. Время обслуживания заявки есть случайная величина, которая подчиняется экспоненциальному закону распределения. Средняя продолжительность разговора 
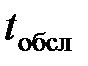мин. Изобразить структуру СМО и размеченный граф состояний, найти предельные вероятности состояний. Определить числовые характеристики и показатели эффективности работы системы.
| вариант | ||||||||||
| | ||||||||||
| | ||||||||||
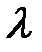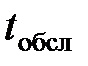| n |
Задача №3
Маленький магазин с одним продавцом. Предполагается, что простейший поток покупателей поступает с интенсивностью 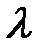человек/ч. Время обслуживания одного покупателя есть случайная величина, которая подчиняется экспоненциальному закону распределения с параметром 
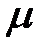человек/ч. При занятости продавца образуется очередь размером m. Изобразить размеченный граф состояний, найти предельные вероятности состояний. Определить числовые характеристики и показатели эффективности работы системы.
Как измениться эффективность работы системы, если в магазине будут работать 2 продавца.
| вариант | ||||||||||
| | ||||||||||
 | ||||||||||
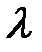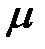| m |
Задача №4
На склад для разгрузки поступает простейший поток грузовиков с интенсивностью 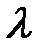грузовиков/ч. Время обслуживания одного грузовика есть случайная величина, которая подчиняется экспоненциальному закону распределения. Средняя продолжительность разгрузки одного грузовика 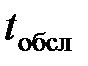мин. Количество терминалов для разгрузки n. Размер стоянки ограничен числом m. Изобразить структуру СМО и размеченный граф состояний, найти предельные вероятности состояний. Определить числовые характеристики и показатели эффективности работы системы.
| вариант | ||||||||||
| | ||||||||||
| | ||||||||||
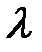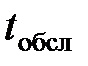| n | ||||||||||
| m |
Список литературы
Основная литература
1. Советов Б. Я. Моделирование систем : учеб. пособие / Б. Я. Советов, С. А. Яковлев. – М. : Высшая школа, 2009. – 344 с.
2. Вентцель Е.С, Овчаров Л.А. Теория вероятностей и ее инженерные приложения. / Е.С. Вентцель, Л.А. Овчаров. – М.: Высш.шк., 2008. – 480 с.
3. Тихоненко О. М. Модели массового обслуживания в информационных системах: Учебное пособие для вузов / О.М. Тихоненко – Минск: «Технопринт», 2003. – 326 с.
Дополнительная литература
1. Клейнрок Л. Теория массового обслуживания. Пер. с англ. – М.: Машиностроение, 1979. – 254 с.
2. Бусленко Н. П. Моделирование сложных систем : учеб. пособие / Н. П. Бусленко. – М. : Наука, 1968. – 356 с.
[1] Теоретически в общем случае система определяется как целостное множество взаимосвязанных элементов, которое нельзя расчленить на независимые подмножества.
[2] Потоком событий (в данном случае, заявок) называют последовательность событий, наступающих одно за другим в какие-то заранее неизвестные, случайные моменты времени.
[3] Случайным процессом (или случайной функцией) называется соответствие, при котором каждому значению аргумента (в данном случае — моменту из промежутка времени проводимого опыта) ставится в соответствие случайная величина (в данном случае — состояние СМО).
[4] Случайный процесс, протекающий в СМО, называется марковским (или процессом без последействия, или процессом без памяти), если вероятность любого состояния СМО в будущем зависит только от ее состояния в настоящем и не зависит от.ее состояний в прошлом.
[5] Поток событий, обладающий свойствами отсутствия последействия (для любых двух непересекающихся промежутков времени число событий, наступающих за один из них, не зависит от числа событий, наступающих за другой) и ординарностью (вероятность наступления за элементарный — малый промежуток времени более одного событий пренебрежимо мала по сравнению с вероятностью наступления за этот промежуток времени одного события), называется пуасооновским.
[6] Вообще, для многоканальной СМО