Задачи нечеткого упорядочения
Любую задачу принятия решений можно сформулировать как задачу отыскания максимального элемента в множестве альтернатив с заданным в нем отношением предпочтения. Однако во многих реальных ситуациях в множестве альтернатив можно определить лишь нечеткое отношение предпочтения, т.е. указать для каждой пары альтернатив 
и 
лишь степени, с которыми выполняются предпочтения 
и 
. В таких случаях задача принятия решения становится неопределенной, поскольку неясно, что такое максимальный элемент для нечеткого отношения предпочтения. Для двух типов нечетких отношенийможно предложить способы упорядочения элементов конечного множества, в котором задано нечеткое отношение. Способы эти сводятся к тому, что для каждого из рассматриваемых типов нечетких отношений строится некоторая функция (напоминающая функцию полезности), и элементы множества упорядочиваются по соответствующим им значениям этой функции.
Пусть 
— функция принадлежности бинарного нечеткого отношения в множестве 
(например, отношения нестрого предпочтения). Допустим, что рассматривается задача упорядочения элементов конечного множества 
. Упорядочение можно осуществлять по значениям следующей функции:
где 
, а функция
Для вычисления значений функции 
удобно пользоваться следующим равенством:
По отношению к этому упорядочению максимальным в множестве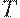 
является элемент 
такой, что
Рассмотрим еще одну задачу упорядочения, иллюстрируемую следующим примером.
Требуется решить, кто из детей: старший сын 
, младший сын 
или дочь 
больше всего похож на отца 
. Заданы "результаты измерений": и взятые отдельно, похожи на отца со степенями 
и 
соответственно; и , взятые отдельно, похожи на отца со степенями 
и 
; наконец, и , взятые отдельно, похожи на отца со степенями и 
.
Таким образом, в этой задаче, в отличие от предыдущей, имеется стандартный элемент (шаблон) для упорядочиваемогомножества 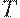, т.е. элемент, обладающий свойствами, общими для всех элементов этого множества. Иначе говоря, если — нечеткое отношение в 
(например, отношение сходства), то
При наличии стандартного элемента для каждой пары элементов и множества 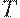задаются величины 
, 
, т.е. степени отношения (например, сходства) и , взятых отдельно, к . Упорядочение элементовмножества 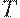с заданным таким способом нечетким отношением предлагается осуществлять в соответствии со значениями функции
Максимальным в смысле этого упорядочения является элемент такой, что
Для задачи о сходстве отца и детей значения этой функции таковы:
Отсюда вытекает, что наиболее похож на отца старший сын, затем следуют дочь и младший сын.
Нейронные сети
Введение
На заре развития электронно-вычислительной техники в середине ХХ века среди ученых и конструкторов еще не существовало единого мнения о том, как должна быть реализована и по какому принципу работать типовая электронно-вычислительная машина. Это сейчас общепринятой является архитектура машины фон Неймана, по которой построены практически все существующие сегодня компьютеры. При этом в тех же учебниках ни слова не говорится о том, что в те же годы были предложены принципиально иные архитектуры и принципы действия компьютеров. Одна из таких схем получила название нейросетевого компьютера, или просто нейросети.
Нейросетевой подход к созданию искусственного интеллекта состоит в проектировании механизмов имитации процесса передачи сигналов в биологическом мозге. Первый интерес к нейросетям был обусловлен пионерской работой МакКаллока и Питса, изданной в 1943 году, где предлагалась схема компьютера, основанного на аналогии с работой человеческого мозга. Они создали упрощенную модель нервной клетки – нейрон. На рис. 1 изображена упрощенная модель биологического мозга. Мозг человека состоит из белого и серого веществ: белое – это тела нейронов, а серое – это соединительная ткань между нейронами, или аксоны и дендриты.
Нейрон состоит из тела и отростков, обычно одного длинного отростка - АКСОНА и нескольких коротких разветвленных отростков ‑ ДЕНДРИТОВ. Аксоны и дендриты соединяют нейроны друг с другом с целью передачи сигналов. По дендритам импульсы следуют к телу клетки, по аксону ‑ от тела клетки к другим нейронам. Место соединения аксонов и дендритов называется СИНАПСОМ.
Биологический мозг состоит из огромного числа (примерно 1011) нейронов, связанных между собой. Нейроны действуют как процессоры передачи сигнала, каждый нейрон получает информацию через свои дендриты, а передает ее дальше – к другим нейронам только через единственный аксон, разветвляющийся на конце на тысячи синапсов.
Простейший нейрон может иметь до 10000 дендритов, принимающих сигналы от других клеток.
Таким образом, мозг содержит примерно 1015 взаимосвязей. Если учесть, что любой нейрофизиологический процесс активизирует сразу множество нейронов, то можно представить себе то количество информации или сигналов, которое возникает в мозгу.
Нейроны взаимодействуют посредством серий импульсов, длящихся несколько миллисекунд, каждый импульс представляет собой частотный сигнал с частотой от нескольких единиц до сотен герц. Это невообразимо медленно по сравнению с современными компьютерами, но в тоже время человеческий мозг гораздо быстрее машины может обрабатывать аналоговую информацию, как-то: узнавать изображения, чувствовать вкус, узнавать звуки, читать чужой почерк, оперировать качественными параметрами. Все это реализуется посредством сети нейронов, соединенных между собой синапсами. Другими словами, мозг -–это система из параллельных процессоров, работающая гораздо эффективнее, чем популярные сейчас последовательные вычисления.
Что из себя представляет нейронная сеть (НС)? Исходя из названия — сеть представляет из себя совокупность нейронов, соединенных друг с другом определенным образом. Каждый нейрон представляет из себя элемент, который вычисляет выходной сигнал (по определенному правилу) из совокупности входных сигналов. То есть основная последовательность действий одного нейрона такая:
· Прием сигналов от предыдущих элементов сети
· Комбинирование входных сигналов
· Вычисление выходного сигнала
· Передача выходного сигнала следующим элементам нейронной сети
Между собой нейроны могут быть соединены абсолютно по-разному, это определяется структурой конкретной сети. Но суть работы нейронной сети остается всегда одной и той же. По совокупности поступающих на вход сети сигналов на выходе формируется выходной сигнал (или несколько выходных сигналов). То есть нейронную сеть упрощенно можно представить в виде черного ящика, у которого есть входы и выходы. А внутри этого ящика сидит огромное количество нейронов.
Эту упрощенную модель можно считать метафорой для представления искусственных нейронных сетей (ИНС), осуществляемого с использованием электрических и электронных аппаратных средств и программного обеспечения, как показано на рис. 2.
В теории ИНС обычно опускается такой компонент нейрона, как дендрит и считается, что входами ячейки нейрона являются непосредственно Синапсы, а выходом – аксон.
Далее под нейроном будет подразумеваться искусственный нейрон, то есть ячейка нейронной сети (НС). Нейрон характеризуется своим состоянием и, по аналогии с реальным нейроном, может быть либо возбуждён — либо заторможен.
Нейрон обладает группой синапсов – однонаправленных входных связей, соединенных с выходами других нейронов, а также имеет аксон – выходную связь данного нейрона, с которой сигнал (возбуждения или торможения) поступает на синапсы следующих нейронов. Общий вид нейрона приведен на рисунке 3. Каждый синапс характеризуется величиной синаптической связи или ее весом wi
По физическому смыслу, вес синоптической связи – это электрическая проводимость данного синапса.
Текущее состояние нейрона определяется, как взвешенная сумма его входов:
Значение на входе синапса умножается на вес данного синапса, потом все эти значения суммируются и получаем текущее состояние нейрона.
МакКаллок и Питтс [W.S. McCulloch and W. Pitts, "A logical Calculus of Ideas Immanent in Nervous Activity", Bull. Mathematical Biophysics, Vol. 5, 1943, pp. 115-133] предложили использовать бинарный пороговый элемент в качестве модели искусственного нейрона. Этот математический нейрон вычисляет взвешенную сумму n входных сигналов xj, j = 1, 2... n, и формирует на выходе сигнал величины 1, если эта сумма превышает определенный порог u, и 0 - в противном случае.
Часто удобно рассматривать u как весовой коэффициент, связанный с постоянным входом x0 = 1. Положительные веса соответствуют возбуждающим связям, а отрицательные - тормозным. МакКаллок и Питтс доказали, что при соответствующим образом подобранных весах совокупность параллельно функционирующих нейронов подобного типа способна выполнять универсальные вычисления. Здесь наблюдается определенная аналогия с биологическим нейроном: передачу сигнала и взаимосвязи имитируют аксоны и дендриты, веса связей соответствуют синапсам, а пороговая функция отражает активность сомы.
Выход нейрона есть функция его состояния: Y = F(S)
Нелинейная функция F называется активационной и может иметь различный вид, как показано на рисунке 4.
Рис.4 а) функция единичного скачка; б) линейный порог (гистерезис);
в) сигмоид – гиперболический тангенс; г) сигмоид – формула (3)
Одной из наиболее распространенных является нелинейная функция с насыщением, так называемая логистическая функция или сигмоид (т.е. функция S-образного вида):
При уменьшении a сигмоид становится более пологим, в пределе при a=0 вырождаясь в горизонтальную линию на уровне 0.5, при увеличении a сигмоид приближается по внешнему виду к функции единичного скачка с порогом T в точке x=0. Из выражения для сигмоида очевидно, что выходное значение нейрона лежит в диапазоне [0,1].
Одна из причин, по которой сигмоид используется в нейронных сетях, это простое выражение его производной через саму функцию (которое и позволило существенно сократить вычислительную сложность метода обратного распространения ошибки, сделав его применимым на практике):
Вычисление производной необходимо, потому что для корректировки весовых коэффициентов при обучении ИНС с помощью алгоритма обратного распространения, используется метод градиентного спуска.
Формально, искусственный нейрон – является однослойным перцептроном (персептроном), т.е. моделью, в которой входные элементы напрямую соединены с выходными с помощью системы весов, и выполняет функцию линейной классификации.
Классификация – это процесс группировки/разбиения объектов исследования или наблюдения в соответствии с их общими признаками.
Линейный классификатор — это один из самых простых алгоритмов классификации.
В задачах с двумя классами (бинарная классификация) линейный классификатор — это гиперплоскость, разделяющая n-мерное пространство признаков на два класса (полупространства). Т.е. нейрон (линейный классификатор) определяет — входные данные относятся либо к группе A, либо к группе B. Это можно представить, если рассмотреть линию в 2-мерном пространстве. Точки в этом пространстве могут быть классифицированы, как лежащие либо по одну сторону этой линии, либо по другую.
Однослойный перцептрон хорош для решения задач линейной классификации, т.е. именно для случая двумерного пространства и классифицирующей линии, но он не сможет решить задачу, которая не может быть решена линейным разделением.
Классический пример задачи, которая не по зубам однослойному перцептрону — исключающее ИЛИ (XOR — exclusive OR).
Рис.5 Однонейронный перцептрон
Однослойный перцептрон, состоящий из одного нейрона с двумя входами, представленный на рисунке 5, не способен разделить плоскость (двумерное гиперпространоство) на две полуплоскости так, чтобы осуществить классификацию входных сигналов по классам 0 и 1 в соответствии с логической функцией XOR.
Рассмотрим точки (0,0), (1,0), (0,1), и (1,1) в пространстве.
Для XOR, не существует способа провести одну линию, которая отделяет точки TRUE: (1,0) и (0,1) от точек FALSE: (0,0) и (1,1).
Т.о. точки XOR линейно неразделимы.Выходит, однослойный перцептрон не может быть обучен, для разделения по XOR. Чтобы решить проблему XOR, нужно создать многослойный перцептрон!
Архитектура нейронных сетей
ИНС может рассматриваться как направленный граф со взвешенными связями, в котором искусственные нейроны являются узлами. По архитектуре связей ИНС могут быть сгруппированы в два класса (рис. 5): сети прямого распространения, в которых графы не имеют петель, и рекуррентные сети, или сети с обратными связями.
Сеть РБФ (радиально-базисных функций) — искусственная нейронная сеть, которая использует радиальные базисные функции как функции активации.
АРТ ‑ Адаптивная резонансная теория, сети адаптивного резонанса — разновидность искусственных нейронных сетей основанная на теории адаптивного резонанса Стивена Гроссберга и Гейла Карпентера. Включает в себя модели, использующие обучение с учителем и без учителя и используются при решении задач распознавания образов и предсказания.
Нейронные сети различают по:
· структуре сети (связей между нейронами);
· особенностям модели нейрона;
· особенностям обучения сети.
По структуре нейронные сети можно разделить (рисунок 8) на:
· неполносвязные (или слоистые) и полносвязные;
· со случайными и регулярными связями;
· с симметричными и несимметричными связями.
Рисунок 8 – Классификация нейронных сетей по структуре
Неполносвязные нейронные сети (описываемые неполносвязным ориентированным графом и обычно называемые перцептронами), подразделяются на однослойные (простейшие перцептроны) и многослойные, с прямыми, перекрестными и обратными связями. В нейронных сетях с прямыми связями нейроны j-ого слоя по входам могут соединяться только с нейронами i-ых слоев, где j > i , т.е. с нейронами нижележащих слоев. В нейронных сетях с перекресными связями допускаются связи внутри одного слоя, т.е. выше приведенное неравенство заменяется на j > = i . В нейронных сетях с обратными связями используются и связи j-ого слоя по входам с i-ым при j < i.
С точки зрения топологии можно выделить три основных типа нейронных сетей:
· полносвязные (рисунок 9, а);
· многослойные или слоистые (рисунок 9, б);
· слабосвязные (с локальными связями) (рисунок 9, в).
Рисунок 9 – Архитектуры нейронных сетей: а – полносвязная сеть, б – многослойная сеть с последовательными связями, в – слабосвязные сети
В полносвязных нейронных сетях каждый нейрон передает свой выходной сигнал остальным нейронам, в том числе и самому себе. Все входные сигналы подаются всем нейронам. Выходными сигналами сети могут быть все или некоторые выходные сигналы нейронов после нескольких тактов функционирования сети.
В многослойных нейронных сетях нейроны объединяются в слои. Слой содержит совокупность нейронов с едиными входными сигналами. Число нейронов в слое может быть любым и не зависит от количества нейронов в других слоях. В общем случае сеть состоит из Q слоев, пронумерованных слева направо. Внешние входные сигналы подаются на входы нейронов входного слоя (его часто нумеруют как нулевой), а выходами сети являются выходные сигналы последнего слоя. Кроме входного и выходного слоев в многослойной нейронной сети есть один или несколько скрытых слоев. Связи от выходов нейронов некоторого слоя q к входам нейронов следующего слоя (q+1) называются последовательными.
В свою очередь, среди многослойных нейронных сетей выделяют следующие типы.
1) Монотонные. Это частный случай слоистых сетей с дополнительными условиями на связи и нейроны. Каждый слой кроме последнего (выходного) разбит на два блока: возбуждающий и тормозящий. Связи между блоками тоже разделяются на тормозящие и возбуждающие. Если от нейронов блока А к нейронам блока В ведут только возбуждающие связи, то это означает, что любой выходной сигнал блока является монотонной неубывающей функцией любого выходного сигнала блока А. Если же эти связи только тормозящие, то любой выходной сигнал блока В является невозрастающей функцией любого выходного сигнала блока А. Для нейронов монотонных сетей необходима монотонная зависимость выходного сигнала нейрона от параметров входных сигналов.
2) Сети без обратных связей. В таких сетях нейроны входного слоя получают входные сигналы, преобразуют их и передают нейронам первого скрытого слоя, и так далее вплоть до выходного, который выдает сигналы для интерпретатора и пользователя. Если не оговорено противное, то каждый выходной сигнал q-гo слоя подастся на вход всех нейронов (q+1)-гo слоя; однако возможен вариант соединения q-гo слоя с произвольным (q+p)-м слоем.
Среди многослойных сетей без обратных связей различают полносвязанные (выход каждого нейрона q-гo слоя связан с входом каждого нейрона (q+1)-гo слоя) и частично полносвязанные. Классическим вариантом слоистых сетей являются полносвязанные сети прямого распространения (рисунок 10).
Рисунок 10 – Многослойная (двухслойная) сеть прямого распространения
3) Сети с обратными связями. В сетях с обратными связями информация с последующих слоев передается на предыдущие. Среди них, в свою очередь, выделяют следующие:
· слоисто-циклические, отличающиеся тем, что слои замкнуты в кольцо: последний слой передает свои выходные сигналы первому; все слои равноправны и могут как получать входные сигналы, так и выдавать выходные;
· слоисто-полносвязанные состоят из слоев, каждый из которых представляет собой полносвязную сеть, а сигналы передаются как от слоя к слою, так и внутри слоя; в каждом слое цикл работы распадается на три части: прием сигналов с предыдущего слоя, обмен сигналами внутри слоя, выработка выходного сигнала и передача к последующему слою;
· полносвязанно-слоистые, по своей структуре аналогичные слоисто-полносвязанным, но функционирующим по-другому: в них не разделяются фазы обмена внутри слоя и передачи следующему, на каждом такте нейроны всех слоев принимают сигналы от нейронов как своего слоя, так и последующих.
В качестве примера сетей с обратными связями на рисунке 11 представлены частично-рекуррентные сети Элмана и Жордана.
Рисунок 11 – Частично-рекуррентные сети: а – Элмана, б – Жордана
В слабосвязных нейронных сетях нейроны располагаются в узлах прямоугольной или гексагональной решетки. Каждый нейрон связан с четырьмя (окрестность фон Неймана), шестью (окрестность Голея) или восемью (окрестность Мура) своими ближайшими соседями.
Известные нейронные сети можно разделить по типам структур нейронов на:
· гомогенные (однородные);
· гетерогенные.
Гомогенные сети состоят из нейронов одного типа с единой функцией активации, а в гетерогенную сеть входят нейроны с различными функциями активации.
Еще одна классификация делит нейронные сети на:
· синхронные;
· асинхронные.
В первом случае в каждый момент времени лишь один нейрон меняет свое состояние, во втором – состояние меняется сразу у целой группы нейронов, как правило, у всего слоя. Алгоритмически ход времени в нейронных сетях задается итерационным выполнением однотипных действий над нейронами.
По используемым на входах и выходах сигналам нейронные сети можно разделить на:
· аналоговые;
· бинарные.
Бинарные оперируют только двоичными сигналами, и выход каждого нейрона может принимать значение либо логического ноля (заторможенное состояние) либо логической единицы (возбужденное состояние).
По моделированию времени нейронные сети подразделяются на сети:
· с непрерывным временем;
· с дискретным временем.
Для программной реализации применяется как правило дискретное время.
По способу подачи информации на входы нейронной сети различают:
· подачу сигналов на синапсы входных нейронов;
· подачу сигналов на выходы входных нейронов;
· подачу сигналов в виде весов синапсов входных нейронов;
· аддитивную подачу на синапсы входных нейронов.
По способу съема информации с выходов нейронной сети различают:
· съем с выходов выходных нейронов;
· съем с синапсов выходных нейронов;
· съем в виде значений весов синапсов выходных нейронов;
· аддитивный съем с синапсов выходных нейронов.
По организации обучения разделяют обучение нейронных сетей:
· с учителем (supervised neural networks);
· без учителя (nonsupervised).
При обучении с учителем предполагается, что есть внешняя среда, которая предоставляет обучающие примеры (значения входов и соответствующие им значения выходов) на этапе обучения или оценивает правильность функционирования нейронной сети и в соответствии со своими критериями меняет состояние нейронной сети или поощряет (наказывает) нейронную сеть, запуская тем самым механизм изменения ее состояния.
По способу обучения разделяют обучение:
· по входам
· по выходам.
При обучении по входам обучающий пример представляет собой только вектор входных сигналов, а при обучении по выходам в него входит и вектор выходных сигналов, соответствующий входному вектору.
По способу предъявления примеров различают:
· предъявление одиночных примеров
· предъявление "страницы" примеров.
В первом случае изменение состояния нейронной сети (обучение) происходит после предъявления каждого примера. Во втором – после предъявления "страницы" (множества) примеров на основе анализа сразу их всех.
Под состоянием нейронной сети, которое может изменяться, обычно понимается:
· веса синапсов нейронов (карта весов – map) (коннекционистский подход);
· веса синапсов и пороги нейронов (обычно в этом случае порог является более легко изменяемым параметром, чем веса синапсов);
· установление новых связей между нейронами (свойство биологических нейронов устанавливать новые связи и ликвидировать старые называется пластичностью).
По особенностям модели нейрона различают нейроны с разными нелинейными функциями:
пороговой 
;
Наиболее часто в качестве функций активации используются следующие виды сигмоид:
Функция Ферми (экспоненциальная сигмоида):
Рациональная сигмоида (при 
=0 вырождается в т.н. пороговую функцию активации):
Гиперболический тангенс:
,
где s — выход сумматора нейрона, — произвольная константа.
Перечисленные функции относятся к однопараметрическим.
Также используются многопараметрические передаточные функции, например, 
.
Наиболее распространенные модели нейронных сетей:
· модель Хопфилда;
· машина Больцмана;
· сеть Кохонена;
· модель Хэмминга;
· многослойный персептрон.
Обучение нейронных сетей
Нейронные сети используются для представления знаний. В отличие от обычного вычисления представление знания в нейронных сетях выполняет поиск по содержанию, а не по адресу сохраненных данных. Кроме того, представление знаний в нейронных сетях осуществляется через приблизительное, а не абсолютно точное соответствие. Представление знаний в нейронных сетях состоит из сети, весов связей и семантических интерпретаций, присоединенных к активациям узлов. Например, в контексте управленческой классификации при использовании обученной нейронной сети можно предугадать, выберет ли клиент новый продукт, основываясь на выраженных в числах данных о клиенте, таких как последняя купленная марка, интерес к предварительному экспонированию, возможность дополнительного экспонирования и интерес к нему. Эти кванторные признаки атрибутов являются входами в обученную нейронную сеть. Активация «+1», полученная от нейронной сети, может указывать на то, что клиент выберет новое изделие, а «-1» — наоборот.
Обобщение знаний в нейронных сетях достигается путем обучения. Процесс обучения в нейронных сетях стимулирует желательные образцы активации и блокирует нежелательные, основываясь на доступных данных. Для достижения определенного обобщения знаний в нейронной сети разрабатывается алгоритм обучения. Функция ошибки, определенная на выходе нейронной сети, или энергетическая функция, определенная при активации элементов сети, характеризует качество нейронной сети в обобщении знаний. Обучающий набор данных в этом случае должен состоять из образцов представления знаний, которым предполагается обучить нейронную сеть. Алгоритм обучения действует методом изменения либо весов (т. е. силы связей между узлами), либо выходов нейронной сети, либо структуры нейронной сети, стремясь к минимальным ошибкам или энергии, основываясь на обучающих данных.
В системах нейронных сетей большое количество парадигм обучения. Обучение с учителем (контролируемое обучение) и обучение без учителя (неконтролируемое обучение или самообучение) — вот две главные парадигмы, обычно используемые в проектировании обучающих алгоритмов. Бывает ещё смешанная парадигма.
В парадигме обучения с учителем нейронная сеть располагает правильными ответами (выходами сети) на каждый входной пример. Процесс обучения пытается минимизировать «дистанцию» между фактическими и желаемыми выходами нейронной сети. Веса настраиваются так, чтобы сеть производила ответы как можно более близкие к известным правильным ответам. Усиленный вариант обучения с учителем предполагает, что известна только критическая оценка правильности выхода нейронной сети, но не сами правильные значения выхода.
Противоположностью обучения с учителем является обучение без учителя. В отличие от обучения с учителем здесь не существует априорного набора желаемых значений выхода и не требуется знания правильных ответов на каждый пример обучающей выборки. Когда используется такая парадигма, подразумевается несколько образцов входа. Предполагается, что в процессе обучения нейронная сеть обнаруживает существенные особенности входов (раскрывается внутренняя структура данных или корреляции между образцами в системе данных, что позволяет распределить образцы по категориям). Нейронная сеть должна развить собственное представление стимулов входа без помощи учителя.
При смешанном обучении часть весов определяется посредством обучения с учителем, в то время как остальная получается с помощью самообучения.
Теория обучения рассматривает три фундаментальных свойства, связанных с обучением по примерам: емкость, сложность образцов и вычислительная сложность.
Под емкостью понимается, сколько образцов может запомнить сеть, и какие функции и границы принятия решений могут быть на ней сформированы.
Сложность образцов определяет число обучающих примеров, необходимых для достижения способности сети к обобщению. Слишком малое число примеров может вызвать "переобученность" сети, когда она хорошо функционирует на примерах обучающей выборки, но плохо - на тестовых примерах, подчиненных тому же статистическому распределению.
Известны 4 основных типа правил обучения: коррекция по ошибке, машина Больцмана, правило Хебба и обучение методом соревнования.
Правило коррекции по ошибке. При обучении с учителем для каждого входного примера задан желаемый выход d. Реальный выход сети y может не совпадать с желаемым. Принцип коррекции по ошибке при обучении состоит в использовании сигнала (d-y) для модификации весов, обеспечивающей постепенное уменьшение ошибки. Обучение имеет место только в случае, когда перцептрон ошибается. Известны различные модификации этого алгоритма обучения [J. Hertz, A. Krogh, and R.G. Palmer, Introduction to the Theory of Neural Computation, Addison-Wesley, Reading, Mass., 1991].
Обучение Больцмана. Представляет собой стохастическое правило обучения, которое следует из информационных теоретических и термодинамических принципов [J.A. Anderson and E. Rosenfeld, "Neurocomputing: Foundation of Research", MIT Press, Cambridge, Mass., 1988.]. Целью обучения Больцмана является такая настройка весовых коэффициентов, при которой состояния видимых нейронов удовлетворяют желаемому распределению вероятностей. Обучение Больцмана может рассматриваться как специальный случай коррекции по ошибке, в котором под ошибкой понимается расхождение корреляций состояний в двух режимах.
Правило Хебба. Самым старым обучающим правилом является постулат обучения Хебба [D.O. Hebb, The Organization of Behavior, John Wiley & Sons, New York, 1949.]. Хебб опирался на следующие нейрофизиологические наблюдения: если нейроны с обеих сторон синапса активизируются одновременно и регулярно, то сила синаптической связи возрастает. Важной особенностью этого правила является то, что изменение синаптического веса зависит только от активности нейронов, которые связаны данным синапсом. Это существенно упрощает цепи обучения в реализации VLSI.
Обучение методом соревнования. В отличие от обучения Хебба, в котором множество выходных нейронов могут возбуждаться одновременно, при соревновательном обучении выходные нейроны соревнуются между собой за активизацию. Это явление известно как правило "победитель берет все". Подобное обучение имеет место в биологических нейронных сетях. Обучение посредством соревнования позволяет кластеризовать входные данные: подобные примеры группируются сетью в соответствии с корреляциями и представляются одним элементом.
При обучении модифицируются только веса "победившего" нейрона. Эффект этого правила достигается за счет такого изменения сохраненного в сети образца (вектора весов связей победившего нейрона), при котором он становится чуть ближе ко входному примеру. На рис. 3 дана геометрическая иллюстрация обучения методом соревнования. Входные векторы нормализованы и представлены точками на поверхности сферы. Векторы весов для трех нейронов инициализированы случайными значениями. Их начальные и конечные значения после обучения отмечены Х на рис. 3а и 3б соответственно. Каждая из трех групп примеров обнаружена одним из выходных нейронов, чей весовой вектор настроился на центр тяжести обнаруженной группы.
Рис. N.Пример обучения методом соревнования: (а) перед обучением; (б) после обучения
Можно заметить, что сеть никогда не перестанет обучаться, если параметр скорости обучения не равен 0. Некоторый входной образец может активизировать другой выходной нейрон на последующих итерациях в процессе обучения. Это ставит вопрос об устойчивости обучающей системы. Система считается устойчивой, если ни один из примеров обучающей выборки не изменяет своей принадлежности к категории после конечного числа итераций обучающего процесса. Один из способов достижения стабильности состоит в постепенном уменьшении до 0 параметра скорости обучения. Однако это искусственное торможение обучения вызывает другую проблему, называемую пластичностью и связанную со способностью к адаптации к новым данным. Эти особенности обучения методом соревнования известны под названием дилеммы стабильности-пластичности Гроссберга.
В Таблице 2 представлены различные алгоритмы обучения и связанные с ними архитектуры сетей (список не является исчерпывающим). В последней колонке перечислены задачи, для которых может быть применен каждый алгоритм. Каждый алгоритм обучения ориентирован на сеть определенной архитектуры и предназначен для ограниченного класса задач. Кроме рассмотренных, следует упомянуть некоторые другие алгоритмы:
Adaline и Madaline [R.P.Lippmann, "An Introduction to Computing with Neural Nets", IEEE ASSP Magazine, Vol.4, No.2, Apr. 1987, pp. 4-22.],
линейный дискриминантный анализ], проекции Саммона [A.K. Jain and J. Mao, "Neural Networks and Pattern Recognition", in Computational Intelligence: Imitating Life, J.M. Zurada, R.J. Marks II, and C.J. Robinson, eds., IEEE Press, Piscataway, N.J., 1994, pp. 194-212.],
метод/анализ главных компонентов [J. Hertz, A. Krogh, and R.G. Palmer, Introduction to the Theory of Neural Computation, Addison-Wesley, Reading, Mass., 1991.].
Таблица 2. Известные алгоритмы обучения.
| Парадигма | Обучающее правило | Архитектура | Алгоритм обучения | Задача |
| С учителем | Коррекция ошибки | Однослойный и многослойный перцептрон | Алгоритмы обучения перцептрона Обратное распространение Adaline и Madaline | Классификация образов Аппроксимация функций Предсказание, управление |
| Больцман | Рекуррентная | Алгоритм обучения Больцмана | Классификация образов | |
| Хебб | Многос< Наши рекомендации |