Классификация функций принадлежности нормальных нечеткихмножеств

Нечеткое множество называется нормальным, если для его функции принадлежности 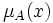справедливоутверждение, что существует такой 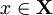, при котором .

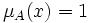Функция принадлежности класса s

Функция принадлежности класса s определяется как:

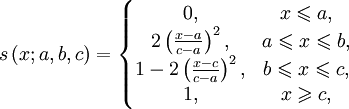
где .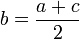

Функция принадлежности класса π

Функция принадлежности класса π определяется через функцию класса s:

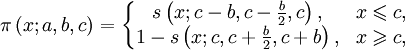
где .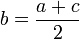

Функция принадлежности класса γ

Функция принадлежности класса γ определяется как:

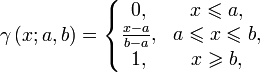
Функция принадлежности класса t

Функция принадлежности класса t определяется как:

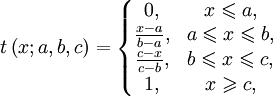
Функция принадлежности класса L

Функция принадлежности класса L определяется как:

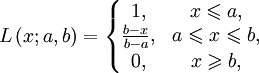
Определим лингвистическую переменную (ЛП) как переменную, значение которой определяется набором словесных характеристик некоторого свойства. Например, ЛП "возраст" может иметь значения

ЛП = МлВ, ДВ, ОВ, ЮВ, МВ, ЗВ, ПВ, СВ ,

обозначающие возраст младенческий, детский, отроческий, юношеский, молодой, зрелый, преклонный и старый, соответственно. Множество M - это шкала прожитых человеком лет [0..120]. Функция принадлежности определяет, насколько мы уверены, что данное количество прожитых лет можно отнести к данному значению ЛП. Допустим, что неким экспертом к молодому возрасту отнесены люди в возрасте 20 лет со степенью уверенности 0,8, в возрасте 25 лет со степенью уверенности 0,95, в возрасте 30 лет со степенью уверенности 0,95 и в возрасте 35 лет со степенью уверенности 0,7. Итак:

μ(X₁)=0,8; μ(X₂)=0,95; μ(X₃)=0,95; μ(X₄)=0,7;

Значение ЛП=МВ можно записать:

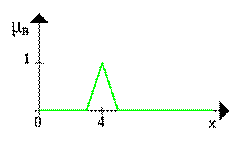
МВ = μ(X₁) / X₁ + μ(X₂) / X₂ + μ(X₃) / X₃ + μ(X₄) / X₄ = = 0,8 / X₁ + 0,95 / X₂ + 0,95 / X₃ + 0,7 / X₄ .

Таким образом, нечеткие множества позволяют учитывать субъективные мнения отдельных экспертов. Для большей наглядности покажем множество МВ графически при помощи функции принадлежности (рис. 2.7).

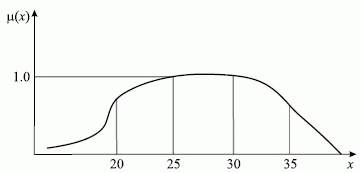
Рис. 2.7. График функции принадлежности

Для операций с нечеткими множествами существуют различные операции, например, операция "нечеткое ИЛИ" (иначе ) задается в логике Заде [39], [40]:

μ(x)=max(μ₁(x), μ₂(x))

и при вероятностном подходе так:

μ(x)=μ₁(x)+μ₂(x)-μ₁(x) · μ₂(x).

Рассмотрим эти операции в виде диаграмм. В ранней статье о нечетких множествах Заде предложил оператор минимума для пересечения и оператор максимума для объединения двух нечетких множеств. Легко видеть, что эти операторы совпадают с четким объединением, и пересечением, если мы рассматриваем только принадлежность к 0 и 1.

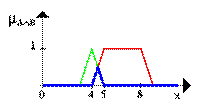
Чтобы разъяснять это, рассмотрим несколько примеров. Допустим А есть нечеткий интервал между 5 и 8, а B - нечеткое число, приблизительно 4. Следующая диаграмма показывает нечеткое множество между 5 и 8 И (AND - пересечение) приблизительно 4 (синия линия).

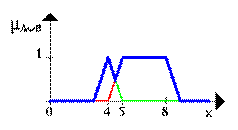
Нечеткое множество между 5 и 8 ИЛИ (OR-объединение) приблизительно 4 показывается в следующей диаграмме (снова, синей линией).

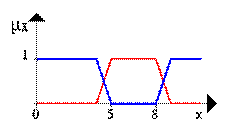
Следующая диаграмма явкяется примером отрицания. Синяя линия - ОТРИЦАНИЕ нечеткого множества A.

Существуют и другие операции над нечеткими числами, такие как расширенные бинарные арифметические операции (сложение, умножение и пр.) для нечетких чисел, определяемые через соответствующие операции для четких чисел с использованием принципа обобщения и т.д.

Baldwin J.F.. Fuzzy logic and fuzzy reasoning. - London, Academic Press, 1981.

Для задания нечеткой истинности Балдвин предложил такие функции принадлежности нечетких "истинно" и "ложно":

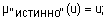
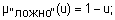
где .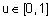

Квантификаторы "более-менее" и "очень" часто применяют к нечеткими множествами "истинно" и "ложно", получая таким образом термы "очень ложно", "более-менее ложно", "более-менее истинно", "очень истинно", "очень, очень истинно", "очень, очень ложно" и т.п. Функции принадлежности новых термов получают, выполняя операции концентрации и растяжения нечетких множеств "истинно" и "ложно". Операция концентрации соответствует возведению функции принадлежности в квадрат, а операция растяжения - возведению в степень ½. Следовательно, функции принадлежности термов "очень, очень ложно", "очень ложно", "более-менее ложно", "более-менее истинно", "истинно", "очень истинно" и "очень, очень истинно" задаются так:

;

;

;

;

.

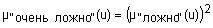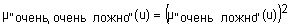
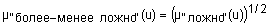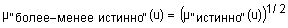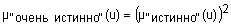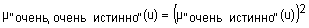Графики функций принадлежности этих термов показаны на рис. 15.

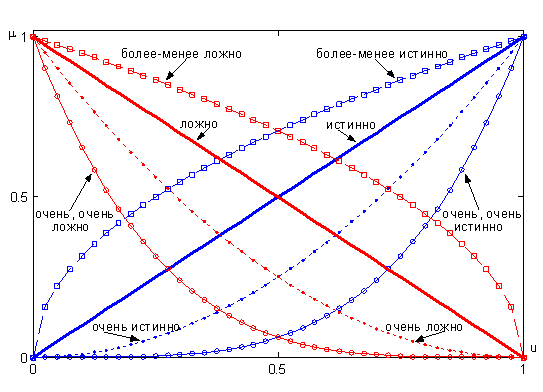
Рисунок 15 - Лингвистическая переменная "истинность" по Балдвину