Решение оптимизационных задач в среде Microsoft Excel
Лабораторный практикум.
Решение оптимизационных задач в среде Microsoft Excel
Методические указания к лабораторным работам по дисциплине
ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ
для всех направлений и специальностей
(квалификация (степень) «специалист», «бакалавр»)
Уфа 2012
УДК 004
ББК
М54
Рекомендовано к изданию методической комиссией факультета информационных технологий и управления (протокол № __ от «__» _______ 2012 г.)
Составитель: к.с.н., доцент Г.Г. Исламова
Рецензент: ст. преп. С.П. Лакеева
Ответственный за выпуск: заведующий кафедрой Информатики и информационных технологий, к.х.н., доц. А.С. Беляева
г. Уфа, БГАУ, Кафедра информатики и информационных технологий
ОГЛАВЛЕНИЕ
| Лабораторная работа №1 Назначение надстройки Поиск решения в электронных таблицах Excel | |
| Лабораторная работа №2 Решение задач линейного программирования методом оптимизации с помощью надстройки Поиск решения | |
| Лабораторная работа №3 Решение транспортных задач методом оптимизации с помощью надстройки Поиск решения | |
| Лабораторная работа №4 Решение задач дискретного программирования методом оптимизации с помощью надстройки Поиск решения | |
| Лабораторная работа №5 Решение задач нелинейного программирования методом оптимизации с помощью надстройки Поиск решения | |
| БИБЛИОГРАФИЧЕСКИЙ СПИСОК | |
| ПРИЛОЖЕНИЕ А | |
| ПРИЛОЖЕНИЕ Б | |
| ПРИЛОЖЕНИЕ В | |
| ПРИЛОЖЕНИЕ Г | |
| ПРИЛОЖЕНИЕ Д |
Лабораторная работа №1
«Назначение надстройки Поиск решения в электронных таблицах Excel»
Цель работы: Овладеть приемами работы с надстройкой Поиск решения в электронных таблицах Excel. Научиться:
ü находить оптимальное решение задачи с помощью надстройки Поиск решения;
ü создавать отчеты по результатам поиска решения;
ü сохранять параметры модели.
1 Общие сведения
1.1 Оптимизационное моделирование в экономике
В сфере управления сложными системами (например, в экономике) применяется оптимизационное моделирование, в процессе которого осуществляется поиск наиболее оптимального пути развития системы.
Критерием оптимальности могут быть различные параметры. Например, в экономике можно стремиться к максимальному количеству выпускаемой продукции, а можно – к ее низкой себестоимости. Оптимальное развитие соответствует экстремальному (максимальному или минимальному) значению выбранного целевого параметра.
Развитие сложных систем зависит от множества факторов, следовательно, значение целевого параметра зависит от множества параметров. Выражением такой зависимости является целевая функция (или функционал качества):
K = F(X1, X2,...,Xn),
где K – значение целевого параметра,
Х1, Х2,..., Хn – параметры, влияющие на развитие системы.
Цель исследования состоит в нахождении экстремума этой функции и определении значений параметров, при которых этот экстремум достигается. Если целевая функция нелинейна, то она имеет экстремумы, которые находятся определенными методами. Однако часто целевая функция линейна и, соответственно, экстремумов не имеет. Задача поиска оптимального режима при линейной зависимости приобретает смысл только при наличии определенных ограничений на параметры. Если ограничения на параметры (система неравенств) также имеют линейный характер, то такие задачи являются задачами линейного программирования. Термин «линейное программирование» в имитационном моделировании понимается как поиск экстремумов линейной функции, на которую наложены ограничения.
Различные аспекты оптимизации занимают очень важное место в бизнесе и деятельности современных организаций и предприятий. Проблемы оптимизации присутствуют в самых различных процессах, которые можно условно разделить на следующие категории:
ü оптимизация перевозок грузов;
ü оптимизация распределения ресурсов;
ü оптимизация расхода/раскроя материалов.
Основным (наиболее часто используемым) способом решения задач оптимизации является, так называемый, симплекс-метод. Универсальность применения симплекс-метода в том, что оптимизация заключается в максимизации или минимизации значения какой-либо целевой функции (например, максимизации прибыли/дохода или минимизации затрат) в условиях выполнения различных ограничений (например, по количеству или стоимости доступных ресурсов).
1.2 Надстройка Поиск решения
Решение задач оптимизации может быть существенно облегчено с помощью надстройки электронной таблицы Excel Поиск решения.Поиск решений является частью блока задач, который иногда называют анализом «что-если». Это процесс изменения значений ячеек на листе и анализа влияния этих изменений на результат вычисления формул, например, изменение процентной ставки, используемой в таблице амортизации для определения сумм платежей.
Процедура поиска решения позволяет найти оптимальное значение формулы, содержащейся в ячейке, которая называется целевой.
Формулировка таких задач может представлять собой систему уравнений с несколькими неизвестными и набор ограничений на решения, поэтому
задачи необходимо начинать с построения соответствующей модели.
1.2.1 Назначение надстройки Поиск решения
Задачами, решаемыми с помощью надстройкиПоиск решения, являются:
ü ассортимент продукции: максимизация выпуска товаров при ограничениях на сырье (или другие ресурсы) для производства изделий;
ü штатное расписание: составление штатного расписания для достижения наилучших результатов при наименьших расходах;
ü планирование перевозок: минимизация затрат на транспортировку;
ü составление смеси: получение заданного количества смеси при наименьших расходах;
ü оптимальный раскрой материалов (ограничения – количество деталей различной формы и размеров);
ü оптимизация финансовых показателей (например, максимизация доходов за счет оптимизации средств на разные инвестиционные проекты).
Задачи, лучше всего решаемые данным средством, имеют три свойства:
ü имеется единственная максимизируемая или минимизируемая цель;
ü имеются ограничения, выражающиеся, как правило, в виде неравенств;
ü имеется набор входных значений-переменных, прямо или косвенно влияющих на ограничения и на оптимизируемые величины.
1.2.2 Ограничения в задачах
Под ограничениями понимаются соотношения типа А1>=В1, А1=А2, А3>=0. По крайней мере, одна из ячеек в соотношении, определяющем ограничение, должна зависеть от переменных задачи, в противном случае это ограничение не может влиять на процесс решения.
Часто ограничения записываются сразу для групп ячеек, например: A1:А10<=В1:В10 или А1:Е1>=0.
Иногда простановка ограничений очень проста, но бывают случаи, когда ограничения менее очевидны и могут быть указаны неверно или даже могут оказаться пропущенными.
Примеры ограничений такого типа:
ü в модели с несколькими периодами времени величина материального ресурса на начало следующего периода должна равняться величине этого ресурса на конец предыдущего периода;
ü в модели поставок величина запаса на начало периода плюс количество полученного должна равняться величине запаса на конец периода плюс количество отправленного;
ü многие величины в модели по своему физическому смыслу не могут быть отрицательными, например, количество полученных единиц товара.
Ограничения и логические формулы воспринимаются надстройкой Поиск решенияпо-разному. В найденном решении логические формулы будут выполнены точно, а ограничения – с некоторой возможной погрешностью. Величина этой погрешности задается параметром «Относительная погрешность», по умолчанию значение этого параметра равно 0,000001.
1.2.3 Виды математических моделей
При решении оптимизационных задач с помощью надстройки «Поиск решения»целесообразно различать линейные и нелинейные модели. Общий вид линейной функции:
Х = А*Y1 + В*Y2 + С*Y3…,
где А, В и С – константы, Y1, Y2, Y3 – переменные, Х – результирующее значение.
Надстройка Поиск решения может решать и оптимизационные задачи, содержащие нелинейные зависимости и ограничения. Нелинейные зависимости могут встречаться довольно часто.
Например, оптимизация графика поставок часто сталкивается с нелинейностью зависимости стоимости одного изделия от объема партии.
1.2.4 Установка надстройки Поиск решения
Для того чтобы установить надстройку Поиск решениянеобходимо:
1) выбрать команду Сервис - Надстройки;
2) в диалоговом окне (рисунок 1.1) установить флажок напротив строки Поиск решения и нажать  .
.
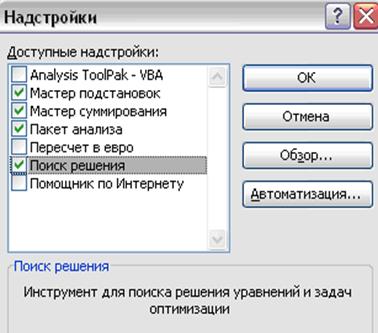
Рисунок 1.1 Подключение надстройки Поиск решения
1.3 Нахождение оптимального решения с помощью надстройки Поиск решения
1.3.1 Последовательность работы с надстройкой Поиск решения
При решении задачи оптимизации для нахождения наилучшего решения необходимо представить модель задачи в виде таблицы на рабочем листе Excel (см. п. 3) и выполнить следующие действия:
1) Выделить оптимизируемую ячейку, например, В20.
2) Выбрать команду Сервис – Поиск решения. При этом появляется диалоговое окно Поиск решения (рисунок 1.2).
3) В поле Установить целевую ячейку уже находится ссылка на выделенную на первом шаге ячейку. При необходимости ссылку можно изменить.
4) Установить тип взаимосвязи между целевой ячейкой и решением путем выбора переключателя (таблица 1.1) в группе Равной (рисунок 1.2).
5) В поле Изменяя ячейки указать ячейки-параметры, которые могут изменяться в процессе поиска решения. Например, $C$8:$G$10.
Кнопка  служит для автоматического поиска ячеек-параметров. При этом в поле Изменяя ячейки попадут все ячейки, не содержащие формулы и влияющие на формулу.
служит для автоматического поиска ячеек-параметров. При этом в поле Изменяя ячейки попадут все ячейки, не содержащие формулы и влияющие на формулу.
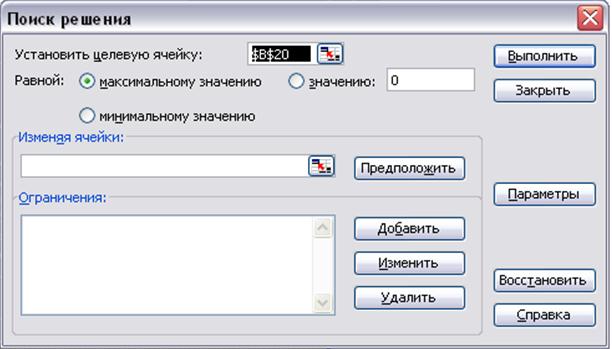
Рисунок 1.2 Диалоговое окно Поиск решения
Таблица 1.1 Переключатели группы Равной
| Переключатель | Описание |
| Максимальному значению | Поиск максимального значения для целевой функции |
| Минимальному значению | Поиск минимального значения для целевой функции |
| Значению | Поиск заданного (фиксированного, рассчитываемого по формуле) значения для целевой ячейки |
6) Нажать на кнопку  для открытия диалогового окна Добавление ограничения, в котором ввести ограничения для задачи (рисунок 1.3).
для открытия диалогового окна Добавление ограничения, в котором ввести ограничения для задачи (рисунок 1.3).
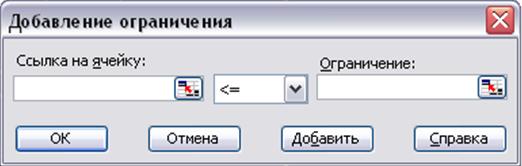
Рисунок 1.3 Диалоговое окно Добавление ограничения
В окне Добавление ограничения можно ввести ограничения следующим образом: в поле Ссылка на ячейку указать соответствующую ячейку или диапазон ячеек, например, $B$8:$B$10, а в поле Ограничения ввести необходимое значение (см. рисунок 1.4). Знак отношения <=, установленный по умолчанию, можно заменить на другой. Помимо ограничений, представимых в виде равенств и неравенств (с помощью знаков >=, <=, =), можно использовать условие целочисленности (Цел). Для ввода нескольких ограничений следует нажать кнопку  .
.
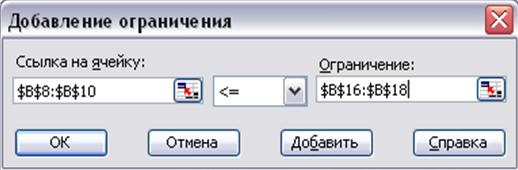
Рисунок 1.4 Заполненное диалоговое окно Добавление ограничения
7) После введения всех ограничений и нажатия на кнопку  , появится заполненное диалоговое окно Поиск решения (рисунок 1.5).
, появится заполненное диалоговое окно Поиск решения (рисунок 1.5).
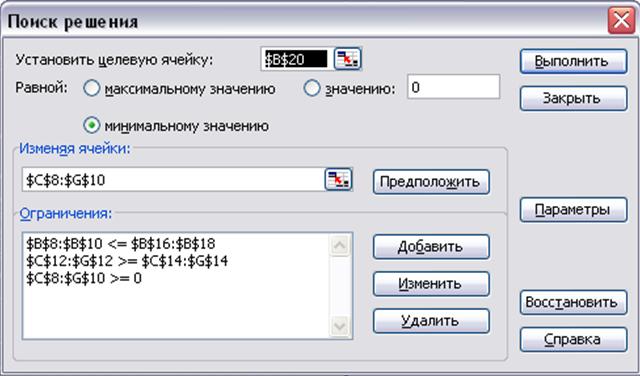
Рисунок 1.5 Пример заполненного окна Поиск решения
Поиск решения позволяет экспериментировать с различными параметрами задачи для определения наилучшего варианта решения. Для изменения ограничений необходимо в диалоговом окне Поиск решения в списке нужное ограничение и нажать кнопку  , произвести изменения и нажать кнопку
, произвести изменения и нажать кнопку  .
.
Для удаления ограничений можно воспользоваться кнопкой  , а кнопка
, а кнопка  позволяет сбросить все параметры в диалоговом окне Поиск решения.
позволяет сбросить все параметры в диалоговом окне Поиск решения.
8) Нажать кнопку  , после чего появиться диалоговое окно Результаты поиска решения (рисунок 1.6).
, после чего появиться диалоговое окно Результаты поиска решения (рисунок 1.6).
9) В окне Результаты поиска решения выбрать один из переключателей Сохранить найденное решение либо Восстановить исходные значения.
В первом случае параметры модели сохраняются на рабочем листе в указываемых пользователем ячейках, во втором – остаются значения, которые были ранее на рабочем листе. Чтобы позднее запустить процесс решения с другими ограничениями, нужно отредактировать необходимые неравенства.
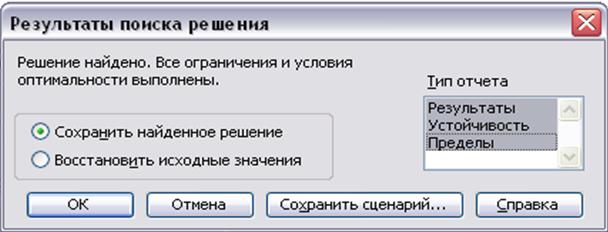
Рисунок 1.6 Диалоговое окно Результаты поиска решения
После того как решение найдено, можно также сохранить ссылки на изменяемые ячейки, чтобы использовать их в составе сценария. Для этого нужно нажать кнопку  (рисунок 1.6) в диалоговом окне Результаты поиска решения.
(рисунок 1.6) в диалоговом окне Результаты поиска решения.
В диалоговом окне Сохранение сценария необходимо ввести имя сценария и нажать кнопку  (рисунок 1.7).
(рисунок 1.7).
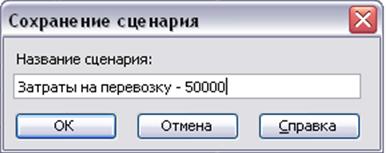
Рисунок 1.7 Диалоговое окно Сохранение сценария
1.3.2 Изменение параметров работы
НадстройкаПоиск решения позволяет изменить параметры работы при поиске решения, например, поменять метод поиска ответа, ограничить время поиска, задать другую точность вычислений. При нажатии кнопки  окна Поиск решения появляется диалоговое окно Параметры поиска решения (рисунок 1.8).
окна Поиск решения появляется диалоговое окно Параметры поиска решения (рисунок 1.8).
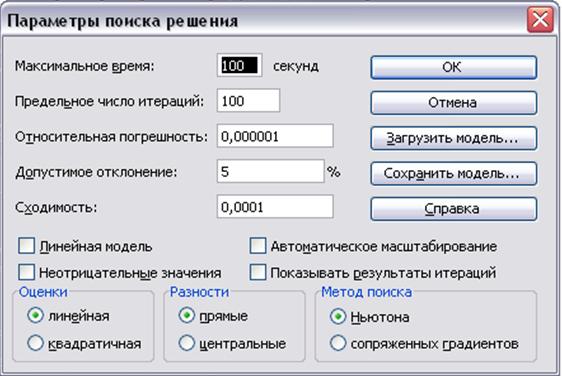
Рисунок 1.8 Диалоговое окно Параметры поиска решения
Установки по умолчанию подходят для решения большинства типов оптимизационных задач. Параметры надстройкиПоиск решенияи их описание приведены в таблице 1.2.
Таблица 1.2 Параметры надстройкиПоиск решения
| Параметр | Описание |
| Максимальное время | Максимальное время в секундах (не превышающее 32767), которое может быть затрачено на поиск решения |
| Предельное число итераций | Максимальное число итераций, которые могут быть сделаны. Итерация – вычисление очередного значения (приближения) и проверка, насколько это значение подходит в качестве ответа |
| Относительная погрешность | Задает точность выполнения ограничений от 0 до 1 |
| Допустимое отклонение | В случае целочисленных ограничений задает, насколько близок (в процентном соотношении) должен быть ответ к возможному наилучшему решению |
| Сходимость | Когда относительное изменение значения в целевой ячейке за последние пять итераций становится меньше числа, указанного в этом поле, поиск прекращается |
| Линейная модель | Ускоряет поиск решения линейной задачи оптимизации или линейной аппроксимации нелинейной задачи путем использования методов линейного программирования |
| Неотрицательные значения | Установление неотрицательности всех переменных, для которых не заданы явные ограничения |
| Показывать результаты итераций | Выводит промежуточный результат и делает паузу при каждой итерации |
| Автоматическое масштабирование | Включение автоматической нормализации входных и выходных значений, качественно различающихся по порядку следования величины |
| Оценки | Выбор линейного или квадратичного метода оценки |
| Разности | Указывает метод численного дифференцирования, который используется для вычисления частных производных целевых или ограничивающих функций |
| Метод поиска | Выбор алгоритма оптимизации или сопряженных градиентов для указания направления поиска |
1.3.3 Создание отчетов по результатам поиска решения
По найденным результатам можно создавать отчеты. Они полезны для сравнения влияния на решение различных ограничений или исходных данных. Отчеты бывают трех типов: Результаты, Устойчивость, Пределы.
Тип выбирается по окончании поиска решения в диалоговом окне Результаты поиска решения в списке Отчеты (рисунок 1.6). Можно выбрать два или три типа отчета щелчком мыши или при нажатой клавише <Ctrl>.
Каждый отчет создается на отдельном листе. После выбора одного или нескольких типов отчетов в рабочей книге Excel появятся листы с соответствующими названиями.
Один из примеров отчета – Результаты – приведен на рисунке 1.9, а содержание отчетов всех типов – в таблице 1.3.
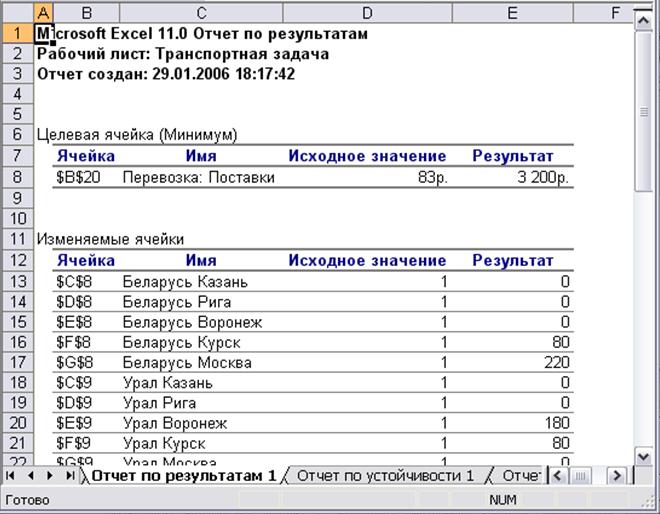
Рисунок 1.9 Пример отчета по решению оптимизационной задачи
Таблица 1.3 Содержание отчетов
| Тип отчета | Содержание |
| Результаты | Состоит из целевой ячейки и списка влияющих ячеек модели, их исходных и конечных значений, а также формул ограничений и дополнительных сведений о наложенных ограничениях |
| Устойчивость | Содержит сведения о чувствительности решения к малым изменениям в формуле модели или в формулах ограничений. |
| Пределы | Состоит из целевой ячейки и списка влияющих ячеек модели, их значений, а также нижних и верхних границ. |
1.3.4 Сохранение параметров модели
Последние использованные параметры модели сохраняются на рабочем листе.
В некоторых случаях желательно иметь несколько наборов параметров. Например, для рассмотрения разных решений при различных ограничениях можно хранить в ячейках рабочего листа и быстро загружать необходимые установки.
Сохранение параметров модели осуществляется с помощью кнопки  в окне Параметры поиска решения.
в окне Параметры поиска решения.
После нажатия этой кнопки в диалоговом окне Сохранить модельнеобходимо указать диапазон ячеек (рисунок 1.10), в которых будут находиться параметры модели. Число выделенных ячеек должно равняться числу ограничений модели плюс три.
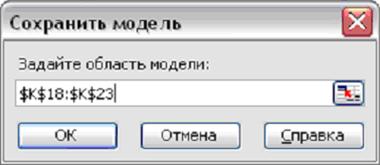
Рисунок 1.10 Диалоговое окно Сохранить модель с указанием диапазона ячеек для сохранения параметров решения
Приняв предлагаемый диапазон или изменив его на другой (например, $K$18:$K$23), необходимо нажать кнопку  .
.
То же самое нужно сделать во вновь появившемся диалоговом окне Параметры поиска решения.
Для получения окончательного результата необходимо нажать кнопку  в диалоговом окне Поиск решения.
в диалоговом окне Поиск решения.
Выбранный диапазон ячеек будет заполнен параметрами модели.
1.3.5 Загрузка параметров модели
При последующем открытии рабочего листа и запуске средства Поиск решения появится диалоговое окно с теми же параметрами, которые были установлены при предыдущем запуске.
Для загрузки сохраненных параметров модели необходимо выполнить следующие действия:
1) выбрать команду Сервис–Поиск решения;
2) нажать кнопку  , затем кнопку
, затем кнопку  ;
;
3) выделить диапазон ячеек, содержащий параметры модели и нажать кнопку  ;
;
4) в диалоговом окне Параметры поиска решения нажать кнопку  ;
;
чтобы запустить процесс поиска, необходимо нажать кнопку  или кнопку
или кнопку  , чтобы запустить этот процесс позднее с выбранными параметрами.
, чтобы запустить этот процесс позднее с выбранными параметрами.
Содержание работы
2.1 Запустить программу MS Excel.
2.2 Создать файл аналогичный примеру 1 (Модель сбыта) со всеми расчетными формулами.
2.3 Рассмотреть все варианты нахождения оптимального решения в примере 1, установив надстройку Поиск решения.
2.4 Найти оптимальное решение с помощью надстройки Поиск решения в заданиях для самостоятельного решения из Приложения А. Вариант задания выбирается по указанию преподавателя.
2.5 Создать один из видов отчетов по результатам поиска решения.
2.6 Ответить на контрольные вопросы.
2.7 Составить отчет о проделанной работе, который должен содержать название работы, постановку задачи исследования, сведения о последовательности выполнения заданий с результатами и ответы на контрольные вопросы, указанные преподавателем.
3 Методика выполнения работы. Нахождение оптимального решения с помощью надстройки Поиск решения на примере задачи Модель сбыта
Работу с надстройкой Поиск решения рассмотрим на примере Модель сбыта (рисунок 1.11).
Эта типичная модель сбыта, отражающая ожидаемое увеличение числа продаж от заданной величины (обусловленной, например, затратами на персонал) при увеличении затрат на рекламу и уменьшении прибыли.
Пример 1. Модель сбыта
Добавление ограничения
Итак, бюджет покрывает расходы на рекламу и обеспечивает получение прибыли, однако, наблюдается тенденция к уменьшению эффективности вложений.
Поскольку нет гарантии, что данная модель зависимости прибыли от затрат на рекламу будет работать в следующем году (учитывая существенное увеличение затрат), целесообразно ввести ограничение расходов, связанных с рекламой. Предположим, расходы на рекламу за четыре квартала не должны превышать 40000 р. Добавим в рассмотренную задачу соответствующее ограничение.
Для этого необходимо:
1) Выбрать команду Сервис-Поиск решения и нажать кнопку  .
.
2) В диалоговом окне Добавление ограничения (рисунок 1.14) нужно задать ссылку на ячейку ограничения F11 (общие расходы на рекламу).
Содержимое этой ячейки не должно превышать 40000 р. Установленное по умолчанию отношение <= оставить без изменения. В поле, расположенном справа, нужно ввести число 40000 и нажать кнопку  .
.
3) Запустить процесс поиска решения кнопкой  .
.
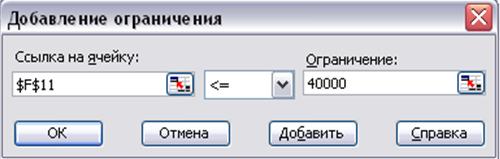
Рисунок 1.14 Диалоговое окно Добавление ограничения
В соответствии с найденным решением на рекламу будет выделено 5117р. в 3 квартале и 15263р. - в 4. Прибыль увеличится с 69662р. до 71447р. (рисунок 1.15).
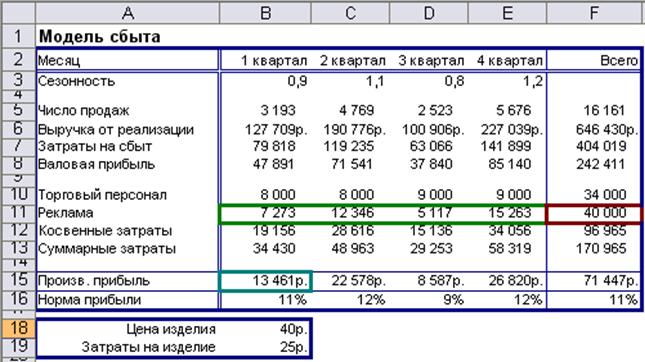
Рисунок 1.15 Нахождение наибольшей прибыли без увеличения бюджета на рекламу в задачеМодель сбыта
Изменение ограничения
Поиск решения позволяет экспериментировать с различными параметрами задачи, для определения наилучшего варианта решения. Например, изменив ограничения, можно оценить изменение результата. Попробуем на листе примера изменить ограничение на рекламный бюджет с 40000р. до 50000р. и посмотреть, как изменится при этом общая прибыль.
Для этого необходимо:
1) Выбрать команду Сервис - Поиск решения и нажать кнопку  , предварительно выделив предыдущее ограничение $F$11<=40000.
, предварительно выделив предыдущее ограничение $F$11<=40000.
2) В диалоговом окне Изменение ограничения (рисунок 1.16) нужно изменить поле значения 40000 на 50000 и нажать кнопку  .
.
3) Запустить процесс поиска решения кнопкой  .
.
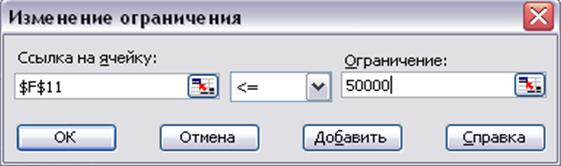
Рисунок 1.16 Диалоговое окно Изменение ограничения
Найденное решение соответствует прибыли 74817р., что на 3370 р. больше прежнего значения 71447 р. (рисунок 1.17).
Для большинства предприятий увеличение капиталовложений на 10000 р., приносящее 3370 р. (т.е. 33,7 % возврат вложений) является оправданным.
Прибыль при таком решении будет на 4889 р. меньше, по сравнению с задачей без ограничений, однако при этом требуется и на 39706 р. капиталовложений меньше.
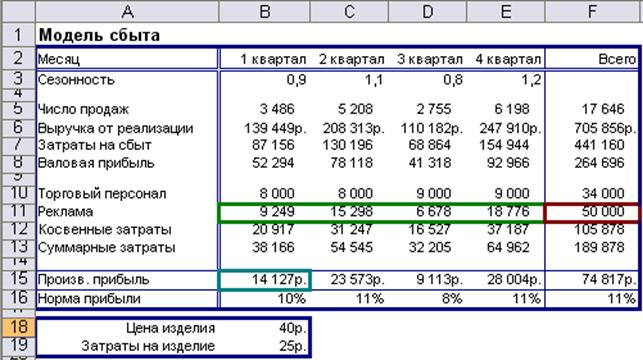
Рисунок 1.17 Нахождение наибольшей прибыли без увеличения бюджета на рекламу (с измененным ограничением) в задачеМодель сбыта
Вопросы для самоконтроля знаний
4.1 Что такое оптимизационная задача?
4.2 Для чего предназначена надстройка Поиск решения?
4.3 Как установить надстройку Поиск решения?
4.4 Какие бывают виды ограничений?
4.5 Перечислите переключатели группы Равной диалогового окна Поиск решения?
4.6 Как сохранить найденное решение?
4.7 Как добавить ограничения?
4.8 Для чего предназначена кнопка параметры?
4.9 Как восстановить исходные значения?
4.10 Как сохранить сценарий?
4.11 Как создать отчет по результатам поиска решения?
4.12 Какие бывают типы отчетов?
4.13 Как загрузить параметры модели?
4.14 Как сохранить параметры модели?
Лабораторная работа №2
«Решение задач линейного программирования методом оптимизации с помощью надстройки Поиск решения»
Цель работы:Овладеть приемами работы с надстройкой Поиск решения при решении задач линейного программирования. Научиться:
ü находить оптимальное решение задачи с помощью надстройки Поиск решения при решении задач линейной оптимизации;
ü создавать отчеты по результатам поиска решения;
ü сохранять параметры модели.
Общие сведения
Линейная оптимизация
Линейное программирование – это раздел математического программирования, посвященный нахождению экстремума линейных функций нескольких переменных при дополнительных линейных ограничениях, которые налагаются на переменные. Методы, с помощью которых решаются задачи, подразделяются на универсальные (например, симплексный метод) и специальные. С помощью универсальных методов решаются любые задачи линейного программирования. Особенностью задач линейного программирования является то, что экстремум целевой функции достигается на границе области допустимых решений.
Большую часть задач оптимизации представляют собой задачи линейного программирования, т. е. такие, у которых критерий оптимизации и ограничения – линейные функции. В этом случае для решения задачи следует установить флажок Линейная модельв окне Параметры поиска решения.Это обеспечит применение симплекс-метода. В противном случае даже для решения линейной задачи будут использоваться более общие (т.е. более медленные) методы.
Поиск решения может работать также и с нелинейными зависимостями и ограничениями. Это, как правило, задачи нелинейного программирования или, например, решение системы нелинейных уравнений. Для успешной работы средства Поиск решенияследует стремиться к тому, чтобы зависимости были гладкими или, по крайней мере, непрерывными.
Решая задачи с нелинейными зависимостями, следует:
ü ввести предварительно предположительные значения искомых переменных (иногда легко получить графическое представление решения и сделать приблизительные выводы о решении);
ü в окне Параметры поиска решенияснять (если установлен) флажок Линейная модель.
Содержание работы
2.1 Запустить программу MS Excel.
2.2 Создать файл аналогичный примеру 1 (Планирование производства материалов).
2.3 Рассмотреть все варианты нахождения оптимального решения в примере 1, установив надстройку Поиск решения.
2.4 Найти оптимальное решение с помощью надстройки Поиск решения задач линейного программирования в заданиях для самостоятельного решения из Приложения Б. Вариант задания выбирается по указанию преподавателя.
2.5 Создать один из видов отчетов по результатам поиска решения.
2.6 Ответить на контрольные вопросы.
2.7 Составить отчет о проделанной работе, который должен содержать название работы, постановку задачи исследования, сведения о последовательности выполнения заданий с результатами и ответы на контрольные вопросы, указанные преподавателем.
3 Методика выполнения работы. Нахождение оптимального решения линейной задачи с помощью надстройки Поиск решения на примере задачи Планирование производства материалов
Работу с надстройкой Поиск решения рассмотрим на примере задачи Планирование производства материалов.
Пример 1. Планирование производства материалов
Фирма выпускает два типа строительных материалов: А и В. Продукция обоих видов поступает в продажу. Для производства материалов используются два исходных продукта: I и II. Максимально возможные суточные запасы этих продуктов составляют 7 и 9 тонн соответственно. Расходы продуктов I и II на 1 тонну соответствующих материалов приведены в таблице 2.1. Изучение рынка сбыта показало, что суточный спрос на материал В никогда не превышает спроса на материал А более чем на 1 тонну. Кроме того, спрос на материал А никогда не превышает 3 тонны в сутки. Оптовые цены одной тонны материалов равны: 4000 у.е. для В и 3000 у. е. для А. Какое количество материала каждого вида должна производить фабрика, чтобы доход от реализации был максимальным?
Таблица 2.1 Расход продуктов
| Исходный продукт | Расход исходных продуктов, т (на одну тонну материалов) | Максимально возможный запас, т | |
| материал А | материал В | ||
| I | |||
| II |
Планирование производства материалов
Переменные задачи Х1 и Х2 находятся, соответственно, в ячейках СЗ и С4. Целевая функция находится в ячейке С6 и содержит формулу: =4000*С4+3000*С3. Ограничения на задачу учтены в ячейках C8:D11.
ü ввод данных в окно Поиск решения необходимо произвести в соответствии с рисунком 2.2.
Воспользовавшись командой Сервис - Поиск решения,нужно ввести необходимые данные для рассматриваемой задачи (установка данных в окне Поиск решенияприведена на рисунке 2.2).
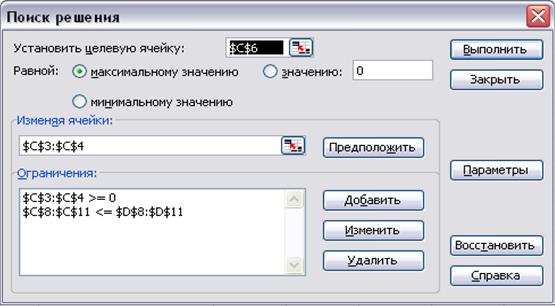
Рисунок 2.2 Установка необходимых параметров задачи планирования материалов в окне Поиск решения
ü полученное оптимальное решение представлено на рисунке 2.3.
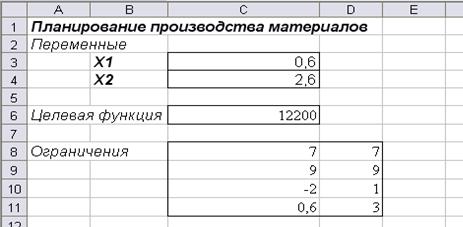
Рисунок 2.3Результат расчета с помощьюнадстройки Поиск решения
Вопросы для самоконтроля знаний
4.1 Что такое линейное программирование?
4.2 Что такое задача нелинейного программирования?
4.3 Какую опцию нужно установить в окне Параметры поиска решения для решения задач по линейному программированию?
4.4 Назовите виды задач линейного программирования.
Лабораторная работа №3
«Решение транспортных задач методом оптимизации с помощью надстройки Поиск решения»
Цель работы:Овладеть приемами работы с надстройкой Поиск решения при решении транспортных задач. Научиться:
ü находить оптимальное решение задачи с помощью надстройки Поиск решения при решении транспортных задач;
ü создавать отчеты по результатам поиска решения;
ü сохранять параметры модели.
Общие сведения
Транспортная задача
В общем виде транспортную задачу можно сформулировать следующим образом: в m пунктах отправления А1,...,Аm находится однородный груз, количество которого равно соответственно а1,...,аm единиц. Данный груз необходимо доставить потребителям B1,...,Вn, спрос которых - b1,...,bn. Стоимость перевозки единицы груза из i-го (i = 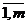 ) пункта отправления в j-й (j =
) пункта отправления в j-й (j = 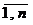 ) пункт назначения равна Сi,j. Необходимо составить план перевозок, который полностью удовлетворяет спрос потребителей в грузе, и при этом суммарные транспортные издержки минимальны.
) пункт назначения равна Сi,j. Необходимо составить план перевозок, который полностью удовлетворяет спрос потребителей в грузе, и при этом суммарные транспортные издержки минимальны.
Математически транспортную задачу можно записать так:
F = 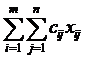
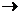 min, (1)
min, (1)
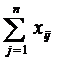 = ai,, i =
= ai,, i = 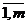 ,
, 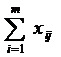 = bj,, j =
= bj,, j = 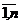 , (2)
, (2)
xij >= 0, i = 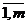 , j =
, j = 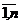 . (3)
. (3)
Таким образом, дана система ограничений (2) при условии (3) и линейная функция (1). Требуется среди множества решений системы (2) найти такое неотрицательное решение, которое доставляет минимум линейной функции (1).
Модель транспортной задачи называют закрытой (сбалансированной), если суммарный объем груза, имеющегося у поставщиков, равен суммарному спросу потребителей, т. в. выполняется равенство:
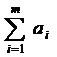 =
= 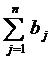 .
.
Если для транспортной задачи выполняется одно из условий:
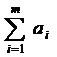 >
> 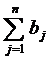 ,
, 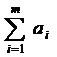 <
< 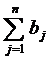 ,
,
то модель задачи называют открытой (несбалансированной).
Для разрешимости транспортную задачу с открытой моделью следует преобразовать в закрытую.
ü Так, если выполняется условие 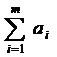 >
> 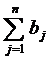 , то необходимо ввести фиктивный (n+1)-й пункт назначения Вn+1, т. е. в матрицу задачи вводится дополнительный столбец. Спрос фиктивного потребителя принимается равным bn+1 =
, то необходимо ввести фиктивный (n+1)-й пункт назначения Вn+1, т. е. в матрицу задачи вводится дополнительный столбец. Спрос фиктивного потребителя принимается равным bn+1 = 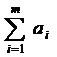 -
- 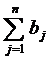 . Стоимость перевозок продукции полагается одинаковой, чаще всего равной нулю (если не задана стоимость складирования продукции), т. е. сi,n+1 = 0, i =
. Стоимость перевозок продукции полагается одинаковой, чаще всего равной нулю (если не задана стоимость складирования продукции), т. е. сi,n+1 = 0, i = 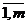 .
.
ü Если выполняется условие 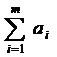 <
< 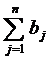 , то необходимо ввести фиктивного (m+1)-го поставщика Am+1, т. е. в матрицу задачи вводится дополнительная строка. Запас груза данного поставщика принимается равным am+1 =
, то необходимо ввести фиктивного (m+1)-го поставщика Am+1, т. е. в матрицу задачи вводится дополнительная строка. Запас груза данного поставщика принимается равным am+1 = 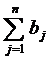 -
- 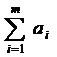 . Стоимость перевозок продукции полагается одинаковой, чаще всего равной нулю (если не задана стоимость штрафов за недопоставку продукции), т. е. cm+1,j = 0, j =
. Стоимость перевозок продукции полагается одинаковой, чаще всего равной нулю (если не задана стоимость штрафов за недопоставку продукции), т. е. cm+1,j = 0, j =
