Течение вязкой несжимаемой жидкости

На течение реальной жидкости существенное влияние оказывает вязкость. Еще в начале XX века Джон фон Нейманн отмечал, что красивые математические задачи, решенные в рамках приближения идеальной жидкости, ничего общего с движениями реальных жидкостей не имеют. Он называл теоретиков, которые занимались подобными расчетами, людьми, изучающими “сухую воду”. Первые опыты, показывающие влияние сил вязкости на сопротивление при малых скоростях, принадлежат Кулону и Дюбуа. Основы учения о движении вязкой жидкости были заложены в 1821 г. французским ученым Навье и получили завершение в 1845 г. в работах Стокса.

В этом разделе мы выведем уравнения, описывающие течение “мокрой воды”. Для этого запишем закон сохранения импульса (3.7) в случае отсутствия внешних сил:

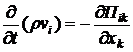, (8.1)

где 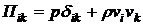- тензор плотности потока импульса. Действие вязких сил можно учесть, вводя в 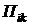дополнительное слагаемое 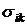, называемое тензором вязких напряжений и характеризующее величину 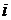-ой компоненты вязкой силы, действующей на единичную площадку, ориентированную перпендикулярно 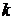-ой оси. Тогда тензор плотности потока импульса примет вид:

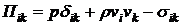. (8.2)

Поскольку трение может возникнуть только в случае, когда различные участки жидкости движутся с разными скоростями, 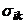должен зависеть от градиентов скорости:

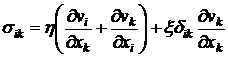, (8.3)

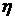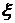где и - коэффициенты вязкости. Для несжимаемой жидкости 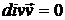(см. задачу 1.11), и второе слагаемое в (8.3) обращается в нуль.

Уравнение движения вязкой жидкости, называемое уравнением Навье-Стокса, можно получить при подстановке выражения для тензора плотности потока импульса в виде (8.2) с учетом (8.3) в уравнение (8.1) и полагая, что динамический коэффициент вязкости 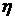не зависит от координат. Для несжимаемой жидкости имеем:

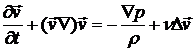, (8.4)

где 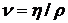- кинематическая вязкость жидкости.

Частицы вязкой жидкости прилипают к поверхности обтекаемого тела, поэтому их скорость на границе равна нулю (это так называемое граничное условие “прилипания”). Тогда из (8.1)-(8.2) несложно вычислить силу, действующую на твердое тело со стороны установившегося (стационарного) потока вязкой жидкости:

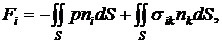
где 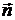- внешняя нормаль к поверхности тела 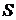. Здесь первое слагаемое представляет собой результирующую сил давления жидкости на тело, а второе определяет вязкую силу. Следовательно, вязкая сила, действующая на единицу поверхности тела, равна

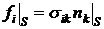. (8.5)

Примеры решения задач

1. Определить движение вязкой несжимаемой жидкости между двумя бесконечными пластинами, находящимися на расстоянии друг от друга (течение Куэтта). Верхняя пластина движется со скоростью 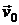, нижняя – неподвижна. Найти плотность силы 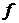, действующей на единицу площади нижней пластины со стороны жидкости.

Решение: Выберем систему координат: пусть ось 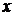совпадает с направлением скорости 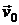, а ось 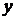направлена перпендикулярно пластинам, начало координат возьмем на нижней неподвижной пластине.

В силу симметрии задачи скорость и давление в произвольной точке жидкости могут зависеть только от координаты : , .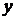

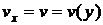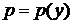Спроецируем уравнение Навье - Стокса (8.4) на ос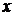и и 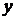с учетом стационарности движения ( ):

,

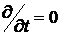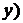
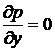следовательно, ;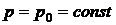

,

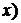
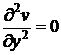следовательно, .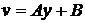

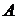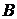Постоянные и определяются из граничных условий “прилипания”:

1) ,

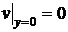2) .

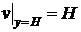Отсюда легко получаем, что 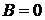, 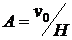. Таким образом, скорость движения жидкости в течении Куэтта равна

.

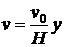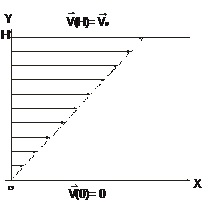
Теперь полученный нами линейный профиль скорости необходимо схематически изобразить на рисунке линиями со стрелочками, показывающими направление скорости (см. рисунок).

Сила 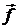, действующая на единицу площади нижней пластины со стороны жидкости, имеет две компоненты. Нормальная составляющая определяется силой давления:

.

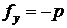Тангенциальная компонента - это вязкая сила, которая, согласно (8.5), равна

.

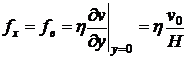Замечание. В гидродинамике важным является понятие о коэффициенте сопротивления, характеризующем отношение вязкой силы к так называемому скоростному напору :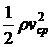

,

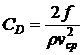где 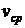- средняя (или некоторая характерная) скорость потока: 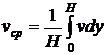. В случае течения Куэтта 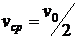, и коэффициент сопротивления равен

.

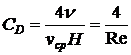Здесь 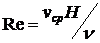- число Рейнольдса.

Задачи для самостоятельного решения

8.1. Вывести уравнение движения несжимаемой жидкости с учетом вязких сил (уравнение Навье - Стокса).

8.2. Спроецировать уравнение Навье - Стокса (8.4) в декартовой, цилиндрической и сферической системах координат.

8.3. Показать, что для вязкой несжимаемой жидкости, в случае потенциальности внешних сил, вектор угловой скорости частиц 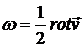удовлетворяет уравнению:

.

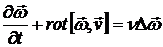8.4. Исследовать стационарное течение вязкой несжимаемой жидкости между двумя неподвижными бесконечными пластинами, находящимися на расстоянии друг от 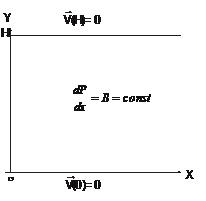друга, поддерживаемое продольным градиентом давления 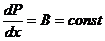, созданным внешними силами (течение Пуазейля). Определить профиль скорости 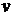, плотность вязкой силы 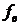, действующей на единицу площади каждой пластины со стороны протекающей жидкости, среднюю скорость потока 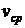и коэффициент сопротивления .

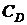Ответ: ; ; ; .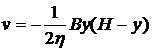

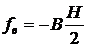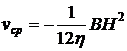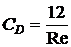8.5. 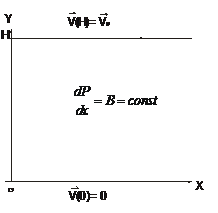Определить установившееся движение вязкой несжимаемой жидкости между двумя бесконечными пластинами, находящимися на расстоянии друг от друга. Верхняя пластина движется со скоростью 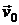, нижняя – неподвижна. Задан продольный градиент давления 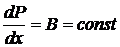, созданный внешними силами. Исследовать (и нарисовать) профиль течения при различных значениях 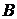и определить силы вязкости, действующие на единицу площади каждой пластины со стороны протекающей жидкости.

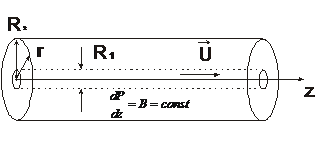
8.6. 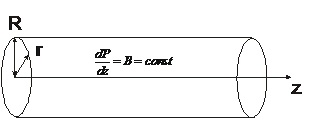Определить установившееся движение вязкой несжимаемой жидкости в круговой трубе радиуса 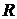, которое поддерживается продольным градиентом давления 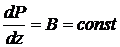, созданным внешними силами. Исследовать профиль скорости, найти плотность вязкой силы 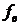, действующей на единицу площади трубы стороны протекающей жидкости, среднюю скорость потока 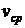и коэффициент сопротивления 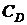. Определить объем жидкости 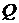, протекающей через поперечное сечение трубы в единицу времени (расход жидкости).

Ответ: ; ; ; ; .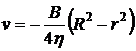

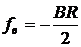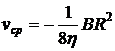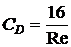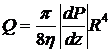8.7. Цилиндр радиуса 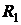движется со скоростью 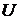внутри коаксиального с ним цилиндра радиуса 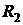параллельно своей оси. Определить движение жидкости, заполняющей пространство между цилиндрами. Найти плотности вязких сил 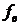, действующих на единицу площади каждого из цилиндров со стороны протекающей жидкости.

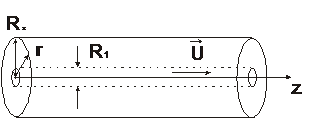
Ответ: .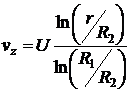

8.8. Рассчитать профиль скорости для течения Пуазейля между двумя коаксиальными цилиндрами радиусов 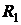и 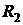, если задан продольный градиент давления 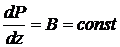, созданный внешними силами. Найти расход жидкости .

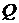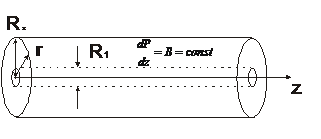
Ответ: ;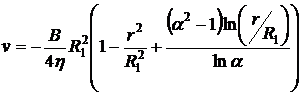

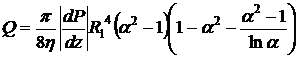, где .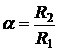

8.9. Рассчитать профиль скорости для течения Пуазейля между двумя коаксиальными цилиндрами радиусов 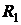и 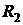, если задан продольный градиент давления 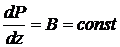, созданный внешними силами. Внешний цилиндр покоится, а внутренний движется со скоростью 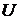. Найти плотности вязких сил 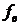, действующих на единицу длины каждого из цилиндров со стороны протекающей жидкости. Определить, при каком значении 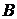эти силы равны нулю.

8.10. Определить установившееся движение вязкой несжимаемой жидкости по трубе, если ее поперечное сечение – эллипс: 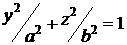; 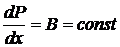. Найти расход жидкости .

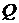Ответ: ;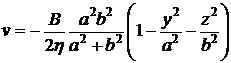

.

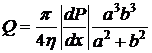8.11. Для стационарного движения вязкой несжимаемой жидкости в длинной горизонтальной цилиндрической трубе произвольного поперечного сечения заданной площади под действием постоянного продольного перепада давления 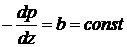(течение Пуазейля), используя теорию размерности, получить формулы для объемного расхода жидкости 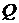и максимальной по сечению скорости .

Ответ: 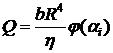, , 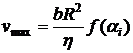где 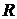- характерный размер поперечного сечения трубы, 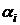- безразмерные параметры, задающие его форму.

8.12. 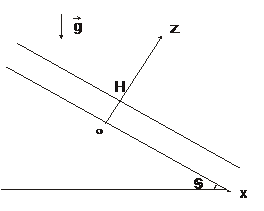Слой вязкой несжимаемой жидкости толщины ограничен сверху свободной поверхностью, а снизу – неподвижной плоскостью, наклоненной под углом 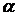к горизонту. Определить движение жидкости, возникающее под влиянием силы тяжести: найти давление 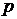, скорость 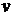и количество жидкости 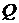, протекающее в единицу времени через поперечное сечение слоя (на единицу длины по ).

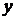Указания: Уравнение Навье - Стокса (8.4) с учетом силы тяжести принимает вид:

.

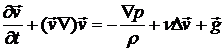На свободной поверхности при 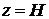должны выполняться граничные условия: , .

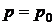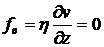Ответ: ;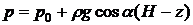

;

.

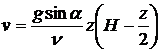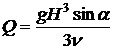8.13. 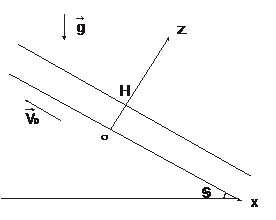Слой вязкой несжимаемой жидкости толщины ограничен сверху свободной поверхностью, а снизу – плоскостью, наклоненной под углом 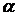к горизонту и двигающейся со скоростью 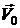. Определить движение жидкости, возникающее под влиянием силы тяжести: найти давление 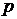, скорость 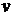и объемный расход жидкости 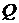, (на единицу длины по 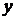). При каком значении 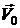объемный расход жидкости 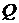=0?

8.14. Рассчитать с учетом силы тяжести течение Пуазейля в круглой трубе, образующая которой наклонена к горизонту под углом .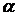

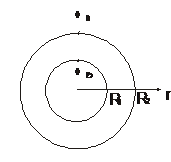
8.15. Найти профили скорости 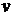и давления 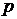в случае течения Куэтта между двумя соосными цилиндрами радиусов 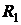и 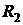, вращающихся вокруг общей оси с угловыми скоростям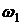и и 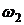соответственно.

Ответ: ;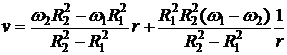

,

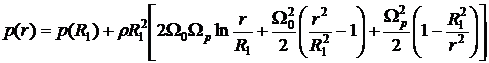где , .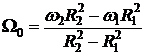

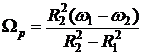8.16. Используя решение задачи 8.15, определить силу трения 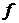, действующую на единицу поверхности внутреннего цилиндра и момент вязких сил 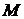, действующий на единицу длины цилиндра.

Ответ: ;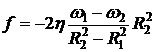

.

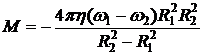8.17. Скорость течения в центре трубы диаметра 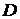и длины 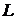равна 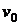. Определить разность давлений на концах трубы 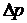и объемный расход жидкости 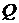, если известна вязкость жидкости .

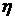Ответ: ;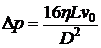

.

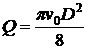8.18. Чему должна равняться разность давлений на концах нефтепровода длины 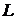и радиуса 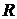, чтобы нефть плотностью 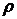и вязкостью 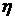поступала в количестве ?

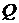Ответ: .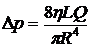

8.19. 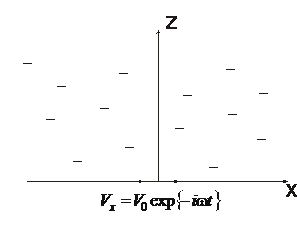Бесконечная пластина, расположенная в плоскости 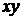и ограничивающая полупространство 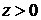, заполненное однородной несжимаемой вязкой жидкостью, совершает гармонические колебания:

; .

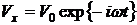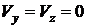Получить выражение для скорости частиц жидкости 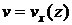, определить толщину скин-слоя 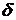и плотность вязкой силы, действующей на пластину, .

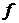Ответ: ;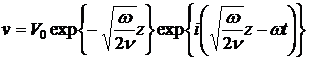

;

.

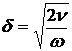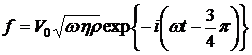8.20. 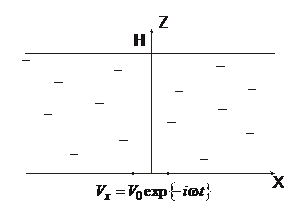Получить выражение для вязких волн между параллельными стенками, отстоящими друг от друга на расстояние , если одна из стенок покоится, а другая колеблется в своей плоскости по закону

; .

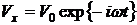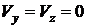Найти амплитуду вязкой силы 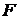, действующую на единицу площади неподвижной стенки.

Ответ: ,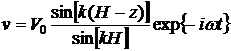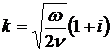

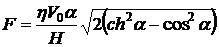где ;

, где .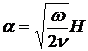

8.21. Слой вязкой несжимаемой жидкости толщины соприкасается с неограниченной плоской поверхностью, совершающей в своей плоскости гармонические колебания с частотой 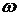. Определить скорость движения жидкости при условии, что верхняя поверхность слоя является свободной.

Указание: корректно записать граничное условие на свободной поверхности (см. задачу 8.12).

8.22. Определить движение жидкости между 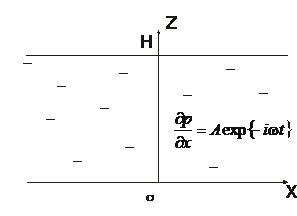двумя параллельными плоскостями, находящимися на расстоянии друг от друга, при наличии продольного градиента давления, изменяющегося со временем по гармоническому закону:

.

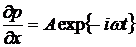Ответ: ,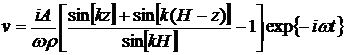

где .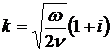

8.23. Получить выражение для силы сопротивления, которую испытывает шар радиуса 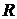при движении со скоростью 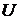в вязкой несжимаемой жидкости в случае малых чисел Рейнольдса (формулу Стокса).

8.24. Шарик плотности 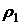падает в вязкой несжимаемой жидкости с плотностью 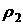и вязкостью 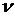. Определить установившуюся скорость движения 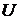, если радиус шарика равен 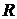. Оценить число Рейнольдса .

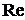Ответ: ; .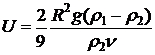

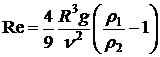8.25. Оценить, для каких размеров песчинки, падающей в воде, можно использовать формулу Стокса.

Указание: Воспользоваться решением задачи 8.25, положив при этом 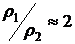, 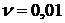см²/c, .

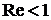8.26. Капля воды падает с установившейся скоростью в воздухе. Оценить, для каких размеров капель можно использовать формулу Стокса для вычисления силы сопротивления.

Указание: Воспользоваться решением задачи 8.25, положив при этом 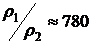, 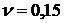см²/c, .

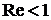8.27. Образовавшийся в стакане жидкости пузырек радиуса 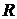всплывает к поверхности со скоростью 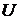. Оценить вязкость жидкости.

Ответ: .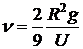

Контрольные вопросы

1. Уравнение движения вязкой несжимаемой жидкости. Его представление в векторной форме и в проекциях в декартовой системе координат.

2. Тензор вязких напряжений. Его физический смысл и представление в декартовой системе координат.

3. Колебательные движения вязкой несжимаемой жидкости. Вязкие волны. Понятие скин - слоя

4. Пограничный слой.