Плоское потенциальное течение идеальной несжимаемой жидкости. Функция тока. Комплексный потенциал

Полнее всего теория потенциального движения идеальной несжимаемой жидкости разработана в случае плоского потенциального течения (когда от одной координаты, например, от 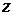, ничего не зависит, и 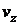=0).

Введем новую функцию 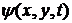- функцию тока – так, чтобы уравнение неразрывности

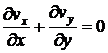
удовлетворялось автоматически. Для этого положим:

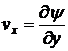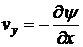, . (5.1)

Термин «функция тока» обусловлен тем, что линиями тока течения являются линии .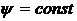

В случае потенциального течения, когда 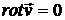, функция тока удовлетворяет уравнению Лапласа:

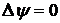. (5.2)

Введем для плоского течения функцию потенциала скорости 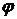: 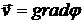. Тогда

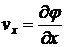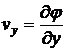, . (5.3)

Несложно показать, что линии тока ( 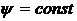) ортогональны изопотенциальным линиям ( ).

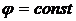Соотношения (5.1) и (5.2) с математической точки зрения совпадают с условиями Коши - Римана, выражающими собой тот факт, что функция

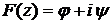(5.4)

является аналитической функцией комплексного аргумента 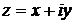, т.е. обладает свойством дифференцируемости. Функцию 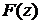называют комплексным потенциалом, а функцию 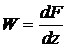- комплексной скоростью. Следовательно, любой аналитической функции комплексной переменной можно поставить в соответствие некое плоское потенциальное течение идеальной несжимаемой жидкости. Впервые подобный подход к решению данного класса задач был предложен Д’Аламбером и Эйлером в середине XVIII века, а современное изложение дано в 1876 г. Кирхгофом.

Примеры решения задач

1. Изучить движение жидкости, описываемое комплексным потенциалом

,

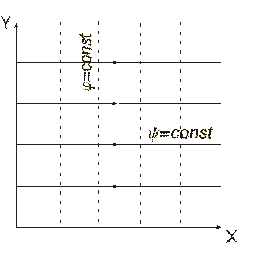
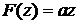где 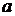- вещественная постоянная. Найти линии тока и эквипотенциальные линии.

Решение: Поскольку 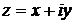, то .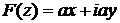

С другой стороны, комплексный потенциал выражается через потенциал скорости 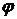и функцию тока 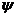формулой (5.4).

Следовательно, в данной задаче

,

.

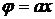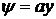Компоненты вектора скорости можно найти либо через функцию потенциала, используя выражения (5.3), либо через функцию тока, используя соотношения (5.1).

Несложно вычислить, что

,

.

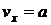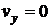Для полного решения задачи следует нарисовать на плоскости 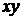линии тока, указывая стрелочками направление скорости течения жидкости, и линии равного потенциала, обозначаемые, как правило, пунктиром (см. рисунок). Очевидно, что данный комплексный потенциал определяет “однородный поступательный поток” жидкости.

Задачи для самостоятельного решения

5.1. Доказать, что при плоском потенциальном движении несжимаемой жидкости функция тока удовлетворяет уравнению Лапласа.

5.2. Показать, что линии 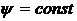являются линиями тока.

Указание: учесть, что для линии тока 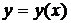справедливо соотношение .

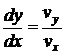5.3. Доказать, что линии тока ( 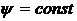) и эквипотенциальные линии ( 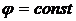) образуют два семейства ортогональных линий.

5.4. Найти выражение для комплексной скорости 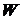через компоненты вектора скорости , .

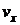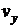5.5. Доказать, что при плоском потенциальном течении несжимаемой жидкости имеет место соотношение

,

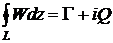где 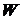- комплексная скорость, 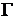и 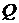- соответственно циркуляция скорости и расход жидкости по любому замкнутому контуру 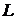, принадлежащему области, занятой жидкостью.

5.6. Выразить через функцию тока 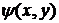расход жидкости Q через криволинейную дугу, соединяющую точки с координатам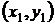и и .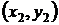

Ответ: .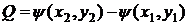

5.7. Выразить через потенциал скорости 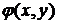циркуляцию скорости Г по кривой, соединяющей точки с координатам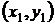и и .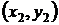

Ответ: .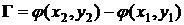

5.8. Изучить движение жидкости, определяемое комплексным потенциалом

,

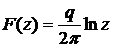где 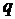- вещественная постоянная. Найти компоненты скорости 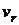, 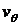( 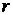, 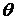- полярные координаты), циркуляцию скорости и расход жидкости через окружность с центром в начале координат. Найти линии тока и эквипотенциальные линии.

5.9. Изучить движение жидкости, определяемое комплексным потенциалом

,

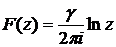где 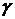- вещественная постоянная. Найти компоненты скорости 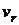, 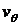( 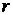, 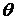- полярные координаты), циркуляцию скорости и расход жидкости через окружность с центром в начале координат. Найти линии тока и эквипотенциальные линии.

5.10. Показать, что для плоских течений несжимаемой жидкости вектор скорости 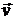связан с функцией тока 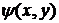следующим соотношением:

,

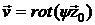где 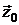- единичный вектор нормали к плоскости .

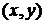5.11. Изучить движение жидкости, определяемое комплексным потенциалом

,

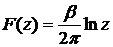где 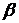- комплексное число. Найти компоненты скорости 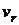, 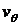( 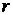, 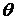- полярные координаты), циркуляцию скорости и расход жидкости через окружность с центром в начале координат. Найти линии тока и эквипотенциальные линии.

5.12. Изучить движение жидкости, определяемое комплексным потенциалом

,

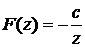где 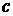- вещественная постоянная. Найти линии тока, эквипотенциальные линии и скорость течения жидкости.

5.13. Изучить движение жидкости, определяемое комплексным потенциалом

,

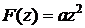где 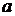- вещественная постоянная. Найти линии тока и эквипотенциальные линии.

5.14. Рассмотреть движение жидкости, определяемое комплексным потенциалом

,

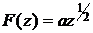где 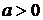, в области, получающейся, если вдоль положительной оси 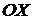поставить стенку. Показать, что линиями тока служат параболы.

5.15. Показать, что комплексный потенциал

,

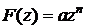где 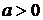, , 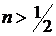соответствует обтеканию угла с раствором 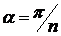. Найти скорость течения в точке .

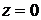5.16. Провести полный анализ течения, соответствующего потенциальному обтеканию кругового цилиндра с циркуляцией, которое имеет комплексный потенциал

,

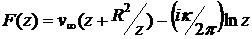где 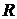- радиус цилиндра, 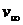- скорость натекающего потока на бесконечности, 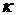- вещественная постоянная (для определенности 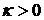). Найти компоненты скорости 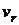, 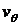. Определить величину скорости 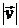и давление 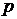на поверхности цилиндра.

5.17. Качественно представить картину линий тока течения, которому соответствует комплексный потенциал

.

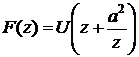Ответ: Течение является суперпозицией поступательного потока и течения от диполя, помещенного в точке .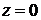

Линии тока:

, .

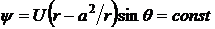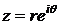Уравнение обтекаемого контура .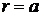

5.18. Качественно представить картину линий тока течения, которому соответствует комплексный потенциал

.

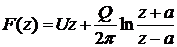Ответ: Течение является суперпозицией поступательного потока и течений, создаваемых источником, расположенным в точке 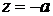, и стоком в точке .

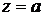Линии тока:

.

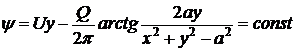Обтекаемый контур 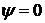представляет собой овал, проходящий через точки .

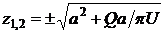Пр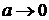и и 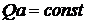получим функцию тока

,

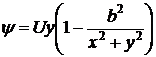соответствующую обтеканию кругового цилиндра. Здесь .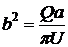

5.19. Проверить, что комплексный потенциал обтекания кругового цилиндра, заданного уравнением 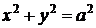, имеет вид:

,

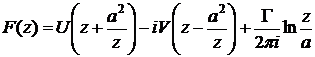где 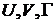— действительные постоянные. Какой физический смысл имеют эти постоянные?

5.20. Показать, что поле скорости с потенциалом

, ,

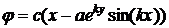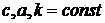определяет течение несжимаемой жидкости. Найти функцию тока и комплексный потенциал этого течения. Какой физический смысл имеют параметры ?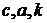

Ответ: , .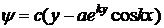

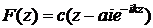Контрольные вопросы

1. Определение функции тока.

2. Определение комплексного потенциала.

3. Примеры плоских потенциальных течений.

4. Определение комплексной скорости.

Вихревое движение жидкости

Движение жидкости называется вихревым, если хотя бы в части объема, занимаемого жидкостью, 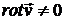. Рассмотрим основные свойства вихревого движения.

Выберем замкнутый контур, состоящий из фиксированных частиц, и, следовательно, перемещающийся вместе с ними (жидкий контур), и найдем полную производную от циркуляции скорости вдоль этого контура:

,

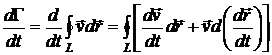поскольку контур меняется со временем. Из уравнения Эйлера (1.1) имеем

.

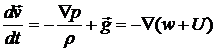Далее несложно показать, что 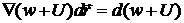, а 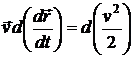. Таким образом,

,

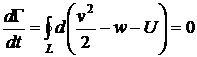так как интеграл по замкнутому контуру от полного дифференциала всегда равен нулю. Следовательно, циркуляция скорости по любому замкнутому контуру, перемещающемуся вместе с жидкостью, сохраняется:

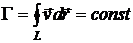. (6.1)

Поскольку эту теорему о циркуляции скорости впервые доказал в 1869 году Томсон (лорд Кельвин), она носит название теоремы Томсона.

Зная теорему Томсона, несложно доказать три другие теоремы о вихрях, которые исторически были получены несколько ранее (в 1858 году) Гельмгольцем и Лагранжем.

Первая теорема Гельмгольца (или теорема Лагранжа): элементы идеальной жидкости, лишенные вихрей в начальный момент времени, будут лишены их и в дальнейшем. Под «вихрем» или «вектором вихря» понимают векторную величину .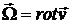

Введем понятие вихревой линии и вихревой трубки. Вихревой линией называют линию, касательная к которой в каждой точке коллинеарна вектору вихря. Из вихревых линий можно образовать вихревую трубку. Для этого надо взять замкнутый контур и через каждую его точку провести вихревую линию.

Вторая теорема Гельмгольца: вихревая линия состоит все время из одних и тех же частиц, т.е. движется вместе с жидкостью.

Третья теорема Гельмгольца: поток вихря через поперечное сечение вихревой трубки 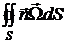остается постоянным вдоль данной вихревой трубки. Следовательно, вихревые линии всегда замкнуты или начинаются и кончаются на бесконечности, а также на стенках или на поверхности жидкости.

Примеры решения задач

1. 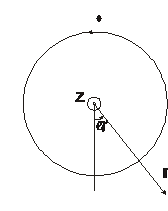Определить поле вихрей скорости в жидкости, вращающейся вокруг вертикальной оси 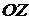с угловой скоростью .

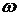Решение: Введем цилиндрическую систему координат 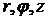. По условию задачи вектор скорости движения жидкости будет равен 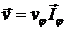. Поскольку угловая скорость 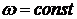, то

.

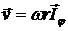Запишем вихрь скорости 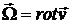в цилиндрической системе координат:

.

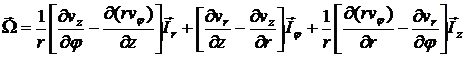Учтем, что 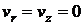, а 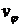зависит только от расстояния до оси вращения 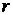. Тогда

.

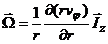Подставив 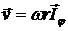, окончательно получаем:

.

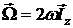2. Рассмотреть движение двух точечных вихрей, описываемых комплексными потенциалами:

,

.

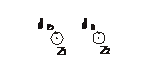
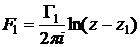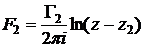Решение: Запишем общий комплексный потенциал в плоскости :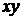

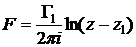
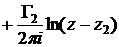
Здесь и далее примем обозначения , .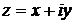

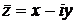Исследуем перемещение вихревых линий в пространстве.

.

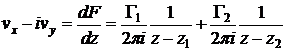Таким образом,

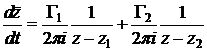
Учтем, что вихрь в точке 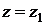перемещается только под действием поля скорости второго вихря в этой точке.

;

.

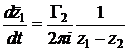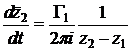Выделим в этих уравнениях действительные и мнимые части.

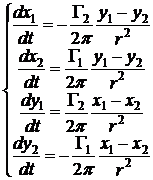
Здесь введено обозначение .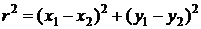

Умножим первое уравнение полученной системы на 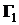, второе – на 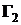и сложим, в результате получим:

,

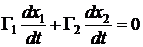следовательно,

.

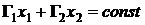Аналогично поступим с третьим и четвертым уравнениями системы.

,

.

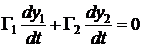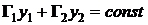Введем понятие центра инерции системы двух вихрей 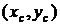следующим образом:

, .

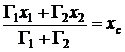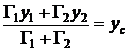Тогда можно сделать вывод, чтоцентр инерции системы двух вихрей 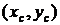при их движении остается неподвижным.

Кроме того, можно показать, что расстояние между вихрями остается постоянным. Для этого вернемся к полученной ранее системе уравнений. Вычитая из первого второе, а из третьего четвертое, имеем:

;

.

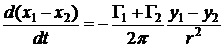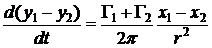Умножим первое из этих уравнений на 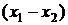, а второе – на 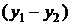и сложим полученные выражения, в результате получим:

.

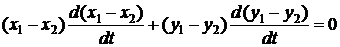Следовательно,

,

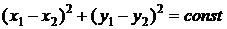то есть,

.

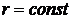Таким образом, при движении вихри вращаются вокруг центра инерции с сохранением расстояния между ними.

Задачи для самостоятельного решения

6.1. Доказать теорему Лагранжа: элементы идеальной жидкости, лишенные вихрей в начальный момент времени, будут лишены их и в дальнейшем.

6.2. Доказать вторую теорему Гельмгольца: вихревая линия состоит все время из одних и тех же частиц, т.е. движется вместе с жидкостью.

6.3. Доказать третью теорему Гельмгольца: поток вихря через поперечное сечение вихревой трубки остается постоянным вдоль данной вихревой трубки.

6.4. Сформулировать условия стационарности вихревых движений в идеальной жидкости.

Ответ: , , .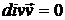

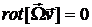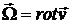6.5. Для однородной идеальной несжимаемой жидкости в поле потенциальных массовых сил из уравнения Эйлера вывести уравнение Гельмгольца:

,

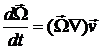где .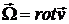

Указание: Записать уравнение Эйлера в форме Громэко - Лэмба и применить к нему операцию .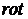

6.6. Определить поле вихрей скорости при сдвиге, принимая координатную плоскость 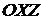за плоскость сдвига и считая, что скорости точек параллельны оси 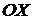так, что , , .

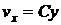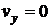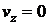Ответ: .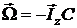

6.7. Доказать, что тангенциальный разрыв, когда один слой жидкости движется относительно другого с постоянной во всех точках скоростью 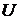, является примером стационарного вихревого движения.

6.8. 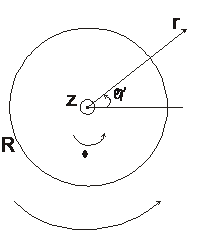Бесконечный жидкий круговой цилиндр радиуса 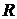вращается как целое с угловой частотой 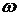. Считая движение жидкости вне цилиндра потенциальным, найти распределение скорости движения жидкости 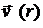в зависимости от расстояния от оси цилиндра.

Указание: использовать решение задачи 4.15.

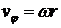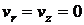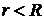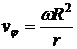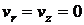Ответ: , при ;

, при .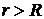

6.9. Бесконечный жидкий круговой цилиндр радиуса 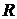вращается как целое с угловой частотой 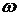. Считая движение жидкости вне цилиндра потенциальным, найти распределение давления 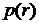в зависимости от расстояния от оси цилиндра, если на бесконечном удалении от оси цилиндра давление равно 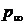. Плотность жидкости .

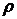Указание: воспользоваться решением задачи 6.8.

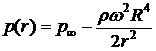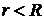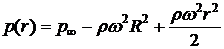Ответ: при ;

при .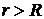

6.10. Скорости частиц жидкости пропорциональны расстояниям частиц от оси 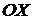и параллельны последней, так что 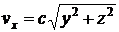, , 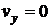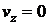. Определить поле вихрей.

Ответ: вихревые линии – окружности 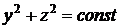, ; величина вихря везде одинакова .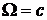

6.11. Рассмотреть, как будут двигаться точечные вихри в следующих ситуациях:

а) два вихря с одинаковыми по величине и направлению циркуляциями:

,

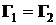рассмотреть случа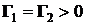и и 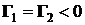, определить координаты центра инерции системы;

б) два вихря с одинаковыми по величине, но противоположными по направлению циркуляциями:

;

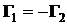в) вихрь вблизи твердой стенки;

г) два вихря с циркуляциями:

,

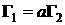рассмотреть случа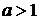и и .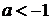

Ответ: а) вихри вращаются вокруг центра масс 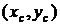, координаты которого определяются соотношениями , .

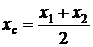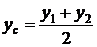б) вихри двигаются поступательно с постоянной скоростью перпендикулярно к прямой, соединяющей их.

Контрольные вопросы

1. Определение вихревого движения жидкости.

2. Примеры стационарных вихревых движений жидкости.

3. Циркуляция скорости. Теорема Томпсона о циркуляции.

4. Элементарные вихревые движения и их взаимодействия.