Потенциальное течение идеальной несжимаемой жидкости

Для описания движения идеальной несжимаемой жидкости запишем следующую систему уравнений:

,

.

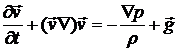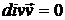Используя векторное тождество 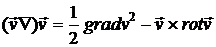в уравнении Эйлера, и применив к нему операцию 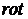, получим:

,

.

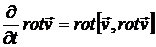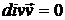Если движение жидкости потенциальное, то 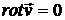, и система принимает вид:

,

.

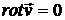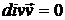Введем потенциал скорости 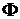: 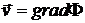. Тогда имеем

,

.

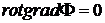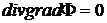Таким образом, решение задач о потенциальном течении идеальной несжимаемой жидкости сводится к решению одного скалярного уравнения

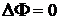(4.1)

с учетом граничных условий. Уравнение (4.1) носит название уравнения Лапласа, хотя еще Д’Аламбер и Эйлер в 1761 году занимались решением подобных уравнений для задач гидродинамики. При соприкосновении идеальной жидкости с твердым телом должно выполняться так называемое граничное условие «непроникания»:

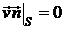или 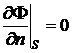, (4.2)

если тело покоится ( 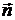- нормаль к поверхности раздела), и

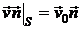или 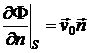, (4.3)

если тело движется со скоростью .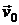

Примеры решения задач

1. 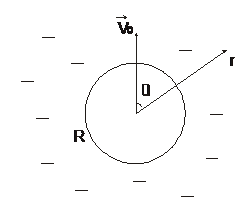Сфера радиуса 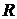движется с постоянной скоростью 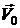в идеальной несжимаемой жидкости. Поставить краевую задачу для уравнения Лапласа. Получить выражение для потенциала 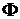и скорости частиц жидкости .

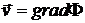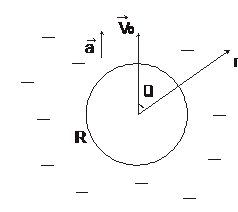
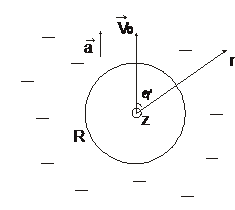
Решение: Воспользуемся сферической системой координат ( 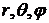), начало которой в данный момент времени совпадает с центром сферы, угол 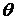будем отсчитывать от направления вектора скорости 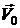. Запишем уравнение Лапласа:

.

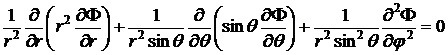В силу симметрии решение задачи не должно зависеть от азимутального угла 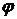, следовательно,

.

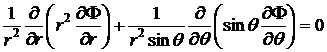Для корректного решения задачи необходимо поставить два граничных условия:

1. ,

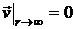2. .

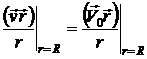Первое из них отражает тот факт, что частицы жидкости на бесконечности остаются в покое, второе – это граничное условие “непроникания” (4.3) – равенство нормальных к поверхности сферы составляющих скорости частиц жидкости и точек сферы.

Для функции потенциала скорости 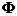граничные условия можно переписать следующим образом:

1. ,

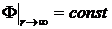2. .

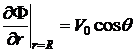Решение для функции потенциала будем искать в виде 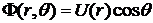, поскольку при этом автоматически выполняется граничное условие на поверхности шара. Подставляя данный вид 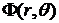в уравнение Лапласа, получаем уравнение для функции :

.

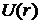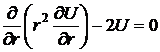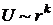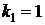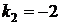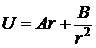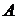Это уравнение решаем, полагая . Несложно получить, что для данной задачи , . Следовательно, , где и 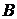- постоянные, которые необходимо определить из граничных условий.

Поскольку 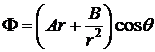, из первого граничного условия следует, что 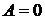, из второго находим: 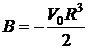. Таким образом,

.

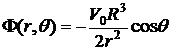Для определения компонент вектора скорости, необходимо вспомнить, что 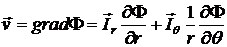. Тогда

,

,

.

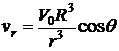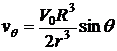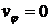Ответ можно выразить через радиус-вектор :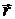

;

.

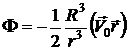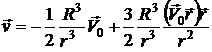2. Найти присоединенную массу шара радиуса 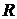, движущегося равноускоренно в идеальной несжимаемой жидкости плотности .

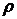Решение: Введем понятие присоединенной массы. Пусть шар массой 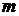движется с постоянным ускорением 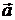. Тогда в момент времени 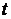его скорость равна 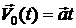, при этом предполагается, что 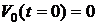. Путь, пройденный телом за это время, запишем как 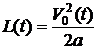. Работа внешней силы 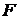, идущая на повышение кинетической энергии шара и жидкости, находится следующим образом: 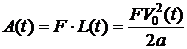. Поскольку в начальный момент времени шар и жидкость покоились, то есть их суммарная кинетическая энергия была равна нулю, имеем:

,

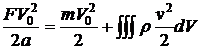здесь 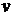- скорость движения жидкости, а интегрирование ведется по всему объему жидкости (для данной задачи 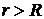). Отсюда следует, что силу 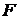можно представить как

,

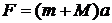где 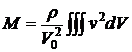- присоединенная масса.

Для вычисления присоединенной массы шара можно воспользоваться результатом решения задачи 4.6.

Ответ: .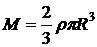

3. Каково ускорение сферического газового пузырька в начале его всплытия в идеальной однородной тяжелой несжимаемой жидкости?

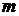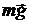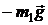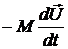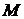Решение: В начале всплытия на пузырек массы действует сила тяжести , сила Архимеда и сила сопротивления жидкости , где - присоединенная масса пузырька, 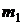- масса жидкости в объеме пузырька. Уравнение его движения имеет вид:

,

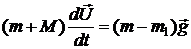следовательно,

.

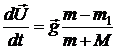Пренебрегая массой пузырька, приближенно получим, что .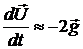

Задачи для самостоятельного решения

4.1. Доказать, что для того, чтобы движение идеальной баротропной жидкости было потенциальным (безвихревым), объемные силы должны иметь потенциал. Показать, что в этом случае уравнения движения имеют интеграл

-

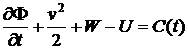интеграл Коши-Лагранжа, где 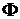- потенциал скорости: 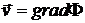, 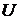- потенциал массовых сил: 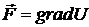, , 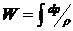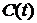- произвольная функция времени.

4.2. Сформулировать условия, при которых интеграл Коши-Лагранжа (см. предыдущую задачу) переходит в уравнение Бернулли.

4.3. Написать систему уравнений, определяющую потенциал скоростей 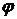и давление 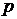при стационарном потенциальном течении однородной несжимаемой жидкости.

Ответ: , .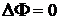

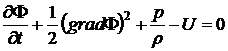4.4. Показать, что функция

,

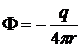где 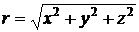, является потенциалом скорости несжимаемой жидкости, имеющим особенность в начале координат ( 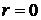). Изучить это движение, найти вектор скорости. Вычислить объем жидкости 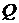, протекающей за единицу времени через поверхность сферы радиуса r с центром в начале координат.

Указание: проверить, что при 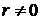функция 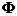удовлетворяет уравнению Лапласа.

Ответ: , .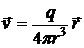

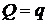4.5. Доказать, что функция

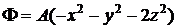
удовлетворяет уравнению Лапласа. Найти компоненты скорости.

Ответ: , , .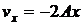

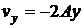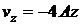4.6. Пусть поле скорости неограниченного объема идеальной несжимаемой жидкости обусловлено движением в ней твердого тела, форма и размеры которого известны.

а) Сформулировать краевую задачу для потенциала поля скорости, считая, что движение потенциально и непрерывно всюду вне тела, а на бесконечности среда покоится.

б) Показать, что поле скоростей жидкости в каждый момент времени определяется только распределением скорости точек поверхности тела в этот момент и не зависит, например, от ускорения тела.

в) Справедливо ли свойство поля скорости, указанное в п. б), для давления?

Ответ: В каждый момент времени 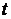значение 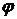определяется из решения внешней задачи Неймана всюду вне тела: 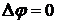, , 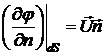, 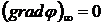где 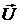- скорость поверхности тела 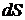, и поэтому зависит лишь от формы тела и нормальной составляющей скорости точек его поверхности. Последнее утверждение справедливо также для 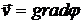, но в общем случае не справедливо для 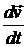, а, следовательно, и для давления.

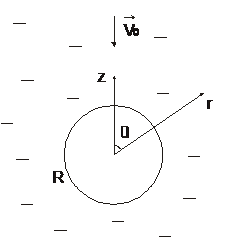
4.7. Решить задачу об обтекании неподвижной сферы радиуса 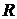потенциальным потоком идеальной несжимаемой жидкости со скоростью 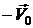. Получить выражение для тангенциальной и радиальной компонент скорости движения частиц жидкости.

Ответ: ,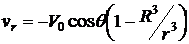

.

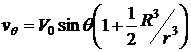4.8. 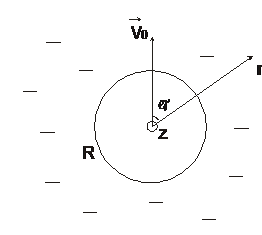Круговой цилиндр радиуса 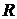движется с постоянной скоростью 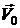в идеальной несжимаемой жидкости в направлении, перпендикулярном его оси. Поставить краевую задачу для уравнения Лапласа. Получить выражение для потенциала 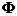и компонент скорости частиц жидкости.

Ответ: ;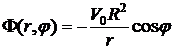

,

,

.

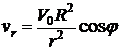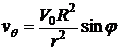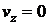4.9. Найти распределение давления на поверхности сферы радиуса 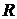, обтекаемой потенциальным потоком идеальной несжимаемой жидкости плотности 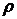, имеющим на бесконечности скорость 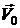и давление 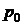. Определить полную силу 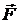, действующую со стороны потока на сферу.

Ответ: 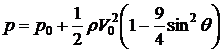; 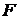=0.

4.10. Шар радиуса 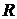и массой 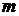движется поступательно и прямолинейно вдоль оси 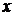со скоростью 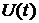в покоящейся идеальной несжимаемой жидкости. Используя интеграл Коши - Лагранжа, найти силу сопротивления жидкости движению шара 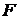и общую кинетическую энергию системы (шар и жидкость) .

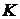Ответ: 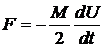; 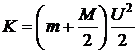, где .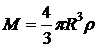

4.11. Показать, что при равномерном движении шара в покоящейся идеальной несжимаемой жидкости шар не испытывает сопротивления (парадокс Д’Аламбера - Эйлера).

4.12. а) В бесконечной цилиндрической трубе, заполненной несжимаемой идеальной жидкостью, с постоянной скоростью движется твердое тело. Далеко перед и за телом жидкость покоится, движение жидкости в системе, связанной с телом, установившееся, массовые силы отсутствуют. Действует ли на тело сила реакции жидкости: сопротивление, подъемная сила?

б) Пусть в трубе движется не одно, а несколько тел с одинаковыми скоростями. Остальные условия те же, что и в п. А). Что можно сказать о силе реакции жидкости на эти тела?

в) За движущимся в трубе телом образовалась конечная полость, заполненная газом, паром или жидкостью. Чему равно сопротивление тела?

Ответ: а) Сопротивление — это составляющая силы, действующей со стороны жидкости на тело, параллельная скорости тела; подъемная сила — составляющая, перпендикулярная этой скорости. В рассматриваемом случае сопротивление равно нулю (парадокс Д’Аламбера- Эйлера), подъемная сила может отличаться от нуля.

б) Суммарное сопротивление всех тел равно нулю.

в) Сопротивление тела вместе с полостью равно нулю.

4.13. Найти присоединенную массу на единицу длины кругового цилиндра радиуса 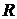, движущегося с ускорением в идеальной несжимаемой жидкости плотности 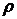в направлении, перпендикулярном его оси.

Ответ: .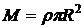

4.14. Тонкостенная сфера (сферический буй) массой 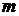и радиусом 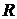находится в равновесии в стратифицированной жидкости плотностью 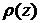на горизонте 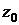. Определить период малых колебаний буя 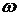, учитывая присоединенную массу.

Ответ: 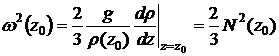, где 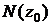- частота Брента-Вяйсяля.

4.15. Пусть жидкость вращается вокруг вертикальной оси так, что частота вращения цилиндрического слоя радиусом 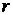равна 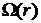. При какой зависимости 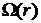движение будет потенциальным?

Ответ: 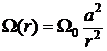, где 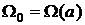, 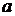- произвольно.

4.16. Найти форму свободной поверхности при потенциальном вращении жидкости в поле силы тяжести.

Указание: использовать решение задачи 4.14 и уравнение Бернулли.

4.17. Показать, что если река имеет закругление, то скорость течения больше около внутреннего берега, а уровень воды – около внешнего. Считать, что оба берега имеют общий центр кривизны, движение идеальной однородной несжимаемой жидкости установившееся и безвихревое.

4.18. Вычислить силу, действующую со стороны жидкости на шар, движущийся в ней со скоростью 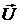, если

а) ;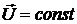

б) .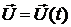

Обтекание шара считать безотрывным. На бесконечности жидкость покоится.

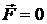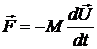Ответ: а) ;б) , где 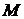- присоединенная масса шара.

4.19. Определить величину и направление силы 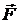, действующей со сторонв жидкости на единицу длины бесконечного кругового цилиндра, движущегося перпендикулярно своей оси со скоростью 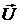, если

а) , ;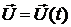

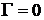б) , .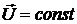

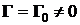Здесь 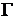- циркуляция скорости по контуру, охватывающему цилиндр. Обтекание цилиндра считать безотрывным.

Ответ: а) ;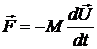

б) ,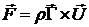

где 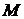- присоединенная масса цилиндра, 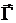- вектор, направленный по оси цилиндра, .

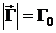Контрольные вопросы

1. Уравнение движения идеальной жидкости. Его представлен6ие в векторонрй форме и в поекциях в декартовой системе координат.

2. Условия потенциального течения жидкости.

3. Потенциальное обтекание шара.

4. Парадок Даламбера – Эйлера.

5. Понятие присоедененной массы.

6. Присоеденная масса сферы и единицы длины бесконечного кругового цилиндра.