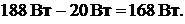Работа и мощность электрического тока. энергетический баланс

Работа, совершаемая электрическим полем при перемещении положитель-

ного заряда Q вдоль неразветвлённого участка a – b электрической цепи, не содержащего источников электрической энергии, равна произведению этого заряда на напряжение 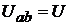между концами участка: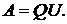

Для оценки энергетических условий важно знать, сколь быстро совершается

работа, т.е. определить мощность

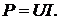(8.1)

Основная единица работы в системе СИ – джоуль (Дж), мощности – ватт (Вт).

Для резистивных элементов выражение (8.1) можно преобразовать, восполь-

зовавшись законом Ома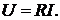

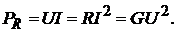(8.2)

Для источника ЭДС, направление которой совпадает с направлением тока

(рис.8.1, а), мощность сторонних сил 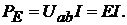Если направления ЭДС

и тока противоположны, то мощность 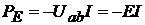(рис. 8.1, б). Аналогич-

но мощность источника тока 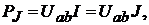если направления тока внутри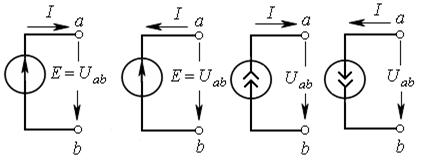

а б в г

Рис. 8.1

источника 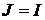и напряжения между его выводами 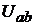противоположны

(рис. 8.1, в). В противном случае мощность 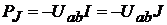(рис. 8.1, г), т. е. источник получает энергию из внешней цепи.

В любой электрической цепи должен соблюдаться энергетический баланс мощностей: алгебраическая сумма мощностей всех источников энергии (в част-

ности, источников тока и источников ЭДС) равна арифметической сумме мощ-

ностей всех приёмников энергии (в частности, резистивных элементов) [3]:

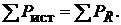, или (8.3)

В качестве примера составим баланс цепи, показанной на рис. 8.2:

Рис. 8.2

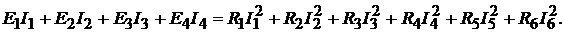
Решение задач приведено в источниках: 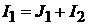: [7, 13, 14, 16].

Пример 9.Для цепи(рис.8.3)заданы: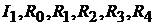и .

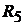Определить:

1) ЭДС источника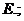

2) токи в остальных ветвях;

3) мощность каждого резистора;

4) составить уравнение баланса мощностей в этой цепи.

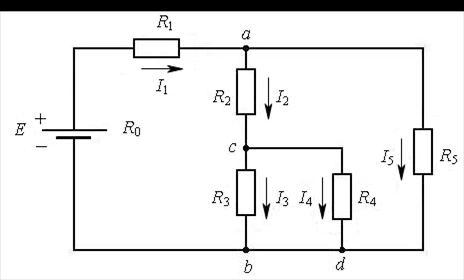
Рис. 8.3

Решение. Ток 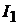проходит через источник и создаёт падение напряжения на

его внутреннем сопротивлении 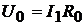и на резисторе с сопротивлением 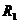, т.е. 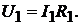Тот же ток 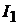создаёт падение напряжения между точками ab, т.е. 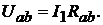ЭДС источника складывается из этих падений напряжения, т.е.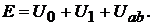

Для определения напряжения между точками 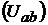и токов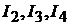

и 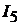произведём преобразование схемы (см. рис. 8.3) и определим общее сопро-

тивление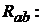

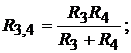
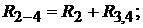
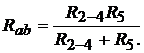
Искомые токи определим по закону Ома:

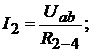
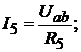
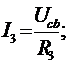
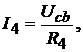
где

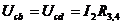или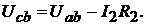

Мощность каждого резистора определяется выражением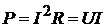

(например: 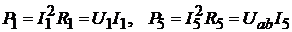и т.д.), а баланс мощностей для цепи (м. рис. 8.3):

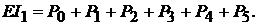
Пример 10.На нагревательном элементе в течение 0,5 ч работы выделилось 550 ккал теплоты. Определить сопротивление элемента, потребляемый им ток, его мощность и затрачиваемую энергию при напряжении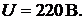

Решение. По закону Джоуля – Ленца 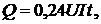откуда

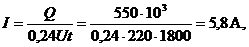
здесь 0,24 − тепловой коэффициент.

Сопротивление нагревателя

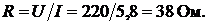
Мощность нагревателя

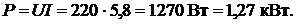
Энергия, потребляемая за 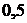ч работы

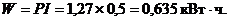
Пример 11. К источнику постоянного тока напряжением 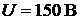подклю-

чена нагрузка, состоящая из четырёх параллельных ветвей. Мощности, потреб-

ляемые каждой ветвью, равны: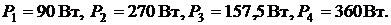

Определить проводимость и ток каждой ветви, общую проводимость и эквива-

лентное сопротивление нагрузки, ток в неразветвлённой части цепи.

Решение. Зная мощность и ток каждой ветви, при заданном значении входно-

го напряжения можно записать 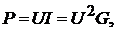так как ток в каждой параллель-

ной ветви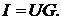

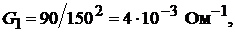
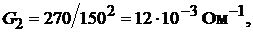
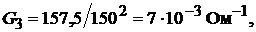
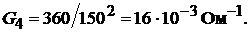
Эквивалентная проводимость нагрузки

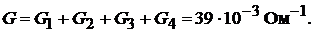
Эквивалентное сопротивление нагрузки

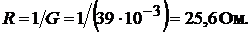
Токи в ветвях определим по формуле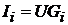

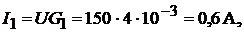
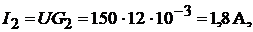
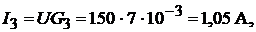
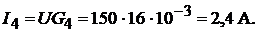
Ток в неразветвлённой части цепи

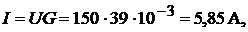
или

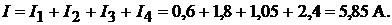
Пример 12. Для цепи, приведённой на рис. 8.4, дано: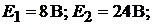

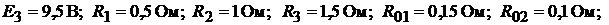
Рис. 8.4

1. Определить величину и направление тока в цепи.

2. Найти потенциалы точек: Б, В, Г, Д, Ж, приняв потенциал точки А равным нулю .

3. Построить потенциальную диаграмму.

4. Составить и проверить баланс мощностей для цепи.

Решение.

1. Выбираем направление обхода контура по часовой стрелке, тогда величи-

на тока

.

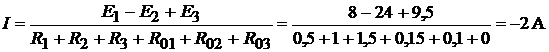Знак «−», полученный в результате вычисления тока, указывает на то, что ток направлен против выбранного направления обхода, т. е. против часовой стрелки (как показано на рис. 8.4). В дальнейших расчётах знак «−» не учиты-

вается. Таким образом, генератор, и 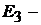потребители.

2. Для определения потенциалов указанных точек обходим контур по направлению тока. При этом получаем ( 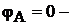по условию):

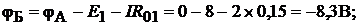
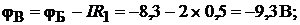
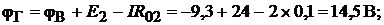
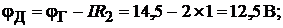
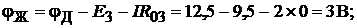
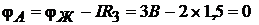В.

3. Для построения потенциальной диаграммы по оси ординат в масштабе от-

кладываются потенциалы точек, а по оси абсцисс – сопротивления участков. Потенциальная диаграмма изображена на рис. 8.5.

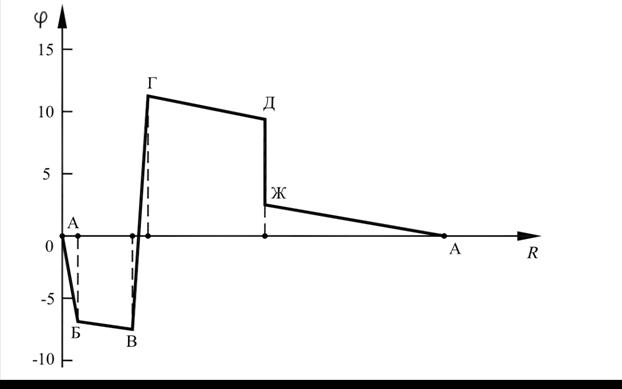
Рис. 8.5

4. Баланс мощностей в электрической цепи с несколькими источниками вы-

полняется при условии, что сумма мощностей источников, работающих в режи-

ме генераторов, равна сумме мощностей источников, работающих в режиме по-

требителей, и потерям мощностей на всех сопротивлениях цепи, включая внут-

ренние сопротивления источников, т.е.

;

;

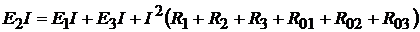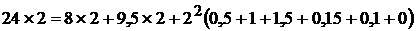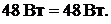
Пример 13. Для схемы на рис. 8.6 дано (табл.):

Номер ветви
В	?	?			?
А	−1	2,2	0,8	−1,4	0,2	1,2	−1
Ом

1. Не определяя ЭДС 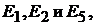найти показания вольтметров.

2. Определив потенциалы узлов, найти ЭДС 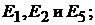проверить вычисле-

ния, составив уравнения по второму закону Кирхгофа, приняв потенциал за-

землённой точки равным нулю.

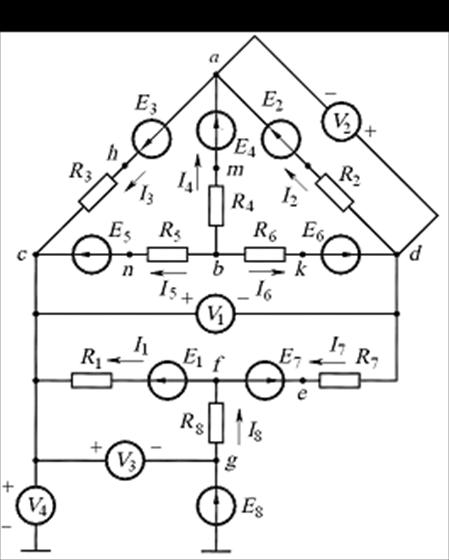
Рис. 8

Решение. 1. Для определения показания вольтметров найдём потенциалы уз-

лов и точек :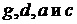

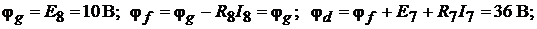
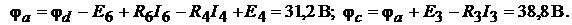
Показания вольтметров: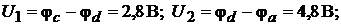

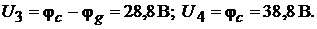
2. Определим значения ЭДС: 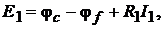т.е. 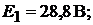аналогич-

но 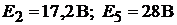. Проверим выполнение второго закона Кирхгофа по

контуру 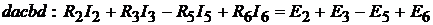, что после под-

становки численных значений даёт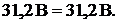

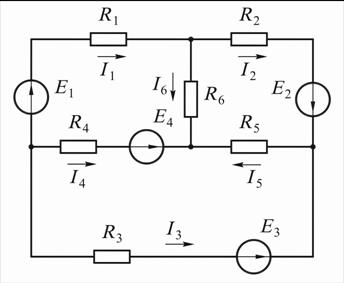
Пример 14.Составить для схемы, изображенной на рис. 8.7, систему уравне-

ний по законам Кирхгофа для определения неизвестных токов.

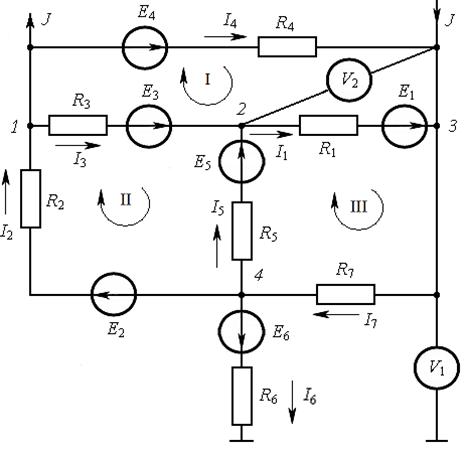
Рис. 8.7

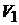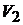Решение. Считаем, что в тупиковой ветви, содержащей сопротивление R₆ , и в ветвях, содержащих вольтметры и , тока нет. По первому закону Кирх-

гофа составляем 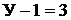независимые узловые уравнения для узлов 1, 2, 3:

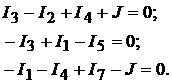
По второму закону Кирхгофа составляем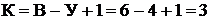

контурные уравнения. Для контуров данные уравнения имеют вид:

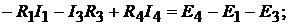
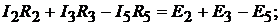
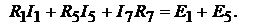
МЕТОД КОНТУРНЫХ ТОКОВ

Метод контурных токов позволяет уменьшить число совместно решаемых

уравнений до 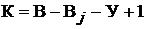. Основан на применении второго закона Кирх-

гофа [1, 3, 6, 7, 9, 11, 12, 14].

Рассмотрим сущность метода сначала для расчёта схемы без источников то-

ка, т. е. при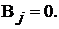

1) выбираем 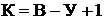независимых контуров и положительных направ-

лений так называемых контурных токов, каждый из которых протекает по всем

элементам соответствующего контура. Достаточным условием выделения 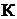независимых контуров является наличие в каждом из них хотя бы одной вет-

ви, принадлежащей только этому контуру;

2) для 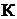независимых контуров составляем уравнения по второму закону

Кирхгофа, совместное решение которых определяет все контурные токи.

3) ток каждой ветви определяем по первому закону Кирхгофа как алгебраи-

ческую сумму контурных токов в соответствующей ветви.

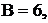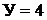В качестве примера рассмотрим расчёт цепи на рис. 9.1, а с числом ветвей узлов , независимых контуров 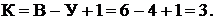Выбира-

ем независимые контуры 1–3 и положительные направления контурных

токов в них 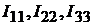(рис.9.1, б). В отличие от токов ветвей каждый контур-

ный ток обозначим двойным индексом номера контура.

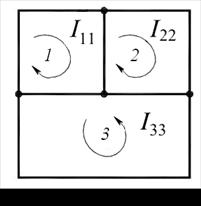
а б

Рис. 9

Уравнения по второму закону Кирхгофа.

Контур 1: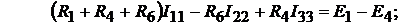

контур 2: 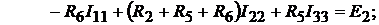(9.1)

контур 3: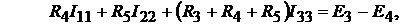

или в матричной форме

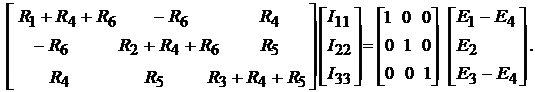(9.2)

Перепишем эти уравнения следующим образом:

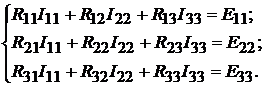(9.3)

Здесь 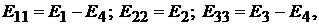где 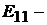контурная ЭДС пер-

вого контура, равная алгебраической сумме ЭДС этого контура; 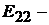контур-

ная ЭДС второго контура; 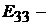контурная ЭДС третьего контура.

Решение системы уравнений (9.1) методом подстановок или (9.2) численны-

ми методами на ЭВМ определяет контурные токи 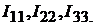Токи ветвей (см. рис. 9.1) находим по первому закону Кирхгофа:

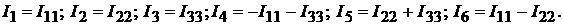
Из выражений (9.1) и (9.2) очевиден принцип составления уравнений по ме-

тоду контурных токов. В левой части уравнений коэффициент при контурном токе рассматриваемого контура положителен и равен сумме сопротивлений его ветвей. Коэффициенты при контурных токах в контурах, имеющих общие вет-

ви с рассматриваемым контуром, равны сумме сопротивлений общих ветвей со знаком плюс (минус), если направления контурных токов в общих ветвях совпадают (противоположны). Правая часть уравнений содержит алгебраичес-

кую сумму ЭДС ветвей рассматриваемого контура, причём слагаемое записыва-

ется со знаком плюс (минус), если направления ЭДС и положительное направ-

ление контурного тока совпадают (противоположны).

Общее решение системы n уравнений относительно тока 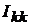может быть

также записано в виде:

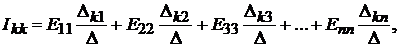(9.4)

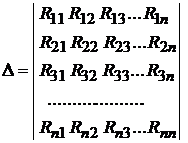где (9.5)

есть определитель системы.

Алгебраическое дополнение 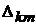получено из определителя 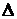путём вычёр-

кивания k-го столбца и m-й строки и умножения полученного определителя

на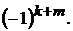

При расчёте схемы замещения с источниками тока возможны упрощения. Контурный ток, выбранный так, что других контурных токов в ветви с источ-

ником тока нет, известен. Поэтому в схеме с 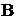ветвями, 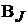из которых содер-

жат источники тока, число независимых контуров без источников тока и соот-

ветствующих им неизвестных контурных токов равно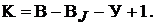

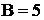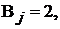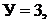Например, в цепи на схеме рис. 9.2 число ветвей с источниками тока узлов независимых контуров без источников тока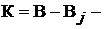 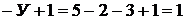(контур 3).

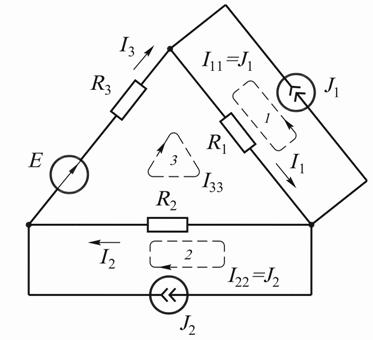
Рис. 9.2

Уравнение по второму закону Кирхгофа для контура 3 при выбранных поло-

жительных направлениях контурных токов:

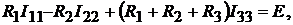
т.е.

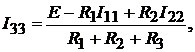
где 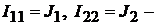известные токи контуров 1 и 2. Токи ветвей:

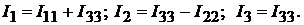
Пример 15.В схеме, изображённой на рис. 9.3, определить токи 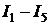в ветвях, напряжения 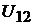и 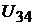между точками 1 – 2 и 3 – 4 цепи. Соста-

вить уравнение баланса мощностей. ЭДС источника питания 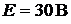(внут-

ренним сопротивлением источника пренебречь), ток источника тока 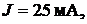сопротивления резисторов: .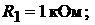

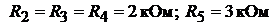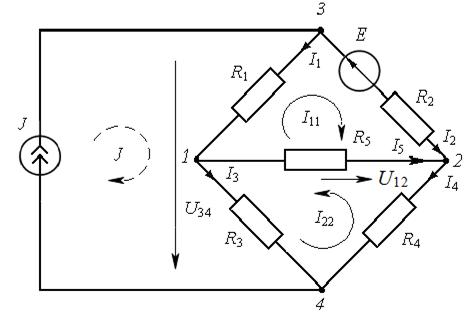
Рис. 9.3

Решение. Условные положительные направления контурных токов в данной электрической цепи принимаем соответствующими рис. 9.3 (показаны сплош-

ными и пунктирными линиями).

По второму закону Кирхгофа составляем уравнение для правого верхнего контура электрической цепи (обход контура по ходу часовой стрелки):

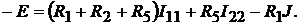
То же для правого нижнего контура:

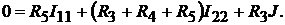
После подстановки значений параметров (ЭДС источника питания, сопро-

тивлений, тока источника тока) получим:

Ток 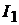совпадает с направлением большего тока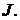

Ток в ветви резистора 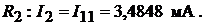Ток в ветви резистора

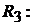
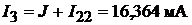. Ток в ветви резистора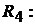 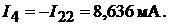Ток в ветви резистора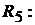 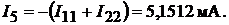Напряжение между узлами 3 и 4 цепи находим из уравнения, составленного в соответствии со вторым законом Кирхгофа для контура 2342: 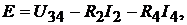откуда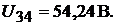

Напряжение между узлами 1 и 2 цепи: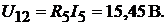

Уравнение баланса мощностей:

,

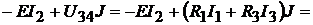
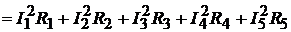откуда после подстановки числовых данных получим тождество:

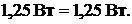
Пример 16.По трёхпроводной линии длиной 500 м. (см. рис. 9.4) от двух генераторов 1 и 2 питаются две группы ламп по 50 Вт, 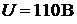. В первой группе 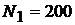ламп, во второй 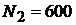ламп. Сечение крайних проводов 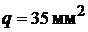, а сечение среднего (нулевого) провода 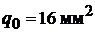. Каждый генератор имеет внутреннее сопротивление 0,01 Ом и развивает ЭДС 120 В. Определить токи во всех проводах линии и напряжение на зажимах каждой группы ламп, сопротивления которых считать постоянными. Материал провода − медь.

Решение. Определим проводимость одной лампы:

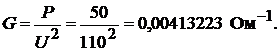
Тогда проводимость 200 ламп равна:

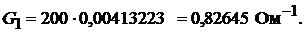
Проводимость 600 ламп равна:

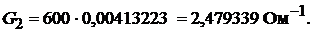
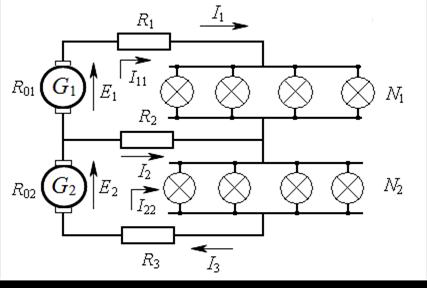
Рис. 9.4

Соответственно сопротивление участка, содержащего 200 ламп, равно:

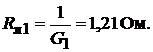
Сопротивление участка, содержащего 600 ламп, равно:

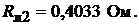
Сопротивления крайних участков линии:

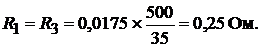
Сопротивление средней (нулевой) линии равно:

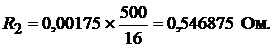
Для определения токов в линиях применим метод контурных токов. Тогда

для верхнего и нижнего контуров получим:

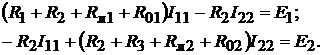
После подстановки численных значений сопротивлений будем иметь:

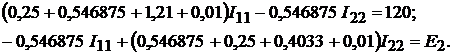
Тогда

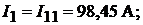
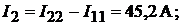
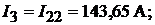
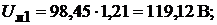
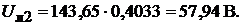
Пример 17. В схеме рис. 9.5 определить все токи методом контурных токов. Дано: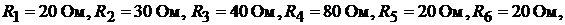

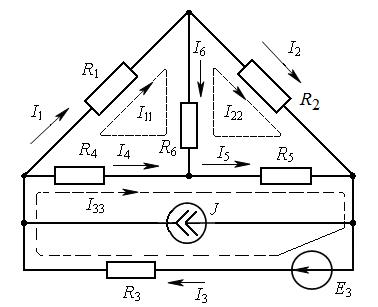
Рис. 9.5

Решение. Выберем контуры для получения независимых уравнений таким образом, чтобы в каждом была по крайней мере одна новая ветвь (показаны на

рис. 9.5 пунктирной линией). Контурными токами будут 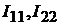и .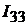

Запишем уравнения для выбранных токов: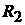

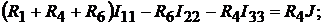
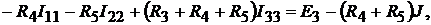
откуда при заданных параметрах находим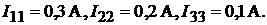

Токи в ветвях: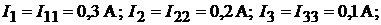

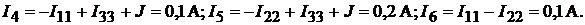
Пример 18.Найти токи в ветвях цепи, изображённой на рис. 9.6, где

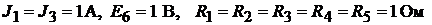
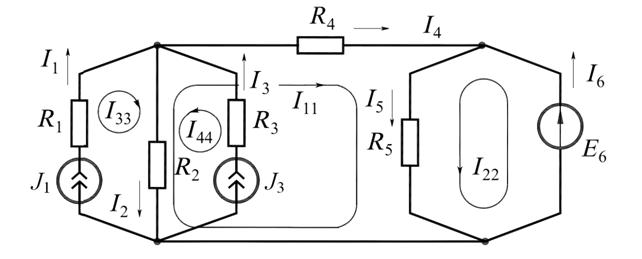
Рис. 9.6

Решение. В цепи четыре независимых контура. В двух ветвях имеются ис-

точники тока с известными токами. Если через каждую из этих ветвей замк-

нуть по одному контурному току, то эти контурные токи автоматически станут известными:

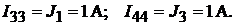
Для определения двух других независимых контурных токов составляем два уравнения:

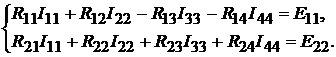
Определяем коэффициенты:

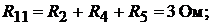
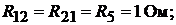
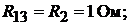
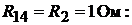
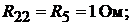
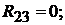
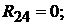
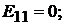
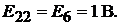
Подставим коэффициенты в левую и правую части вышеуказанного уравне-

ния, получим:

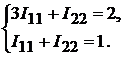
Решив данное уравнение, найдём контурные токи :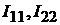

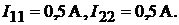
Определяем истинные токи в ветвях:

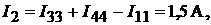
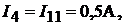
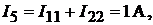
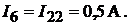
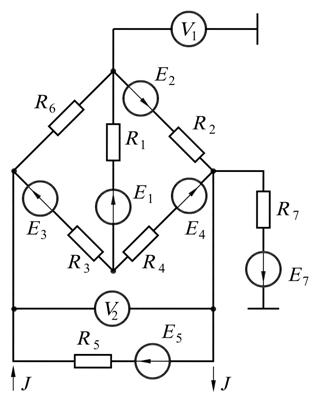
Пример 19.Рассчитаем параметры электрической цепи, схема которой при-

ведена на рис. 9.7, а. Параметры схемы:

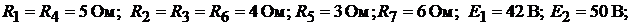
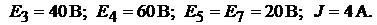
Решение. В схеме четыре узла и шесть ветвей, не содержащих ис-

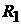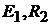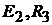
точников тока . Это ветви, состоящие из элементов и 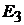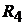и

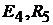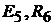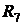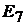и , и и . В ветви с элементами и тока нет, так как она замыкается на ветвь с вольтметром, сопротивление которого считается беско-

нечно большим. Необходимо определить значения силы тока .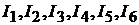

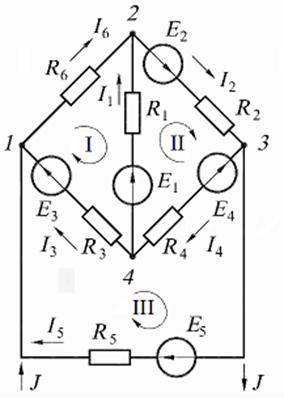
Нумерация узлов, произвольно выбранные положительные направления токов и обходов контуров показаны на рис. 9.7, б.

а б

Рис. 9.7

1.По первому закону Кирхгофа составляем 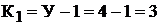независмые узловые уравнения для узлов 1, 2 и 3:

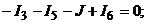
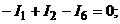
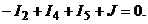
По второму закону Кирхгофа составляем 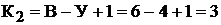кон-

турные уравнения. Для контуров (см. рис. 9.7, б) уравнения имеют вид:

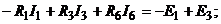
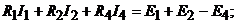
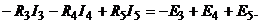
2. Контуры и направления контурных токов в них показаны на рис. 9.8. Кон-

тур с известным контурным током проведём по ветви с элементами .

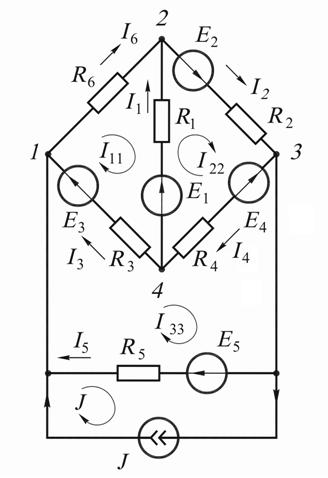
Рис. 9.8

Система уравнений для контурных токов 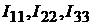имеет вид:

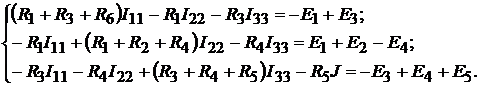
Подставив известные числовые значения, получим:

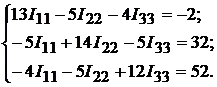
Отсюда получим значения контурных токов: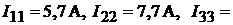

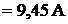. Далее определим силу тока в ветвях:

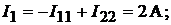
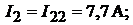
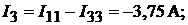
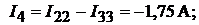
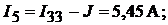
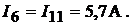
Поскольку значения токов рассчитаны методом контурных токов, то первый закон Кирхгофа выполняется автоматически. Чтобы убедиться в правильности решения проверим тождественность уравнений, составленных по второму зако-

ну Кирхгофа для контуров 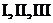, (см. рис. 9.7, б) подставляя в них числовые значения:

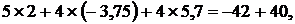или

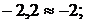
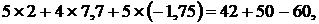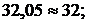
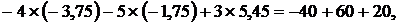или

или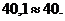

3. Уравнение баланса мощностей для схемы на рис. 9.8 имеет вид

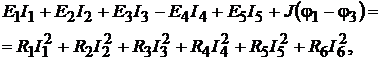
где 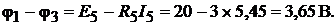Левая часть уравнения учитыва-

ет мощность источников, правая − мощность, потребляемую сопротивления-

ми. Подставив численные значения, получим для левой части:

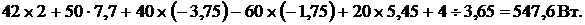
для правой:

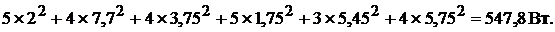
Сравним полученные значения: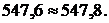

4.Напряжение, измеряемое вольтметром , включённым в соответствии с рис. 9.7, а, составляет

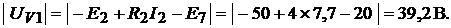
Для вольтметра :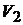

Пример 20.Для обобщённой цепи, приведённой на рис. 9.9, требуется вы-

полнить расчёт цепи с использованием одного из способов расчёта цепи, рас-

считать напряжение между точками A и B схемы, а также составить баланс мощностей для исходной схемы.

Дано: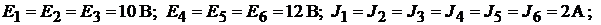

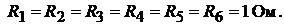
Решение. Проводим расчет схемы с использованием метода контурных то-

ков. Условные направления принятых контурных токов приведены на рис. 9.9.

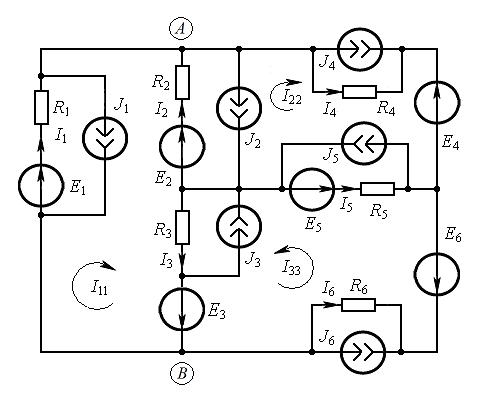
Рис. 9.9

Cистема уравнений, позволяющая определить контурные токи 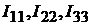, примет вид:

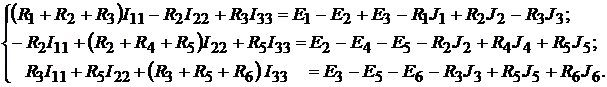
После подстановки численных величин, получим:

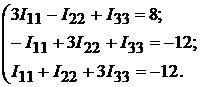
Данные контурные токи равны: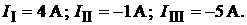

Тогда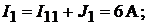

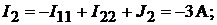
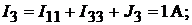
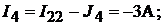
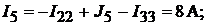
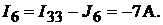
Напряжение между точками A и B схемы:

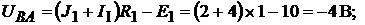
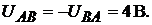
Составим баланс мощностей для исходной схемы.

Мощность, отдаваемая в цепь источниками ЭДС:

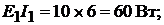
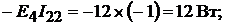
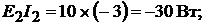
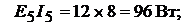
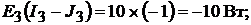
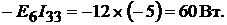
Всего: 188 ВТ.

Мощность, отдаваемая в цепь источниками тока:

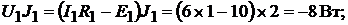
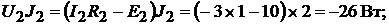
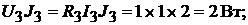
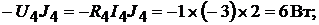
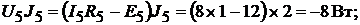
Всего: −20Вт.

Мощность приёмников энергии:

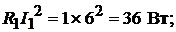
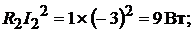
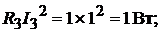
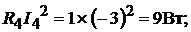
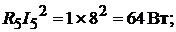
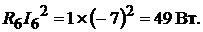
Всего: 168 Вт.

Баланс энергии: