Проверка репрезентативности выборки (случайного отбора данных)
Если параметры нормальной генеральной совокупности известны нам изначально, критерий χ2 может проверить случайный характер нашей выборки. Действительно, репрезентативная (случайная) выборка не должна изменять характера распределения случайной величины.
Будем использовать критерий согласия Пирсона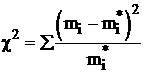 
.
Проверяемая гипотеза состоит в том, что выборка 150 изделий имеет нормальное распределение. Уровень значимости выберем равным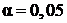 
.
Расчет ведем на листе «Пирсон». Теоретические частоты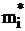 
для рассматриваемого распределения 150 изделий, взятых из генеральной совокупности с μ = 60 и σ = 10, приведены в таблице 8. Порядок вычисления объясняют заголовки каждого из столбцов этой таблицы.
Таблица 8. Расчет теоретических частот для выборки 150 изделий, взятых из нормальной генеральной совокупности (μ=60; σ=10; n=150;ΔX=6,5)
| Диапазон | Интеграл вероятности | Первая разность | Частота | ||
 |  |  |  |  |  |
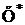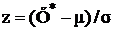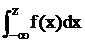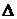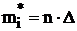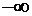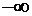| .... |  | | 0,0006298 | 0,0944795 | |
| 27,75 | -3,225 | 0,000629863 | |||
| 27,75 | -3,225 | 0,000629863 | 0,0043821 | 0,6573211 | |
| 34,25 | -2,575 | 0,005012004 | |||
| 37,5 | 34,25 | -2,575 | 0,005012004 | 0,0221026 | 3,3154012 |
| 40,75 | -1,925 | 0,027114679 | |||
| 40,75 | -1,925 | 0,027114679 | 0,0740399 | 11,105991 | |
| 47,25 | -1,275 | 0,101154621 | |||
| 50,5 | 47,25 | -1,275 | 0,101154621 | 0,1648309 | 24,724636 |
| 53,75 | -0,625 | 0,265985529 | |||
| 53,75 | -0,625 | 0,265985529 | 0,2439869 | 36,598048 | |
| 60,25 | 0,025 | 0,509972518 | |||
| 63,5 | 60,25 | 0,025 | 0,509972518 | 0,2401895 | 36,02843 |
| 66,75 | 0,675 | 0,750162118 | |||
| 66,75 | 0,675 | 0,750162118 | 0,1572523 | 23,587846 | |
| 73,25 | 1,325 | 0,907414424 | |||
| 76,5 | 73,25 | 1,325 | 0,907414424 | 0,0684515 | 10,267725 |
| 79,75 | 1,975 | 0,975865926 | |||
| 79,75 | 1,975 | 0,975865926 | 0,0198016 | 2,9702438 | |
| 86,25 | 2,625 | 0,995667552 | |||
| .... | 86,25 | 2,625 | 0,995667552 | 0,0043324 | 0,6498672 |
 | | ||||
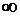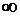| Сумма | 0,9993701 | 149,90552 |
Значения в первой и последней строчках 2 и 3-го столбцов равны соответственно -∞ и +∞, так как нормальное распределение теоретически простирается от -∞ до +∞. Числа, указанные в 4-м столбце, получены с помощью функции «НОРМСТРАСП». В 6-м столбце приведены первые разности.
Вычисление значения χ2=4,583 проведено в таблице 9. В этой таблице показаны восемь групп (интервалов), то есть на три группы меньше, чем в таблице 8. Сокращение числа групп осуществлено за счёт объединения первых трех, а также двух последних групп. Это сделано потому, что значения m* в первых трех и последних двух группах весьма малы. Существует правило, указывающее, что критерий χ2 может применяться в тех случаях, когда каждая теоретическая группа содержит по крайней мере пять наблюденных значений, а общее количество наблюденных значений составляет по крайней мере 50. Введение этих ограничений имеет целью гарантировать, что распределение наблюденных значений mi относительно значений теоретических частот 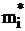будет настолько близко к нормальному, что применение при оценке вероятностей таблиц для χ2 будет вполне обоснованным.
Таблица 9. Вычисление критерия χ2
| Границы теоретических интервалов | m | m* | m - m* | (m - m*)2 |  |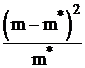
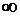| - ÷ 40,75 | 4,067 | 0,93279813 | 0,871 | 0,214 | |
| 40,75 ÷ 47,25 | 11,106 | 0,89400872 | 0,799 | 0,072 | |
| 47,25 ÷ 53,75 | 24,724 | -8,72463621 | 76,11 | 3,079 | |
| 53,75 ÷ 60,25 | 36,598 | 3,40195163 | 11,57 | 0,316 | |
| 60,25 ÷ 66,75 | 36,028 | -1,0284399 | 1,06 | 0,029 | |
| 66,75 ÷ 73,25 | 23,588 | 4,41215398 | 19,47 | 0,825 | |
| 73,25 ÷ 79,75 | 10,268 | -0,26772525 | 0,07 | 0,007 | |
| 79,75 ÷ 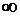| 3,620 | 0,3798889 | 0,14 | 0,040 | |
| Всего | 150,00 | 110,10 | 4,583 |
Хотя таблица 9 содержит восемь групп, имеется только семь степеней свободы (ν=R–1=8–1=7), так как на теоретические частоты накладывается одно ограничение: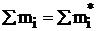 
.Воспользовавшись функцией ХИ2ОБР(a; 
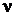) для a=0,05 и ν=7, находим: 
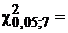14,07.
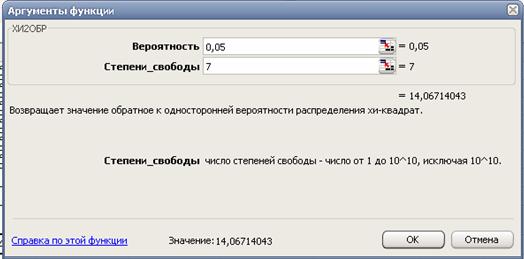
Итак, область принятия проверяемой гипотезы будет определяется соотношением χ2 < 14,07, а область отклонения – соотношением χ2 ≥ 14,07. Так как вычисленное значение χ2 составляет 4,583, то оно попадает в область принятия, в связи с чем можно принять гипотезу о том, что выборка имеет нормальное распределение, т.е. осуществлялась по случайному закону.
Проверка гипотезы о нормальном распределении
Генеральной совокупности
Рассмотрим теперь ситуацию, как будто бы нам изначально не были известны параметры распределения генеральной совокупности, но можно считать, что выборка взята по случайному закону.
В этом случае появляется возможность проверить гипотезу о том, что генеральная совокупность является нормальной. При этом снова примем α = 0,05.
Так как параметры µ и s основного распределения теперь нам неизвестны, используем совместные оценки максимума правдоподобия, исчисленные на основании группировки (таблица 3). Такими оценками являются выборочная средняя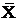 
для математического ожидания μ и исправленная выборочная дисперсия 
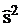для дисперсии 
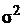. По формулам 
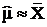и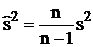 
, находим: 
; 
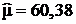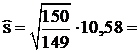10,62
В таблице 10, рассчитанной на листе «Пирсон 2» аналогично таблице 8, показано вычисление теоретических частот, а из таблицы 11 (аналог таблицы 9) по формуле 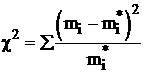находим χ2 = 4,59.
Таблица 10. Вычисление нормальных частот для выборки 150 изделий с параметрами: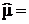 
60,38; 
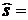10,62
| Диапазон | Интеграл вероятности | Первая разность | Частота | ||
| | | | | | |
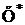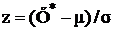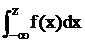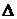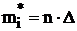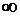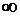| .... | - | - | 0,00106135 | 0,15920286 | |
| 27,75 | -3,073 | 0,00106135 | |||
| 27,75 | -3,073 | 0,00106135 | 0,00587675 | 0,88151319 | |
| 34,25 | -2,460 | 0,00693811 | |||
| 37,5 | 34,25 | -2,460 | 0,00693811 | 0,0253342 | 3,80012951 |
| 40,75 | -1,848 | 0,03227230 | |||
| 40,75 | -1,848 | 0,03227230 | 0,07589259 | 11,3838885 | |
| 47,25 | -1,236 | 0,10816489 | |||
| 50,5 | 47,25 | -1,236 | 0,10816489 | 0,15805244 | 23,7078658 |
| 53,75 | -0,624 | 0,26621733 | |||
| 53,75 | -0,624 | 0,26621733 | 0,22889932 | 34,3348973 | |
| 60,25 | -0,012 | 0,49511665 | |||
| 63,5 | 60,25 | -0,012 | 0,49511665 | 0,23056748 | 34,5851215 |
| 66,75 | 0,600 | 0,72568412 | |||
| 66,75 | 0,600 | 0,72568412 | 0,16153373 | 24,2300597 | |
| 73,25 | 1,212 | 0,88721786 | |||
| 76,5 | 73,25 | 1,212 | 0,88721786 | 0,07869984 | 11,8049766 |
| 79,75 | 1,824 | 0,96591770 | |||
| 79,75 | 1,824 | 0,96591770 | 0,02665634 | 3,99845091 | |
| 86,25 | 2,436 | 0,99257404 | |||
| .... | 86,25 | 2,436 | 0,99257404 | 0,00742596 | 1,11389412 |
| | | ||||
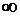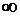| Сумма |
Таблица 11. Вычисление χ2 для выборки 150 изделий с параметрами: 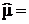60,38; 
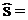10,62
| Границы теоретических интервалов | m | m* | m - m* | (m - m*)2 | |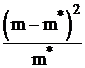
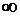| - ÷ 40,75 | 4,84084 | 0,15915443 | 0,025330 | 0,00523258 | |
| 40,75 ÷ 47,25 | 11,3838 | 0,61611151 | 0,379593 | 0,03334479 | |
| 47,25 ÷ 53,75 | 23,7078 | -7,70786578 | 59,41119 | 2,50596977 | |
| 53,75 ÷ 60,25 | 34,3348 | 5,66510268 | 32,09338 | 0,93471631 | |
| 60,25 ÷ 66,75 | 34,5851 | 0,41487848 | 0,172124 | 0,00497683 | |
| 66,75 ÷ 73,25 | 24,2300 | 3,76994035 | 14,21245 | 0,58656274 | |
| 73,25 ÷ 79,75 | 11,8049 | -1,80497664 | 3,257940 | 0,27598027 | |
| 79,75 ÷ 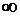| 5,11234 | -1,11234503 | 1,237311 | 0,24202425 | |
| Всего | 150,00 | -2,6645E-15 | 110,7893 | 4,58880754 |
При этой проверке критерий χ2 имеет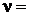 
5 степеней свободы, а 3 степени свободы потеряны, так как согласование наблюденных и теоретических частот осуществлялось из трёх условий:
; 
; 
.
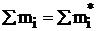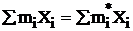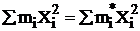Это означает, что из 8 групповых частот любые пять можно взять случайно или произвольно, но выбор 3-х остальных групповых частот нельзя осуществлять произвольно, т.к. наблюденные и теоретические распределения должны иметь одинаковые количество элементов, средние и стандартные отклонения.
Воспользовавшись функцией ХИ2ОБР(a; 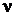), находим 
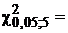11,07. Значит, область принятия определяется соотношением χ2 < 11,07.
Так как вычисленное значение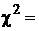 
4,59 лежит в области принятия, гипотеза Н0, что генеральная совокупность, из которой взята эта случайная выборка, является нормальной, не отвергается.