Комбинаторный метод вычисления вероятностей
Правило произведения
Если первое событие может произойти n1 способами, а второе - n2 способами независимо от первого, то совместная реализация может произойти n1×n2 способами.
Правило суммы
Если первое событие может произойти n1 способами, а второе - n2 способами независимо от первого, то первое или второе события могут произойти n1+n2 способами.
Комбинаторный метод вычисления вероятностей
При подсчете числа элементарных исходов, составляющих события в классической схеме, часто используются известные формулы комбинаторики. Каждая из комбинаторных формул определяет общее число элементарных исходов в некотором идеализированном эксперименте по выбору наудачу m элементов из n различных элементов исходного множества E = {e1, e2, ..., en}.
При постановке каждого такого эксперимента строго оговорено, каким способом производится выбор и что понимается под различными выборками. Существуют две принципиально отличные схемы выбора: в первой схеме выбор осуществляется без возвращения элементов (это значит, что отбираются либо сразу все m элементов, либо последовательно по одному элементу, причем каждый отобранный элемент исключается из исходного множества). Во второй схеме выбор осуществляется поэлементно с обязательным возвращением отобранного элемента на каждом шаге и тщательным перемешиванием исходного множества перед следующим выбором. После того, как выбор тем или иным способом осуществлен, отобранные элементы (или их номера) могут быть либо упорядочены (т.е. выложены в последовательную цепочку), либо нет. В результате получаются следующие четыре различные постановки эксперимента по выбору наудачу m элементов из общего числа n различных элементов множества Е.
А. Схема выбора, приводящая к сочетаниям
Если опыт состоит в выборе m элементов без возвращения и без упорядочивания, то различными исходами следует считать m-элементные подмножества множества E, имеющие различный состав. Получаемые при этом комбинации элементов (элементарные исходы) носят название сочетания из n элементов по m, а их общее число N(W) определяется по формуле:
Cmn = n!/[m!(n - m)!] = n(n - 1)...(n - m + 1)/m!.
Для чисел Cmn, называемых также биномиальными коэффициентами, справедливы следующие тождества, часто оказывающиеся полезными при решении задач:
Cmn = Cn-mn (свойство симметрии),
Ckn+1 = Ckn + Ck-1n; C0n = 1 (рекуррентное соотношение),
C0n + C1n + ... + Cnn = 2n (следствие биномиальной формулы Ньютона).
Пример 1. Множество Е содержит 10 первых букв русского алфавита. Сколько различных алфавитов из трех букв можно составить из данного множества букв? Какова вероятность того, что случайно выбранный алфавит будет содержать букву «a»?
Решение Число различных алфавитов равно числу трехэлементных подмножеств множества Е (числу сочетаний из 10 элементов по 3): N(W) = C310 = 10×9×8/(1×2×3) = 120.
Пусть событие A - случайно выбранный алфавит из трех букв, содержащий букву «a». Число элементов множества А равно числу всех возможных способов отобрать две буквы из девяти (из десяти букв исключена буква «a»), т.е. равно числу сочетаний из 9 элементов по 2: N(A) = C29 = 9×8/2 = 36.
Таким образом, Р(A) = N(A)/N(W) = 36/120 = 0,3.
Г. Схема выбора, приводящая к размещениям с повторениями
Если выбор m элементов из множества E = {e1, e2, ..., en}, производится с возвращением и с упорядочиванием их в последовательную цепочку, то различными исходами будут всевозможные m-элементные наборы (вообще говоря, с повторениями), отличающиеся либо составом элементов, либо порядком их следования. Например, при m = 4 наборы {e1, e1, e2, e1}, {e2, e1, e1, e1} и {e1, e1, e3, e1} являются различными исходами данного опыта. Получаемые в результате различные комбинации называются размещениями, с повторениями, а их общее число определяется формулой
N(W)= nm.
Пример 4. Опыт состоит в четырехкратном выборе с возвращением одной из букв алфавита E = {а, б, к, о, м} и выкладывании слова в порядке поступления букв. Какова вероятность того, что в результате будет выложено слово «мама»?
Решение. Число элементов множества, равновероятных исходов равно числу размещений с повторениями из 5 элементов по 4 т.е. N(W)= 54. Слову «мама» соответствует лишь один возможный исход. Поэтому Р(A) = N(A)/N(W) = 1/54 » 0,0016.
Случайные величины
Случайной величиной (СВ) Х называется действительная функция X = X(w), определенная на множестве элементарных исходов W, такая, что для любого действительного x множество тех w Î W, для которых X(w) < x, принадлежит полю событий W(W). СВ принято обозначать большими буквами латинского алфавита, а их возможные значения - соответствующими малыми буквами.
Различают СВ дискретного типа (сокращенно СВДТ) и СВ непрерывного типа (сокращенно СВНТ). СВ называется СВДТ, если множество ее возможных значений конечно или счетно. Например, число бросаний монеты до появления герба или число выпавших очков при бросании игрального кубика. СВ называется СВНТ, если множество ее возможных значений заполняют интервал числовой оси. Например, время до отказа прибора (время “жизни” прибора) или погрешность измерения.
Для полного задания СВ необходимо указать множество ее возможных значений и определить некоторое соответствие между отдельными ее значениями xi(или некоторыми подмножествами) и вероятностями pi, с которыми эти значения (или подмножества) принимаются. Любое такое соответствие называется законом распределения СВ. Например, для СВДТ достаточно указать зависимостьpi = P{X = xi} или таблицу следующего вида:
| Возможные значения СВ Х | x1 | x2 | ... | xn |
| P{X = xi} = pi > 0; (p1 + p2 + ... + pn = 1) | p1 | p2 | ... | pn |
Для СВНТ такие способы не годятся, поэтому ставят в соответствие вероятности не отдельные значения СВ, а множество значений (X < x), где x - произвольное число. Этот способ годится для СВДТ и для СВНТ.
Функцией распределения (ФР) (или интегральным законом распределения) СВ X называется числовая функция F(x) = P{X < x}, определенная для любых x Î R. Свойства ФР:
1. 0 £ F(x) £ 1;
2. F(x1) £ F(x2), если x1 < x2, т.е. F(x) - неубывающая функция;
3. 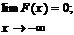
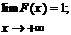
4. P{a £ X < b} = F(a) - F(b).
Плотностью распределения (ПР) (или дифференциальным законом распределения) СВ X называется числовая функция f(x), равная производной от ФР, если такая производная существует: f(x) = F¢(x). Связь между ПР и ФР можно представить в интегральной форме:
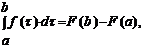 что позволяет определить ФР:
что позволяет определить ФР: 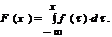
Свойства ПР:
1. f(x) ³ 0, т.к. ФР - неубывающая функция;
2. 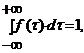 - условие нормировки.
- условие нормировки.
Задача №1. Могут ли функции j(x) и y(x) являться ФР или ПР некоторой СВ X, если “да”, то при каком значении l?
а) j(x) = 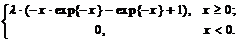 б) y(x) =
б) y(x) = 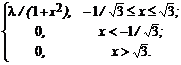
Случайные векторы
Упорядочная совокупность n случайных величин (СВ) Х1, Х2, ..., Хn, рассматриваемых совместно в данном опыте, называется n-мерной СВ или случайным вектором и обозначается 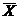 = (Х1, Х2, ..., Хn).
= (Х1, Х2, ..., Хn).
Функцией распределения (ФР) n-мерного случайного вектора называется функция n действительных переменных х1, x2, ..., xn, определяемая как вероятность совместного выполнения n неравенств: F(x1, x2, ... xn) = P{ X1 < x1, X2 < x2,..., Xn < xn}. В частности, для двумерного случайного вектора (X, Y) по определению ФР имеем: F(x, y) = P{X < x, Y < y}. ФР F (х, у) обладает следующими свойствами:
1. 0 £ F(x, у) £ 1;
2. F(x, у) - неубывающая функция своих аргументов;
3. 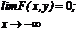
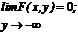
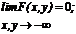
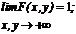
4. 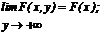
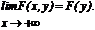
Свойство 4 обычно называют условием согласованности. Оно означает, что ФР отдельных компонент случайного вектора могут быть найдены предельным переходом из функции совместного распределения этих компонент. Вероятность попадания случайной точки на плоскости (X, Y) в прямоугольник со сторонами, параллельными осям координат, может быть вычислена с помощью ФР по формуле:
P{x1 £ X < x2, y1 £ Y < y2} = F(x1, y1)+ F(x2, y2)- F(x1, y2)- F(x2, y1).
Двумерный случайный вектор (X,Y) называется случайным вектором дискретного типа (СВДТ), если множество его возможных значений G(x, y) не более чем счетно. Ее закон распределения можно задать двумерной таблицей из перечня возможных значений пар компонент {(хi, yi) | (хi, yi) Î G(x, y)} и соответствующих каждой такой паре вероятностей pij = P{X = xi, Y = yj}, удовлетворяющих условию 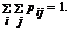
Двумерный случайный вектор (X, Y) называется случайным вектором непрерывного типа (СВНТ), если существует такая неотрицательная функция f(x, y) называемая плотностью распределения (ПР) вероятностей случайного вектора, что:
f(x, y) = 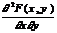 , тогда F(x, y) =
, тогда F(x, y) = 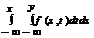 .
.
ПР вероятностей обладает следующими свойствами:
f(x, y) ³ 0, (x, y) Î R2;
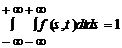 - условие нормировки.
- условие нормировки.
ПР вероятностей отдельных компонент случайного вектора выражаются в виде интегралов от совместной плотности:
f(x) = 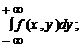 f(y) =
f(y) = 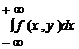 .
.
Вероятность попадания случайной точки в произвольную квадрируемую область S на плоскости определяется по формуле
P{(X, Y) Î S}= 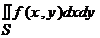 .
.
Условной плотностью распределения вероятностей случайной компоненты X при условии, что компонента Y приняла определенное значение у, называется функция f(x/y) действительной переменной х Î R: f(x/y) = f(x, y)/f(y). Аналогично определяется условная плотностью распределения вероятностей случайной компоненты Y при условии, что компонента X приняла определенное значение x: f(y/x) = f(x, y)/f(x). СВ X1, X2, ..., Хn называются независимыми (в совокупности), если для событий {Xi Î Bi}, i = 1, 2, ..., n, где B1, B2, ... Bn - подмножества числовой прямой, выполняется равенство: P{X1 Î B1, X2 Î B2, ... Xn Î Bn} = P{X1 Î B1}× P{X2 Î B2}× ... ×P{Xn Î Bn}.
Теорема: СВ X1, Х2, .... Хn независимы тогда и только тогда, когда в любой точке x = (x1, x2, ..., xn) имеет место равенство: F(x1, x2, ..., xn) = F(x1) × F (x2) × ... × F (xn) (или f(x1, x2, ..., xn) = f(x1) × f(x2) × ... × f(xn)).
ЗАКОН БОЛЬШИХ ЧИСЕЛ
Следующие утверждения и теоремы составляют основу законов, объединенных общим названием закон больших чисел.
Первое неравенство Чебышева. Если СВ X ³ 0 имеет конечное значение m = M[X], то для любого e > 0 справедливо:
P{X ³ e} £ m/e или P{X < e} > 1 - m/e.
3 Для наглядности проведем доказательство для СВНТ X с ПР f(x), хотя это остается справедливым и для СВДТ. Так как
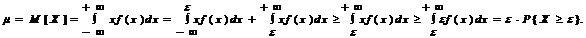
Тогда P{X ³ e} £ m/e, что и требовалось показать. 4
Второе (основное) неравенство Чебышева. Если СВ X имеет конечные значения m = M[X] и s2 = D[X], то для любого e > 0 справедливо:
P{ôX - mô ³ e} £ s2/e2 или P{ôX - mô < e} > 1 - s2/e2.
3 Проведем доказательство для СВНТ X с ПР f(x). Так как
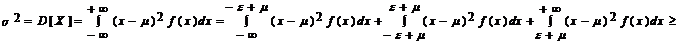
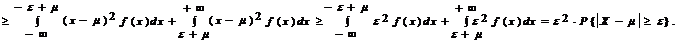
Тогда P{ôX - mô ³ e} £ s2/e2, что и требовалось показать. 4
Последовательность СВ X1, X2, ..., Xn, ... называется сходящийся по вероятности при n ® ¥ к СВ X (обозначение: 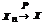 при n ® ¥), если для любого, сколь угодно малого e > 0 справедливо
при n ® ¥), если для любого, сколь угодно малого e > 0 справедливо 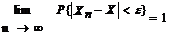 , или, иными словами, для любых, сколь угодно малых чисел e > 0 и d > 0 найдется номер k, что для всех n > k выполняется условие:
, или, иными словами, для любых, сколь угодно малых чисел e > 0 и d > 0 найдется номер k, что для всех n > k выполняется условие:
P{ôXn - Xô < e} > 1 - d.
Теорема (Закон больших чисел в форме Чебышева). Если попарно независимые СВ X1, X2, ..., Xn, ... имеют конечные значения M[Xi] = mi и D[Xi] = si2£ s2, то для любого e > 0 справедливо следующее:
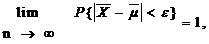 где
где 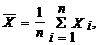
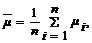 или
или 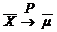 при n ® ¥.
при n ® ¥.
3 Пусть СВ 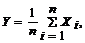 следовательно математическое ожидание и дисперсия этой СВ определяется следующим образом
следовательно математическое ожидание и дисперсия этой СВ определяется следующим образом
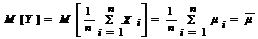 и
и 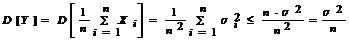 .
.
Из второго неравенства Чебышева следует, что P{ôY - M[Y]ô < e} > 1 - D[Y]/e2 ³ 1 - c2/n, где c = s/e > 0.
Тогда при n ® ¥ для любого e > 0 вероятность P{ô 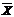 -
- 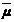 ô < e} ® 1, что и требовалось показать. 4
ô < e} ® 1, что и требовалось показать. 4
Следствие. Если в условии теоремы СВ X1, ..., Xn, ... имеют одинаковые значения M[Xi] = m, то для любого e > 0 справедливо следующее:
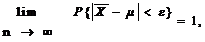 где
где 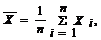 или
или 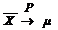 при n ® ¥.
при n ® ¥.
Теорема (Закон больших чисел в форме Бернулли). Пусть СВ К - число “успехов” в n испытаниях по схеме Бернулли. Тогда при n ® ¥ частота “успехов” сходится по вероятности к p, где p - вероятность “успеха” в одном испытании, т.е.:
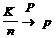 при n ® ¥ или
при n ® ¥ или 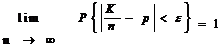 для любого e > 0.
для любого e > 0.
3 Пусть СВ Xi подчиняется закону распределения Бернулли, следовательно M[Xi] = p и D[Xi] = p×q. Так как 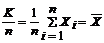 , тогда из следствия теоремы получаем для любого e > 0
, тогда из следствия теоремы получаем для любого e > 0
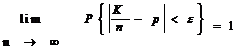 или
или 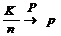 при n ® ¥, что и требовалось показать. 4
при n ® ¥, что и требовалось показать. 4
Задача 1. Пусть СВ X подчиняется закону Ex(1). С помощью неравенств Чебышева оценить вероятности
P{ôX - M[X]ô < a× 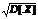 } для a = 1, 2, 3. Сравнить эти оценки с точными значениями.
} для a = 1, 2, 3. Сравнить эти оценки с точными значениями.
Точечные оценки параметров
Статистикой называется любая функция выборочных значений x1, x2, ... xn: G = G(x1, x2, ... xn).
Точечной оценкой Q неизвестного параметра J называется любая статистика G = G(X1, X2, ... Xn), распределение которой сосредоточено вблизи неизвестного значения J. Критерии качества оценок:
Несмещенность. Оценка Q называется несмещенной оценкой J, если M[Q] = J.
Состоятельность. Оценка Q называется состоятельной, если она становится все более точной с ростом объема выборки n, т.е.:
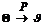 при n ® ¥ или для любого e > 0
при n ® ¥ или для любого e > 0 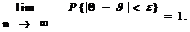
Эффективность. Оценка Q называется эффективной среди оценок Qi, если ее дисперсия является наименьшей среди всех дисперсий этих оценок Qi.
Точечные оценки M[X], D[X] и их свойства
Утверждение 1. Точечная оценка 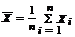 параметра M[X], является несмещенной, состоятельной и эффективной в классе всех линейных оценок вида:
параметра M[X], является несмещенной, состоятельной и эффективной в классе всех линейных оценок вида: 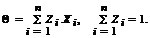
3 Так как Xi являются независимыми СВ, закон распределения которых совпадает с законом распределения СВ X, т.е. M[X] = M[Xi], D[X] = D[Xi]. Тогда, используя свойства математического ожидания и дисперсии имеем:
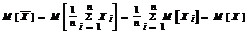 , т.е. несмещенность доказана.
, т.е. несмещенность доказана.
Из следствия закона больших чисел в форме Чебышева очевидно, что 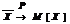 при n ® ¥ или для любого e > 0 справедливо
при n ® ¥ или для любого e > 0 справедливо
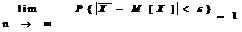 , т.е. состоятельность оценки доказана.
, т.е. состоятельность оценки доказана.
Покажем, что точечная оценка является эффективной в классе всех линейных оценок вида: 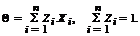
Имеем 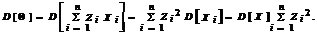 Определим значения Zi, при которых функция
Определим значения Zi, при которых функция 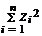 принимает минимальное значение при условии
принимает минимальное значение при условии 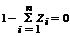 . Для нахождения условного экстремума составим функцию Лагранжа
. Для нахождения условного экстремума составим функцию Лагранжа
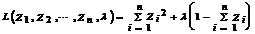 ,
,
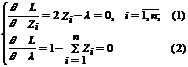 | тогда необходимые условия минимума функции Лагранжа определяет система из уравнений (1) и (2). Из уравнения (1) для i = 1,2, ..., n получаем Zi = l/2. Из уравнения (2) следует l = 2/n. Тогда Zi = 1/n для i = 1,2, ..., n, что и требовалось показать. 4 |
Утверждение 2. Точечная оценка 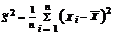 параметра D[X], является смещенной так как
параметра D[X], является смещенной так как 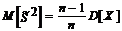 .
.
Утверждение 3. Точечная оценка 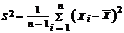 параметра D[X], является несмещенной, состоятельной и эффективной в классе всех квадратичных оценок вида:
параметра D[X], является несмещенной, состоятельной и эффективной в классе всех квадратичных оценок вида: 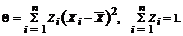
T - распределение Стьюдента
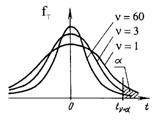 Свойство симметрии: -tn, 1-a= tn, a. Свойство симметрии: -tn, 1-a= tn, a. | Пусть СВ V ~ N(0, 1), а независимая от нее СВ X ~ cn2, тогда СВ 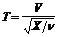 подчиняется t - распределению Стьюдента с n степенями свободы, т.е.: T ~ tn. С ростом n распределение Стьюдента приближается к нормированному нормальному распределению N(0, 1). Уже для n ³ 60 распределение Стьюдента с высокой степенью точности аппроксимируется нормированным нормальным распределением. подчиняется t - распределению Стьюдента с n степенями свободы, т.е.: T ~ tn. С ростом n распределение Стьюдента приближается к нормированному нормальному распределению N(0, 1). Уже для n ³ 60 распределение Стьюдента с высокой степенью точности аппроксимируется нормированным нормальным распределением. |
Таблица 3.
Значения tn, a в зависимости от числа степеней свободы n и вероятности a:
P{ T > tn,a } = a.
| число степеней свободы | Вероятность a: | |||||||
| n | 0,20 | 0,10 | 0,05 | 0,025 | 0,01 | 0,005 | 0,001 | 0,0005 |
| 1,38 | 3,08 | 6,31 | 12,71 | 31,82 | 63,66 | 318,31 | 636,62 | |
| 1,06 | 1,89 | 2,92 | 4,30 | 6,97 | 9,93 | 22,33 | 31,60 | |
| 0,98 | 1,64 | 2,35 | 3,18 | 4,54 | 5,84 | 10,21 | 12,94 | |
| 0,94 | 1,53 | 2,13 | 2,78 | 3,75 | 4,60 | 7,17 | 8,61 | |
| 0,92 | 1,48 | 2,02 | 2,57 | 3,37 | 4,03 | 5,89 | 6,86 | |
| 0,91 | 1,44 | 1,94 | 2,45 | 3,14 | 3,71 | 5,21 | 5,96 | |
| 0,90 | 1,42 | 1,90 | 2,37 | 3,00 | 3,50 | 4,78 | 5,41 | |
| 0,89 | 1,40 | 1,86 | 2,31 | 2,90 | 3,36 | 4,50 | 5,04 | |
| 0,88 | 1,38 | 1,83 | 2,26 | 2,82 | 3,25 | 4,30 | 4,78 | |
| 0,88 | 1,37 | 1,81 | 2,23 | 2,76 | 3,17 | 4,14 | 4,59 | |
| 0,88 | 1,36 | 1,80 | 2,20 | 2,72 | 3,11 | 4,02 | 4,44 | |
| 0,87 | 1,36 | 1,78 | 2,18 | 2,68 | 3,06 | 3,93 | 4,32 | |
| 0,87 | 1,35 | 1,77 | 2,16 | 2,65 | 3,01 | 3,85 | 4,22 | |
| 0,87 | 1,34 | 1,76 | 2,15 | 2,62 | 2,98 | 3,79 | 4,14 | |
| 0,87 | 1,34 | 1,75 | 2,13 | 2,60 | 2,95 | 3,73 | 4,07 | |
| 0,86 | 1,34 | 1,75 | 2,12 | 2,58 | 2,92 | 3,69 | 4,02 | |
| 0,86 | 1,33 | 1,74 | 2,11 | 2,57 | 2,90 | 3,65 | 3,97 | |
| 0,86 | 1,33 | 1,73 | 2,10 | 2,55 | 2,88 | 3,61 | 3,92 | |
| 0,86 | 1,33 | 1,73 | 2,09 | 2,54 | 2,86 | 3,58 | 3,88 | |
| 0,86 | 1,33 | 1,73 | 2,09 | 2,53 | 2,85 | 3,55 | 3,85 | |
| 0,86 | 1 ,32 | 1,72 | 2,08 | 2,52 | 2,83 | 3,53 | 3,82 | |
| 0,86 | 1,32 | 1,72 | 2,07 | 2,51 | 2,82 | 3,50 | 3.79 | |
| 0,86 | 1,32 | 1,71 | 2,07 | 2,50 | 2,81 | 3,48 | 3,77 | |
| 0,86 | 1,32 | 1,71 | 2,06 | 2,49 | 2,80 | 3,47 | 3,75 | |
| 0,86 | 1,32 | 1,71 | 2,06 | 2,48 | 2,79 | 3,45 | 3,73 | |
| 0,85 | 1,31 | 1,70 | 2,04 | 2,46 | 2,75 | 3,39 | 3,65 | |
| 0,85 | 1,30 | 1,68 | 2,02 | 2,42 | 2,70 | 3,31 | 3,55 | |
| 0,85 | 1,30 | 1,67 | 2,00 | 2,39 | 2,66 | 3,23 | 3,46 | |
| 0,84 | 1,29 | 1,66 | 1,98 | 2,36 | 2,62 | 3,16 | 3,37 | |
| ¥ | 0,84 | 1,28 | 1,64 | 1,96 | 2,33 | 2,58 | 3,09 | 3,29 |
F - распределение Фишера
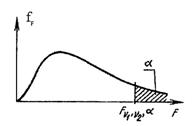 | Пусть СВ X1 ~ cn12, а независимая от нее СВ X2 ~ cn22, тогда СВ 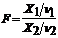 подчиняется F - распределению Фишера с n1 и n2 степенями свободы, т.е.: F ~ Fn1,n2. В таблице 4 приведены значения лишь для a = 0,05, однако, ее можно использовать и при a = 0,95, поскольку Fn1,n2, 1-a = 1/Fn2,n1, a. подчиняется F - распределению Фишера с n1 и n2 степенями свободы, т.е.: F ~ Fn1,n2. В таблице 4 приведены значения лишь для a = 0,05, однако, ее можно использовать и при a = 0,95, поскольку Fn1,n2, 1-a = 1/Fn2,n1, a. |
Таблица 4.
Значения Fn1,n2, a в зависимости от
числа степеней свободы n1, n2 и вероятности a = 0,05: P{ F > Fn1,n2, a } = a.
 n1 n2 n1 n2 | |||||||||
| 18,5 | 19,0 | 19,2 | 19,2 | 19,3 | 19,3 | 19,4 | 19,4 | 19,4 | |
| 10,1 | 9,55 | 9,28 | 9,12 | 9,01 | 8,94 | 8,89 | 8,85 | 8,81 | |
| 7,71 | 6,94 | 6,59 | 6,39 | 6,26 | 6,16 | 6,09 | 6,04 | 6,00 | |
| 6,61 | 5,79 | 5,41 | 5,19 | 5,05 | 4,95 | 4,88 | 4,82 | 4,77 | |
| 5,99 | 5,14 | 4,76 | 4,53 | 4,39 | 4,28 | 4,21 | 4,15 | 4,10 | |
| 5,59 | 4,74 | 4,35 | 4,12 | 3,97 | 3,87 | 3,79 | 3,73 | 3,68 | |
| 5,32 | 4,46 | 4,07 | 3,84 | 3,69 | 3,58 | 3,50 | 3,44 | 3,39 | |
| 5,12 | 4,26 | 3,86 | 3,63 | 3,48 | 3,37 | 3,29 | 3,23 | 3,18 | |
| 4,96 | 4,10 | 3,71 | 3,48 | 3,33 | 3,22 | 3,14 | 3,07 | 3,02 | |
| 4,84 | 3,98 | 3,59 | 3,36 | 3,20 | 3,09 | 3,01 | 2,95 | 2,90 | |
| 4,75 | 3,88 | 3,49 | 3,26 | 3,11 | 3,00 | 2,91 | 2,85 | 2,80 | |
| 4,67 | 3,80 | 3,41 | 3,18 | 3,03 | 2,92 | 2,83 | 2,77 | 2,71 | |
| 4,60 | 3,74 | 3,34 | 3,11 | 2,96 | 2,85 | 2,76 | 2,70 | 2,65 | |
| 4,54 | 3,68 | 3,29 | 3,06 | 2,90 | 2,79 | 2,71 | 2,64 | 2,59 | |
| 4,49 | 3,63 | 3,24 | 3,01 | 2,85 | 2,74 | 2,66 | 2,59 | 2,54 | |
| 4,45 | 3,59 | 3,20 | 2,96 | 2,81 | 2,70 | 2,61 | 2,55 | 2,49 | |
| 4,41 | 3,55 | 3,16 | 2,93 | 2,77 | 2,66 | 2,58 | 2,51 | 2,46 | |
| 4,38 | 3,52 | 3,13 | 2,90 | 2,74 | 2,63 | 2,54 | 2,48 | 2,42 | |
| 4,35 | 3,49 | 3,10 | 2,87 | 2,71 | 2,60 | 2,51 | 2,45 | 2,39 | |
| 4,32 | 3,47 | 3,07 | 2,84 | 2,68 | 2,57 | 2,49 | 2,42 | 2,37 | |
| 4,30 | 3,44 | 3,05 | 2,82 | 2,66 | 2,55 | 2,46 | 2,40 | 2,34 | |
| 4,28 | 3,42 | 3,03 | 2,80 | 2,64 | 2,53 | 2,44 | 2,37 | 2,32 | |
| 4,26 | 3,40 | 3,01 | 2,78 | 2,62 | 2,51 | 2,42 | 2,36 | 2,30 | |
| 4,24 | 3,38 | 2,99 | 2,76 | 2,60 | 2,49 | 2,40 | 2,34 | 2,28 | |
| 4,23 | 3,37 | 2,98 | 2,74 | 2,59 | 2,47 | 2,39 | 2,32 | 2,27 | |
| 4,21 | 3,35 | 2,96 | 2,73 | 2,57 | 2,46 | 2,37 | 2,31 | 2,25 | |
| 4,20 | 3,34 | 2,95 | 2,71 | 2,56 | 2,45 | 2,36 | 2,29 | 2,24 | |
| 4,18 | 3,33 | 2,93 | 2,70 | 2,55 | 2,43 | 2,35 | 2,28 | 2,22 | |
| 4,17 | 3,32 | 2,92 | 2,69 | 2,53 | 2,42 | 2,33 | 2,27 | 2,21 | |
| 4,08 | 3,23 | 2,84 | 2,61 | 2,45 | 2,34 | 2,25 | 2,18 | 2,12 | |
| 4,00 | 3,15 | 2,76 | 2,53 | 2,37 | 2,25 | 2,17 | 2,10 | 2,04 | |
| 3,92 | 3,07 | 2,68 | 2,45 | 2,29 | 2,17 | 2,09 | 2,02 | 1,96 | |
| ¥ | 3,84 | 3,00 | 2,60 | 2,37 | 2,21 | 2,10 | 2,01 | 1,94 | 1,88 |
 n1 n2 n1 n2 | ¥ | |||||||||
| 19,4 | 19,4 | 19,4 | 19,4 | 19,5 | 19,5 | 19,5 | 19,5 | 19,5 | 19,5 | |
| 8,79 | 8,74 | 8,70 | 8,66 | 8,64 | 8,62 | 8,59 | 8,57 | 8,55 | 8,53 | |
| 5,96 | 5,91 | 5,86 | 5,80 | 5,77 | 5,75 | 5,72 | 5,69 | 5,66 | 5,63 | |
| 4,74 | 4,68 | 4,62 | 4,56 | 4,53 | 4,50 | 4,46 | 4,43 | 4,40 | 4,36 | |
| 4,06 | 4,00 | 3,94 | 3,87 | 3,84 | 3,81 | 3,77 | 3,74 | 3,70 | 3,67 | |
| 3,64 | 3,57 | 3,51 | 3,44 | 3,41 | 3,38 | 3,34 | 3,30 | 3,27 | 3,23 | |
| 3,35 | 3,28 | 3,22 | 3,15 | 3,12 | 3,08 | 3,04 | 3,01 | 2,97 | 2,93 | |
| 3,14 | 3,07 | 3,01 | 2,94 | 2,90 | 2,86 | 2,83 | 2,79 | 2,75 | 2,71 | |
| 2,98 | 2,91 | 2,85 | 2,77 | 2,74 | 2,70 | 2,66 | 2,62 | 2,58 | 2,54 | |
| 2,85 | 2,79 | 2,72 | 2,65 | 2,61 | 2,57 | 2,53 | 2,49 | 2,45 | 2,40 | |
| 2,75 | 2,69 | 2,62 | 2,54 | 2,51 | 2,47 | 2,43 | 2,38 | 2,34 | 2,30 | |
| 2,67 | 2,60 | 2,53 | 2,46 | 2,42 | 2,38 | 2,34 | 2,30 | 2,25 | 2,21 | |
| 2,60 | 2,53 | 2,46 | 2,39 | 2,35 | 2,31 | 2,27 | 2,22 | 2,18 | 2,13 | |
| 2,54 | 2,48 | 2,40 | 2,33 | 2,29 | 2,25 | 2,20 | 2,16 | 2,11 | 2,07 | |
| 2,49 | 2,42 | 2,35 | 2,28 | 2,24 | 2,19 | 2,15 | 2,11 | 2,06 | 2,01 | |
| 2,45 | 2,38 | 2,31 | 2,23 | 2,19 | 2,15 | 2,10 | 2,06 | 2,01 | 1,96 | |
| 2,41 | 2,34 | 2,27 | 2,19 | 2,15 | 2,11 | 2,06 | 2,02 | 1,97 | 1,92 | |
| 2,38 | 2,31 | 2,23 | 2,16 | 2,11 | 2,07 | 2,03 | 1,98 | 1,93 | 1,88 | |
| 2,35 | 2,28 | 2,20 | 2,12 | 2,08 | 2,04 | 1,99 | 1,95 | 1,90 | 1,84 | |
| 2,32 | 2,25 | 2,18 | 2,10 | 2,05 | 2,01 | 1,96 | 1,92 | 1,87 | 1,81 | |
| 2,30 | 2,23 | 2,15 | 2,07 | 2,03 | 1,98 | 1,94 | 1,89 | 1,84 | 1,78 | |
| 2,27 | 2,20 | 2,13 | 2,05 | 2,01 | 1,96 | 1,91 | 1,86 | 1,81 | 1,76 | |
| 2,25 | 2,18 | 2,11 | 2,03 | 1,98 | 1,94 | 1,89 | 1,84 | 1,79 | 1,73 | |
| 2,24 | 2,16 | 2,09 | 2,01 | 1,96 | 1,92 | 1,87 | 1,82 | 1,77 | 1,71 | |
| 2,22 | 2,15 | 2,07 | 1,99 | 1,95 | 1,90 | 1,85 | 1,80 | 1,75 | 1,69 | |
| 2,20 | 2,13 | 2,06 | 1,97 | 1,93 | 1,88 | 1,84 | 1,79 | 1,73 | 1,67 | |
| 2,19 | 2,12 | 2,04 | 1,96 | 1,91 | 1,87 | 1,82 | 1,77 | 1,71 | 1,65 | |
| 2,18 | 2,10 | 2,03 | 1,94 | 1,90 | 1,85 | 1,81 | 1,75 | 1,70 | 1,64 | |
| 2,16 | 2,09 | 2,01 | 1,93 | 1,89 | 1,84 | 1,79 | 1,74 | 1,68 | 1,62 | |
| 2,08 | 2,00 | 1,92 | 1,84 | 1,79 | 1,74 | 1,69 | 1,64 | 1,58 | 1,51 | |
| 1,99 | 1,92 | 1,84 | 1,75 | 1,70 | 1,65 | 1,59 | 1,53 | 1,47 | 1,39 | |
| 1,91 | 1,83 | 1,75 | 1,66 | 1,61 | 1,55 | 1,50 | 1,43 | 1,35 | 1,25 | |
| ¥ | 1,83 | 1,75 | 1,67 | 1,57 | 1,52 | 1,46 | 1,39 | 1,32 | 1,22 | 1,00 |
Таблица 5.
Нормальных распределений
| № п/п | Параметр | Информация о других параметрах распределения | Доверительный интервал параметра с доверительной вероятностью g |
| 1. | mX | sX известно | 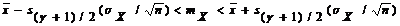 |
| 2. | mX | sX неизвестно | 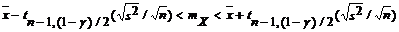 |
| 3. | s2X | mX известно | 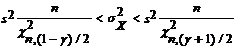 |
| 4. | s2X | mX неизвестно | 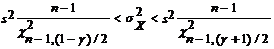 |
| 5. | sX | mX неизвестно | 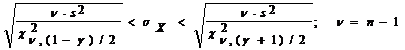 |
| 6. | 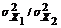 | 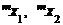 неизвестны неизвестны | 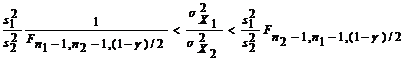 |
| 7. | r | 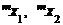 и и 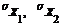 неизвестны неизвестны | 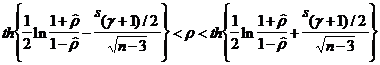 это справедливо для достаточно больших n (n > 10) это справедливо для достаточно больших n (n > 10) |
____________
Примечание:
| n - | объем выборки x1, x2, ... xn; | |
| sp - | квантиль уровня p нормированного нормального распределения; | (см. таблицу 1) |
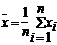 - - | выборочное среднее; | |
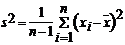 - - | выборочное значение дисперсии СВ X; | |
| r - | коэффициент корреляции СВ X1 и X2; | |
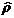 - - | выборочный коэффициент корреляции СВ X1 и X2; | |
| c2n, a - | значение распределения Пирсона; | (см. таблицу 2) |
| tn, a - | значение t - распределения Стьюдента; | (см. таблицу 3) |
| Fn1,n2, a - | значение F - распределения Фишера. | (см. таблицу 4) |
Правило произведения
Если первое событие может произойти n1 способами, а второе - n2 способами независимо от первого, то совместная реализация может произойти n1×n2 способами.
Правило суммы
Если первое событие может произойти n1 способами, а второе - n2 способами независимо от первого, то первое или второе события могут произойти n1+n2 способами.
Комбинаторный метод вычисления вероятностей
При подсчете числа элементарных исходов, составляющих события в классической схеме, часто используются известные формулы комбинаторики. Каждая из комбинаторных формул определяет общее число элементарных исходов в некотором идеализированном эксперименте по выбору наудачу m элементов из n различных элементов исходного множества E = {e1, e2, ..., en}.
При постановке каждого такого эксперимента строго оговорено, каким способом производится выбор и что понимается под различными выборками. Существуют две принципиально отличные схемы выбора: в первой схеме выбор осуществляется без возвращения элементов (это значит, что отбираются либо сразу все m элементов, либо последовательно по одному элементу, причем каждый отобранный элемент исключается из исходного множества). Во второй схеме выбор осуществляется поэлементно с обязательным возвращением отобранного элемента на каждом шаге и тщательным перемешиванием исходного множества перед следующим выбором. После того, как выбор тем или иным способом осуществлен, отобранные элементы (или их номера) могут быть либо упорядочены (т.е. выложены в последовательную цепочку), либо нет. В результате получаются следующие четыре различные постановки эксперимента по выбору наудачу m элементов из общего числа n различных элементов множества Е.
