Множественное линейное уравнение регрессии

Пусть требуется построить линейную модель зависимости признака Y от набора независимых переменных 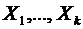. Модель множественной линейной регрессии записывается в виде:

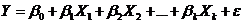, (2.1)

где 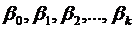– коэффициенты модели, e - случайная величина, удовлетворяющая условиям: математическое ожидание ошибки равно нулю; дисперсия ошибки не зависит от номера наблюдения; ошибки разных наблюдений не зависят друг от друга.

Пусть для оценки неизвестных параметров b_j (j = 1,…k) уравнения регрессии (2.1) взята случайная выборка объемом n и y_i, x_i1,…x_ik – результат i наблюдения, где i=1,…n.

То есть имеется n наблюдений объясняемой переменной 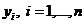, и n наблюдений k объясняющих переменных .

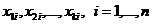В матричной форме линейная модель имеет вид:

Y=Xβ+ε, (2.2)

где 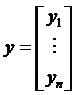- вектор-столбец наблюдений размерности n; 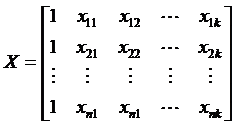- матрица независимых переменных размерности n´(k+1);

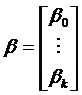- вектор-столбец неизвестных параметров, подлежащих оцениванию, размерности (k+1);

- вектор-столбец случайных ошибок размерности n.

Применяя метод наименьших квадратов, получим вектор оценок коэффициентов модели:

b=(X^TX)^-1X^TY. (2.3)

Тогда выборочное уравнение регрессии имеет вид:

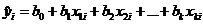. (2.4)

Несмещенную оценку остаточной дисперсии найдем по формуле:

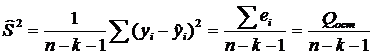. (2.5)

Для проведения регрессионного анализа рассчитывают следующие показатели:

- коэффициент детерминации имеет тот же самый смысл, что и R² для парной регрессии:

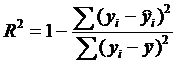; (2.6)

- множественный коэффициент корреляции, являющийся мерой линейной зависимости между переменной у и факторами х₁, х₂,…, x_k:

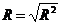; (2.7)

- скорректированный коэффициент детерминации корректирует значение коэффициента R² с учетом числа независимых переменных и размером выборки, чтобы снизить влияние количества переменных:

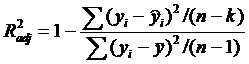; (2.8)

- стандартная ошибка представляет собой стандартное отклонение для остатков. Измеряет рассеивание значений у относительно регрессии:

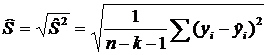. (2.9)

Для проверки значимости уравнения регрессии находят:

- общую сумму квадратов, которая объясняет общую изменчивость:

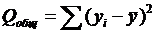; (2.10)

- сумму квадратов остатков – это часть дисперсии, не объясненная линейной зависимостью:

Q_ост = 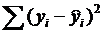; (2.11)

- сумму квадратов, обусловленных регрессией, которая измеряет часть дисперсии, объясняемую регрессионной зависимостью:

Q_регр = 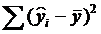. (2.12)

Выполняется условие:

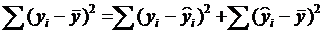, то есть

Qобщ =	Qрегр +	Qост. (2.13)
Общая изменчивость у	Изменчивость, объясненная линейной зависимостью	Остаточная или необъясненная изменчивость

Для оценки значимости уравнения регрессии, то есть проверки гипотезы H₀: β₁= β₂=…= β_k=0 рассчитывают статистику:

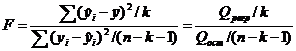, (2.14)

имеющую распределение Фишера-Снедекора (F-распределение).

По таблице F-распределения находят критическое значение F_кр(a; ν₁,ν₂), где a- уровень значимости; ν₁, ν₂ - число степеней свободы, ν₁=k, ν₂=n-k-1. Если выполняется F_набл > F_кр, то гипотеза отвергается и уравнение считается значимым.

Значимость коэффициентов регрессии β_j проверяется с помощью t-критерия. Рассчитывают статистику:

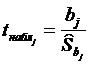, (2.15)

где 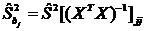- дисперсия коэффициента регрессии b_j;

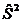- несмещенная оценка остаточной дисперсии (2.5);

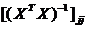- элементы обратной матрицы, стоящие на главной диагонали;

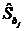- стандартная ошибка коэффициента b_j. Измеряет отклонение имеющихся данных у_i от их оценок .

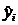Из таблиц распределения Стьюдента (t-распределения) находят критическое значение t_кр(α; ν=n-k-1), где ν - число степеней свободы.

Если |t_набл|>t_кр, то гипотеза H₀: β_j=0 отвергается и коэффициент считается значимым. Если |t_набл| 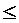t_кр, то гипотеза H₀ не отвергается.

Доверительные интервалы для значимых коэффициентов регрессии строятся по формуле:

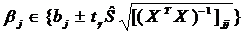, (2.16)

где t_γ определяется из таблицы распределения Стьюдента для уровня значимости α=1-γ и числа степеней свободы ν=n-k-1.

Задача 2

Имеются данные о зависимости прибыли у (тыс. руб) от расходов на рекламу (тыс. руб) х₁ и стоимости основных фондов х₂ (тыс. руб) Данные приведены в таблице 2.1.

На основании данных таблицы:

а) построить уравнение регрессии у = b₀+ b₁х₁ +b₂х₂ + e;

б) найти оценку и проверить на 5% уровне значимость уравнения регрессии, то есть гипотезу Н₀: β₁= β₂=0;

в) проверить значимость каждого коэффициента регрессии;

г) Найти коэффициент детерминации R².

Таблица 2.1

x1
x2	6,2	5,2	6,5	6,9	10,2	15,5	17,2	16,2	20,5	16,9	18,2	19,5	26,2	35,2	26,5	26,9	30,2	35,5	40,0	35,0
y

Решение

Решим задачу в программе Exel с помощью пакета «Анализ данных».

Для проведения регрессионного анализа на панели инструментов выберите «Сервис», затем «Надстройки» и при появлении окна поставить флажок на «Пакет анализа», нажать ОК.

Для решения задачи введем данные задачи в столбцы А, В и С (рис.2.1).

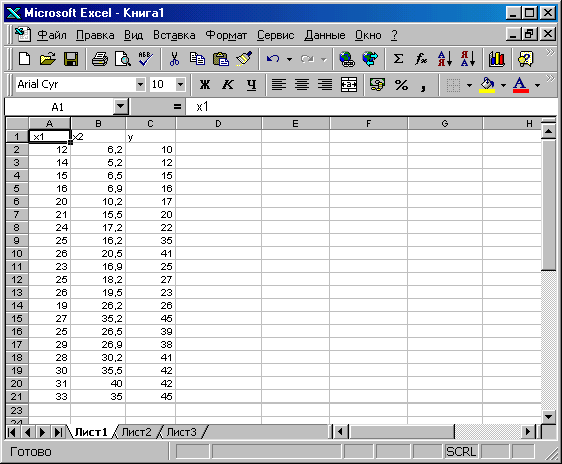
Рис. 2.1. Входные данные

Выберите еще раз «Сервис» и «Анализ данных». При появлении окна «Анализ данных» - нажмите курсором на инструмент анализа: «Регрессия» (см. рис. 2.2).

После выбора «Регрессии» появляется окно «Регрессия» (см. рис. 2.3).

Рис. 2.2. Окно «Анализ данных»

Рис. 2.3. Окно «Регрессия»

В категории Входные данные окна «Регрессия» необходимо указать:

- Входной интервал Y– диапазон зависимых переменных, состоящих из одного столбца;

- Входной интервал Х- диапазон независимых переменных, подлежащих анализу. Может состоять из одного или более столбцов. Максимальное количество столбцов равно 16;

- Константа-ноль – для построения регрессии без свободного члена (b₀), то поставьте флажок в этом окне;

- Уровень надежности – для включения дополнительного уровня надежности, установите флажок в соответствующем окне. По умолчанию уровень надежности равен 95%;

- Остатки(остатки, стандартизированные остатки, график остатков и график подбора) – используются как дополнительный анализ параметров вывода.

Укажем курсором столбцы входных данных (см. рис. 2.4). Выбор столбцов проводится курсором.

Входной интервал Y – это столбец С2 – С45.

Входной интервал Х – это два столбца А2 до В21.

Необходимо заполнить Параметры вывода: можно установить Выходной интервал, то есть указать ячейку, в которой появится результат. Если выходной интервал не устанавливать, то решение появится на новом листе Exel.

Рис. 2.4. Выбор диапазона регрессии

Нажав ОК, получим результаты решения задачи (см. рис. 2.5).

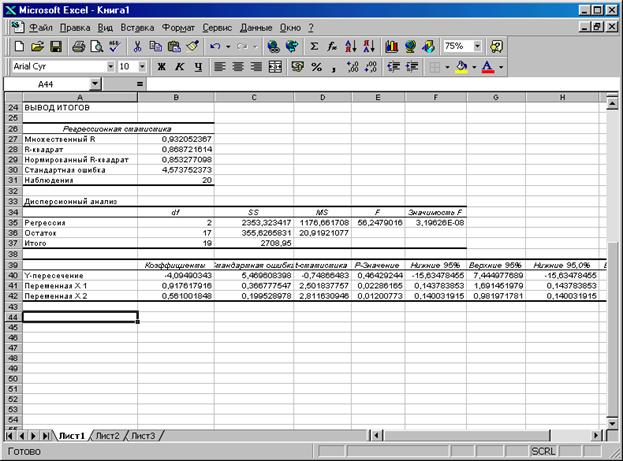
Рис. 2.5. Вывод итогов построения регрессии

В столбце «Коэффициенты» получены коэффициенты уравнения регрессии.

Коэффициент b₀= - 4,09 в Таблице анализа – это Y-пересечение.

Таким образом, получили уравнение регрессии:

.

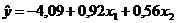Коэффициент b₁=0,92 показывает, что при увеличении расходов на рекламу на 1 тыс. руб. прибыль увеличивается в среднем на 0,92 тыс. руб., а увеличение стоимости основных фондов на 1 тыс. руб. приводит к увеличению прибыли в среднем на 0,56 тыс. руб.

Стандартные ошибки коэффициентов:

,

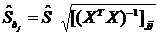где 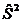- стандартная ошибка (2.9);

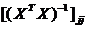- элементы обратной матрицы, стоящие на главной диагонали.

Они составляют: .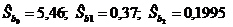

Для проверки значимости коэффициентов регрессии рассчитываются t –статистики по формуле (2.15).

Получены следующие t-статистики (рис. 2.5):

; ; .

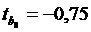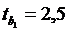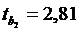Находим критическое значение распределения Стьюдента для вероятности (уровня значимости) 0,05 и число степеней свободы n = n-k-1=20-2-1=17.

Критическое значение находим из таблиц распределения Стьюдента или с помощью статистической функции СТЮДРАСПОБР(0,05;17) = 2,11.

Для проверки гипотезы H₀: β_j=0 сравниваем полученные значения для всех коэффициентов t_набл с t_кр=2,11. Получим, что все коэффициенты значимы, кроме b₀. То есть на прибыль значимо оказывают влияние расходы на рекламу и стоимость основных фондов.

Для проверки значимости коэффициентов можно использовать Р-значения (ячейки Е40-Е42).

По величине Р-значения возможно определять значимость коэффициентов, не находя критическое значение t-статистики. Если значение t-статистики велико, то соответствующее значение вероятности значимости мало – меньше 0,05, и можно считать, что коэффициент регрессии значим. И наоборот, если значение t-статистики мало, соответственно вероятность значимости больше 0,05 – коэффициент считается незначимым.

Для коэффициентов b₁ значения вероятности близко к нулю (0,02), следовательно, коэффициент b₁ можно считать значимым. Аналогично определяется значимость коэффициента b₂.

Далее на рис. 2.5 представлены доверительные интервалы (нижняя и верхняя границы), рассчитываемые по формуле (2.15).

В разделе Регрессионная статистика получили:

- коэффициент детерминации R²=0,98, рассчитывается по формуле (2.6), и показывает, что модель достаточно хорошо описывает данные, так как R² близок к 1;

- скорректированный коэффициент детерминации имеет тот же смысл, что и R², но считается, что он точнееотражает степень адекватности модели;

- стандартная ошибка, рассчитываемая по формуле (2.9).

В Дисперсионном анализе вычисляются:

- df – число степеней свободы;

- SS – суммы квадратов разностей;

- МS - оценки дисперсий;

- F – вычисленное значение критерия Фишера;

- Значимость F.

Сумма квадратов регрессии вычисляется по формуле (2.12):

Q_регр = 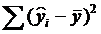= SS₁;

- сумма квадратов остатков:

Q_ост = 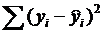= SS₂;

- общая сумма квадратов:

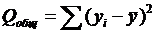=SS.

Выполняется условие (2.13):

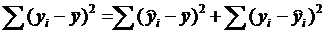= SS₁+SS₂=SS.

То есть 2353,32+355,62=2706,95.

Число степеней свободы df для SS₁ равно df₁=2 (k - число независимых переменных или факторов), для SS₂: df₂ = n – k – 1= 20 – 2 –1 =17, для SS: df = n – 1= 20 – 1 =19.

Получены оценки средних кавдратов:

;

;

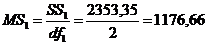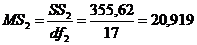наблюдаемое значение F-критерия (2.14):

.

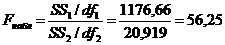Сравним полученное значение F_набл с критическим. Так как F_крит=3,59<F_набл=3,59, то гипотеза Н₀: β₁= β₂=0 отвергается и уравнение считается значимым.

Значимость F – это вероятность значимости для F критерия. В нашем случае она фактически равна нулю (3,19Е-8=3,19·10^-8=0), то есть гипотеза H₀: β₁= β₂=0 отвергается и уравнение считается значимым.