Влияние инерционности элементов системы на процессы поиска экстремума

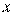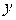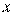До сих пор мы не обращали внимания на динамические свойства объектов управления. Предполагалось, что изменение входного сигнала объекта вызывает мгновенное изменение выходного сигнала по статической характеристике объекта . Однако подавляющее большинство объектов регулирования обладает инерцией, т.е. после изменения выходной сигнал объекта 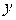изменяется не мгновенно. Эта зависимость, как мы знаем, обычно описывается системой дифференциальных уравнений. Соответственно меняется динамика всей экстремальной системы.

Как уже отмечалось, наиболее широко распространенными методами анализа динамики ЭС является использование методов временных диаграмм на фазовой плоскости (графические методы) и методы гармонической линеаризации. Рассмотрим применение метода фазовой плоскости для исследования ЭС с инерционными объектами.

При рассмотрении систем ЭР объектов в большинстве случаев удобно представить последовательным соединением трех звеньев, как это показано на рис. 3.5, где

- входное линейное звено,

- экстремальная нелинейная статическая характеристика,

- выходное линейное звено.

Рис. 3.5. Структура инерционного экстремального объекта

В соответствии с приведенной схемой рассмотрим систему с запоминанием экстремума, приведенную на рис. 3.6.

Рис.3.6. Система с запоминанием экстремума для инерционного объекта

Будем считать, что исполнительное устройство работает релейно. Реверс происходит в моменты, когда . Будем изображать процессы в фазовой плоскости .

Уравнения движения системы имеют вид:

- уравнение динамической части объекта, (3.1)

- уравнение исполнительного органа. (3.2)

В соответствии с выражениями (3.1, 3.2 ) можно вычертить фазовые траектории системы или временные диаграммы. Начнем с последних (с точки зрения простоты понимания).

Пусть в момент система находится в точке , где и . (рис. 3.7)

Рис.3.7 Начальный этап движения инерционного объекта

В некоторый момент включился экстремальный регулятор и начал перемещать исполняющий механизм в сторону увеличения 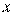. Т.к. , берем знак + в уравнении (3.2).

В силу инерционности система не может двигаться по статической характеристике и сигнал на выходе 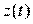отличается от 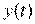. Характер траектории зависит от инерционности объекта, определяемой постоянной времени , а также скорости изменения входного сигнала. Для объекта с меньшей (или при меньшей скорости изменения сигнала на входе) кривая будет лежать выше, чем кривая и наоборот.

Более интегрированные временные диаграммы движения инерционного объекта приведены на рис. 3.8.

Рис.3.8. Переходный процесс в ЭС с инерционным объектом

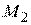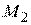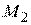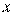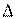До точки знак и возрастет. В точке , которая находится на статической характеристике, разность , и равны нулю. В точке достигнут максимум . При дальнейшем увеличении знак разности в квадратной скобке меняется , производная . В точке разность между и достигает порога , происходит реверс исполнительного механизма и координата 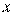начинает уменьшаться. Из-за инерции объекта выходной сигнал некоторое время уменьшается, т.к. . В точке производная , а затем начинает увеличиваться и т.д. Через некоторое время в системе устанавливается периодический режим колебаний вокруг экстремума (рис.3.9).

Рис.3.9. Установившийся процесс в ЭС с инерционным объектом

В рассмотренном случае мы пользовались для построения переходного процесса в системе уравнениями (3.1), (3.2) для производных по времени и получили временные диаграммы изменения . Аналогичным образом можно построить фазовый портрет системы. Для этого на основе уравнений (3.1) и (3.2) составим уравнение движения системы в фазовой плоскости. Разделив уравнение (3.1) на уравнение (3.2) получаем дифференциальное уравнение в фазовом пространстве

, где . (3.3)

На рис. 3.10а представлен фазовый портрет движения объекта. Рис.3.10б иллюстрирует начальный этап процесса

Рис.3.10 Фазовый портрет движения инерционного объекта

Пусть регулятор включился в работу в точке 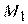при . Причем, пусть исполнительное устройство уменьшает выходной сигнал. При этом уравнение нужно взять со знаком минус.

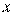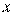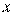В правой части уравнения также будет знак минус, однако , поэтому и уменьшению соответствует уменьшение . В точке произойдет реверс ИУ и начнет возрастать. При этом в правой части уравнения будет плюс (от управления), но т.к , то и возрастанию отвечает уменьшение до точки , где . .

Далее возрастает вместе с 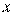до точки . Здесь и далее меняет знак на минус. В точке происходит реверс, меняется знак правой части уравнения , но т.к. 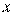уже меняется в другую сторону, то попрежнему убывает. Наконец, в точке меняет знак скобка и начинает снова возрастать и так до установления режима периодических колебаний. Этот режим изображается петлей “восьмеркой” с параметрами , причем , т.е. петля симметрична относительно значения .

Легко видеть что переходный процесс на плоскости с координатами дает ту же информацию о состоянии системы, что и приведенные ранее временные диаграммы, но значительно удобнее, т.к. на одном графике сразу и вход и выход объекта.

Фазовый портрет можно получить сразу из временных диаграмм, если с момента реверса откладывать время в противоположную сторону. Рассмотренная фазовая поверхность ”двуместная “. На каждом листе нанесено движение при одном значении сигнала реле, и листы “склеены”.

Средний уровень значения выходного сигнала при автоколебаниях вокруг экстремума ниже уровня экстремума . Это следствие того, что происходит процесс непрерывного “рыскания“ вокруг . Значение определяется выражением

,

где - функция, описывающая одну ветвь петли автоколебаний (от до ). Разность

,

как обычно, называется потерей на поиск .

Рис.3.11 Установившийся процесс рыскания на фазовом портрете

Потеря на поиск – важный показатель качества ЭС и нужно стремиться к ее снижению. Второй важный показатель – амплитуда автоколебаний на входе. Чем меньше амплитуда автоколебаний на входе, тем меньше 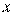отклоняется от и тем лучше работает система. Обычно ее оценивают либо в абсолютных значениях , либо в относительных , относя по всему диапазону изменения 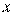.