Математические модели объектов управления с переменными и неопределенными параметрами.

Под объектом управления понимают совокупность технических средств, которая нуждается в оказании специально организованных воздействий извне для достижения поставленной цели управления.

Обычно задача управления объектом ставится следующим образом. Состояние объекта управления (рис. 1.1) характеризуется вектором фазовых координат , составляющие которого могут иметь самую различную физическую природу. К объекту управления приложены внешние воздействия: управляющие воздействия, определяемые вектором и возмущающие воздействия, характеризуемые вектором . Управляющие воздействия – это воздействия, которые могут целенаправленно меняться для достижения поставленной цели управления. Возмущающие воздействия определяют влияние внешней среды и, как правило, мешают достижению цели управления.

Рис. 1.1 Объект управления

Векторы связаны некоторой зависимостью. Нами в дальнейшем будут рассматриваться только такие объекты, в которых связь между составляющими векторов может быть записана в виде обыкновенных дифференциальных уравнений (это так называемые модели макроуровня, или модели систем с сосредоточенными параметрами)

. (1.1)

Здесь функции непрерывны и непрерывно дифференцируемы по совокупности .

Обычно объект управления задан (это означает, что задана система уравнений (1.1) со всеми коэффициентами) и его свойства изменить нельзя.

Управлять объектом – это значит вырабатывать вектор управляющих воздействий с таким расчетом, чтобы состояние объекта управления, определяемое вектором , изменялось по требуемому закону независимо от действия на объект возмущающих воздействий. Закон изменения вектора управляющих воздействий во времени или в зависимости от состояния объекта управления называется алгоритмом управления.

При изучении адаптивных систем будем полагать, что процессы в объекте управления описываются уравнениями

где - вектор состояния объекта управления, - управляющее воздействие, 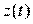- вектор координатных возмущающих воздействий, 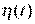- вектор неизвестных параметров (параметрических возмущений), - вектор нелинейных функций, 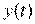- выходная (управляемая) величина. Структурная схема объекта управления, построенная по приведенным уравнениям, показана на рис. 1.2. Особенность приведенных уравнений в учете параметрических возмущений.

При составлении реальных моделей следует учитывать, что сложная математическая модель может создать непреодолимые трудности на этапе анализа и синтеза системы автоматического управления. Поэтому наибольшее распространение получили линейные модели, описываемые уравнениями

Рис. 1.2 Структурная схема объекта управления

Здесь параметрические возмущения включены в коэффициенты уравнений. Значения параметров и законы изменения их во времени зависят от многих факторов. Среди них можно назвать: изменение режима работы объекта управления; старение элементов объекта управления; разброс параметров в пределах технологического допуска и др. Отсутствие информации об этих факторах заставляет считать параметры неопределенными, относится к объектам с неопределенными параметрами.

Иногда объект управления с неопределенными параметрами записывают в виде

При этом неопределенными считаются не параметры объекта, а коэффициенты его математической модели.

Случай, когда о параметрах объекта ничего не известно встречается крайне редко. В большинстве случаев о неопределенных параметрах все-таки имеется некоторая информация. В зависимости от объема и характера этой информации выделяются следующие случаи:

● Параметры объекта управления являются постоянными и принимают произвольные значения в заданных диапазонах ;

● Параметры объекта управления являются постоянными и принимают случайные значения, подчиняясь известному закону распределения с неизвестными параметрами;

● Параметры объекта управления являются постоянными и принимают случайные значения, подчиняясь известному закону распределения с известными параметрами;

● Параметры объекта управления являются функциями времени, удовлетворяющими неравенствам ;

● Параметры объекта управления являются случайными функциями времени с известным законом распределения, но неизвестными параметрами этого распределения;

● Параметры объекта управления являются случайными функциями времени с известным законом распределения, и известными параметрами этого распределения.