Адаптивные системы управления

ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

А.В. Воронин

АДАПТИВНЫЕ СИСТЕМЫ УПРАВЛЕНИЯ

Рекомендовано в качестве учебного пособия
Редакционно-издательским советом
Томского политехнического университета

Издательство

Томского политехнического университета

	УДК 681.3 ББК 32.97
	Воронин А.В. Адаптивные системы управления: учебное пособие / А.В. Воронин: Томский политехнический университет. – Томск: Изд-во Томского политехнического университета, 2014. – 77 с. В авторской редакции

Пособие подготовлено на кафедре интегрированных систем управления и предназначено для студентов ИДО, обучающихся по направлению 220700 «Автоматизация технологических процессов и систем».

УДК 681.3

ББК 32.97

© ФГБОУ ВПО НИ ТПУ, 2014

© Воронин А.В., 2014

© Оформление. Издательство Томского
политехнического университета, 2014

ВВЕДЕНИЕ

Назначение адаптивных систем управления.

Как отмечалось выше, необходимость адаптивного управления возникает, когда недостаточна априорная информация или динамические характеристики объекта в процессе функционирования системы управления изменяются в широких пределах. Такая ситуация возникают во многих производствах.

Аэродинамические характеристики самолетов зависят от скорости и высоты полета, от атмосферных условий, в которых происходит полет. И во время полета отдельные параметры, определяющие динамические свойства самолета, могут изменяться в десятки раз. В этих условиях с задачей качественного управления самолетом обычные автопилоты могут не справиться.

Модели технологических процессов в металлургии, химии, нефтехимии являются сложными. Их параметры и, возможно, структуры из-за недостаточной априорной информации не всегда известны.

Кроме того, эти параметры могут изменяться во время протекания технологического процесса в указанных отраслях. Поэтому обычные системы управления во многих случаях не могут обеспечить качественного, а иногда и просто устойчивого управления такими технологическими процессами [62].

При разработке унифицированных регуляторов для широкого класса объектов параметры регуляторов заранее не могут быть точно рассчитаны и установлены. Достаточно напомнить о том, что процедура линеаризации всегда проводится в некоторой точке и полученный регулятор является работоспособным в малой окрестности точки линеаризации. Поэтому, если эти регуляторы являются неадаптивными, то при их использовании в каждом конкретном случае они требуют настройки. Использование адаптивных регуляторов избавит пользователей от этой процедуры, что позволит сэкономить их время и «силы».

В большинстве случаев адаптивное управление преследует цель нейтрализации параметрической неопределенности или неизбежных изменений параметров объекта. Однако в некоторых случаях, в особенности при управлении технологическим процессами, где могут присутствовать сотни управляющих контуров, адаптивное управление также используется, чтобы уменьшить число конструктивных параметров ручной настройки и тем самым увеличить эффективность и практичность системы управления.

Резюмируя изложенное, можно утверждать, что применение принципов адаптивного управления позволяет [49, 4]:

— обеспечить оптимальный режим работы системы управления в условиях неполной информации;

— обеспечить работоспособность системы управления в условиях изменения динамических свойств объекта в широких пределах;

— создать унифицированные регуляторы для широкого класса объектов;

— снизить технологические требования к изготовлению отдельных узлов и элементов;

— сократить сроки разработки и наладки систем.

Два подхода к синтезу САУ для объектов с

Неопределенными параметрами

В настоящее время в ТАУ существуют два подхода, позволяющие решить задачу управления объектами с переменными и неопределенными параметрами.

Первый подход базируется на использовании регуляторов, алгоритмы работы которых напрямую не зависят от меняющихся или неизвестных параметров. Идея подхода состоит в том, чтобы на этапе синтеза сделать систему максимально нечувствительной к изменяющимся или неопределенным параметрам. В основе подхода лежит свойство обратных связей устранять влияние неопределенностей, либо, по крайней мере, уменьшать это влияние до некоторой величины. Почти любой обычный регулятор, рассчитанный для рабочей точки, благодаря заложенным в нем запасам сохраняет работоспособность и при изменении параметров объекта в некотором диапазоне. Но если не используются специальные методы, этот диапазон оказывается небольшим.

Во многих случаях путем выбора более сложной структуры регулятора удается существенно расширить диапазон изменения параметров, в котором обеспечивает неизменное или малое изменение показателей качества управления. Такие системы, имеющие пониженную чувствительность к изменяющимся параметрам объекта управления, называются грубыми системами. В настоящее время существует несколько подходов к синтезу грубых систем.

Один из них заключается в выборе такой структуры системы, при которой место включения объекта управления соответствует достижению минимальной чувствительности регулируемой переменной к вариациям параметров.

В основу другого подхода положено использование в системе избыточных элементов, представляющих специальные корректирующие устройства, которые рассчитываются так, чтобы снизить чувствительность системы к изменениям параметров объекта управления.

Таким образом, в грубых системах обеспечение требуемого качества управления в условиях меняющихся или неопределенных параметров достигается за счет увеличения объема рабочей (апостериорной) информации. В этих системах при формировании управляющего сигнала кроме информации о регулируемой величине 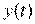используются измерения других, доступных для измерения величин, и эти данные подвергаются преобразованию с помощью более сложных линейных и нелинейных законов. Часто грубые системы называют системами с пассивной адаптацией.

Другой подход связан с разработкой собственно адаптивных систем, реализующих подстройку параметров и\или структуры регулятора под изменяющиеся параметры объекта.

1.6. Структура и типы адаптивных систем управления.

Адаптивные системы управления включают объект, регулятор и адаптор (блок адаптации) (рис.1.3). Объект и регулятор, вырабатывающий управляющее воздействие на объект, образуют основной контур. Регулятор содержит варьируемые параметры. Адаптор на основе обработки доступной ему информации вырабатывает управляющее воздействие, производящее подстройку варьируемых параметров регулятора. Регулятор совместно с адаптором образуют адаптивный регулятор.

Таким образом, адаптивная система обладает способностью «приспосабливаться» к изменениям параметров объекта. В ней автоматически производятся такие же изменеия, какие бы внес проектировщик, если бы имел возможностьполучить дополнительную информацию о поведении системы.

Как видим, адаптивная система управления имеет иерархическую структуру: она имеет, по крайней мере, два уровня. Основной контур образует первый (низший) уровень, а контур, содержащий адаптор и называемый контуром адаптации, — второй уровень.

На нижнем уровне решается обычная задача регулирования. Структура контура регулирования зависит от характера изменения 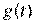. Это могут быть задачи стабилизации, слежения или программного управления. Обычно реализуется принцип регулирования по отклонению или комбинированного управления.

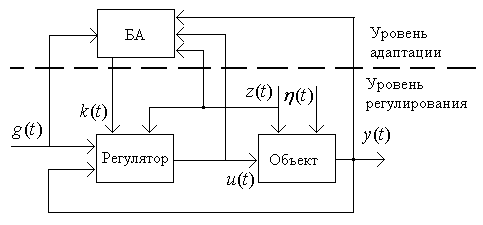
Рис. 1.3 Простейшая блок- схема адаптивной системы

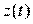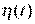Задача верхнего уровня состоит в стабилизации или оптимизации характеристик основного контура системы в условиях изменения и . В качестве объекта управления контура адаптации выступает основной контур системы, при этом управляемой величиной является некоторый показатель, характеризующий динамические свойства основного контура, а управляющим воздействием – вектор 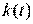параметров регулятора, к которым относятся настраиваемые параметры и параметры, определяющие структуру регулятора.

Задачу стабилизации или поиска экстремума указанного показателя решает блок БА, который работает по измерениям 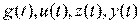, меняя вектор параметров .

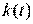В частном случае, адаптация может работать, как и обычная система управления, по разомкнутому, замкнутому и комбинированному принципу.

Следует заметить, что в блок адаптации не заводится информация о параметрических возмущениях. Дело в том, что измерения 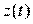и 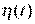это задачи разного уровня сложности. Если 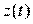часто доступны для измерения (хотя и эта задача может быть весьма непростой), то параметрические возмущения обычно не измеряемы. Их можно оценить только методами идентификации.

В общем случае в АС возможны три и больше уровней. В частности, если для синтеза адаптора в завершенном виде априорной информации недостаточно и, допустим, какие-либо его параметры должны уточняться в процессе функционирования системы, потребуется третий уровень — контур адаптации адаптора. Адаптор выполняет двоякую функцию: изучение объекта и настройку регулятора.

Экстремальные,

самонастраивающиеся (СНС),

самоорганизующиеся (СОС),

Самообучающиеся.

Самые старые и самые простые АС, этоэкстремальные системы. В экстремальных системах обеспечивается оптимальный режим (точнее квазиоптимальный, т.к. обычно ЭС являются поисковыми, а поисковые сигналы возбуждают систему), соответствующий экстремуму статической характеристики объекта при ее «дрейфе», за счет автоматического регулирования сигналов на входе экстремального объекта.

Достоинство такой системы - простота, скромные требования к информации и точное поддержание экстремума. Недостатком является квазиоптимальность и медленность работы при поисковой реализации, требования к наличию у объекта экстремальной характеристики.

К самонастраивающимся системам относятся те адаптивные системы, в которых структура основного регулятора задана и для достижения требуемого качества управления в основном контуре перестраиваются коэффициенты закона управления, реализуемого в регуляторе.

ЭКСТРЕМАЛЬНЫЕ СИСТЕМЫ

Принцип действия ЭС

Как уже отмечалось, в зависимости от количества координат, характеризующих экстремальный статический режим объекта управления, ЭС делят на одномерные и многомерные. Начнем с одномерной ЭС, обобщенная структура которой представлена на рис. 2.9. В основном, ЭС содержит те же обязательные функциональные элементы, что и любая САР.

Рис. 2.9 Структура экстремальной системы

В частности, на рис. 2.9:

ИУ – исполнительное устройство,

УПУ – усилительно-преобразовательное устройство,

ИОЭ – измеритель отклонения от экстремума.

Основной интерес представляет ИОЭ.

Пусть исходное расположение статистической характеристики объекта задано кривой 1 на рис. 2.10, которая имеет максимальное значение при 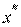. Пусть далее произошло смещение характеристики по оси 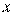и значение 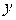упало с до .

При этом ясно, что измеряя только 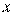и 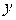нельзя определить направление смещения.

А вот если бы мы знали еще и скорость , то проблема была бы решена.

Рис.2.10 Рис.2.11

Из рисунка 2.11 следует, что закон экстремального управления должен удовлетворять условию

при поиске максимума.

Таким образом, чтобы принять решение о том, куда двигаться, нужно менять 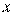и определять .

Отсюда следует правило: чтобы определить направление движения к экстремуму необходимо изменить входную величину и проанализировать реакцию на это изменение.

В отличие от обычных САР управление в ЭС носит дуальный характер, т.е. служит и для определения направления движения и для осуществления самого движения к экстремуму. Поэтому его часто делят на два вида – пробное и рабочее. Эти движения связаны между собой по- разному. Можно выделить три случая.

1) Пробное и рабочее движения разделены.

2) Пробное и рабочее движения совпадают.

3) Пробное и рабочее движение существуют одновременно.

Типы экстремальных систем

Замечание.

Градиентом называют векторную функцию скалярного аргумента. Компонентами вектора градиента являются частные производные аргумента по пространственным координатам. Градиент переменной 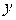записывается .

Обычно для определения проекций градиента используется следующий прием .

Шаговые ЭС.

Как уже отмечалось, для определения направления движения к экстремуму нужно знать . В шаговых ЭС бесконечно малые и заменяются малыми конечными приращениями и . Соответственно .

Алгоритм включает следующие шаги:

● даем приращение ,

● определяем ,

● по отношению этих приращений определяем рабочие точки относительно экстремума.

Существует 2 типа ШЭС:

а) с разделенными пробными и рабочими шагами, как это показано на рис. 2.15,

б) с совмещенными пробными и рабочими шагами.

Рис.2.15

Основной элемент ШЭС – устройство определяющее приращение входной или выходной величины.

Техническая реализация может быть весьма разнообразной. Чтобы повысить помехозащищенность и улучшить работу шаговой системы, часто используют дискретные системы шагового типа, в которых используют импульсные элементы, как это показано на рис. 2.16, 2.17.

Рис. 2.16 ШЭС с импульсными элементами.

Достоинства ШЭС.

● Очень удобно при регулировании медленно протекающих процессов. Вместо медленного изменения управляющего воздействия использована импульсная перестановка управляющего элемента.

● Хорошо работают с объектами с запаздыванием

Многомерные ЭС

Многомерные ЭС предполагают наличие объекта управления с экстремальной характеристикой, состояние которого зависит от нескольких входных переменных. На рис. 2.27 показана общая структура многомерных ЭС.

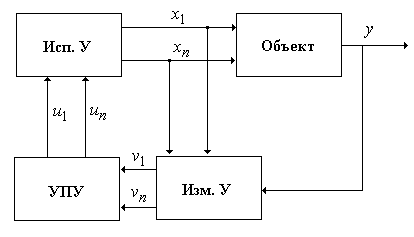
Рис. 2.27. Структура многомерной ЭС

Особенности данной системы связаны с блоками УПУ и Изм.У.

Пусть имеем зависимость 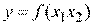. Изобразим 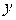на плоскости линиями уровня для значений …

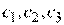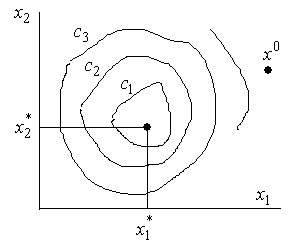
Рис. 2.28 Постановка задачи двумерного экстремального поиска

Пусть начальная точка состояния системы соответствует 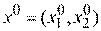. Алгоритм поиска может быть следующим.

: а) получить информацию о поведении функции в окрестности рабочей точки;

б) организовать движение системы (формулирование управляющих воздействий) в требуемом направлении.

Градиентные методы

Среди детерминированных способов наиболее эффективными в системах адаптивного управления являются градиентные методы. Градиентные методы основаны на использовании градиента целевой функции. Указанные методы носят итеративный характер, так как компоненты градиента являются, как правило, нелинейными функциями управляемых переменных.

Основная идея всех градиентных методов состоит в том, чтобы двигаться к минимуму в направлении наиболее быстрого убывания функции, которое определяется антиградиентом. Эта идея может реализоваться, например, следующим образом.

Выберем каким-либо способом начальную точку, вычислим в ней градиент рассматриваемой функции и сделаем небольшой шаг в обратном, антиградиентном направлении. В результате мы придем в точку, в которой значение функции будет меньше первоначального. В новой точке повторим процедуру: снова вычислим градиент функции и сделаем шаг в обратном направлении. Продолжая этот процесс, мы будем двигаться в сторону убывания функции.

Наглядной интерпретацией задачи градиентного спуска можно считать положение человека, который хочет максимально быстро спуститься на дно котловины, заросшей лесом, но видит перед собой лишь ограниченный участок местности. В такой ситуации логичным алгоритмом действия является движение в ту сторону, где местность наиболее круто идет вниз, т.е. в сторону антиградиента функции высоты.

Далее везде будем предполагать, что 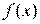, 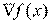существуют и непрерывны. Предполагается, что компоненты градиента могут быть записаны в аналитическом виде или с достаточно высокой точностью вычислены при помощи численных методов.

Замечание. В практических задачах найти значения производных целевых функций вида 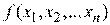аналитически, как правило, не удается и их вычисляют приближенно:

.

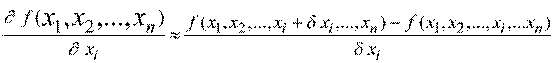Выбор величин приращений по координатам 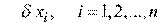зависит от возможностей используемой ЭВМ и необходимой точности вычислений.

Все градиентные методы поиска минимума основаны на итерационной процедуре, реализуемой в соответствии с формулой

,

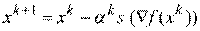где 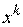– текущее приближение к решению ;

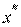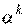– параметр, регулирующий длину 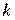-го шага;

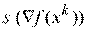– направление поиска в 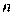- мерном пространстве управляемых переменных , .

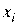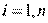Способ определения 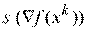и 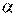на каждой итерации связан с особенностями применяемого метода.

Ранее уже отмечалось, что градиент функции 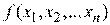в точке 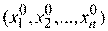− это вектор

,

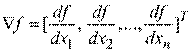проекции которого являются производными по координатам и вычислены для 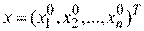. Длина вектора градиента

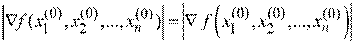(2.1)

характеризует скорость возрастания функции в этой точке, а направление соответствует направлению быстрейшего возрастания функции. Антиградиент - это вектор такой же длины, направленный в противоположную сторону (рис. 2.29). В точке минимума градиент функции равен нулю.

Единичный вектор градиента определяется как

.

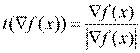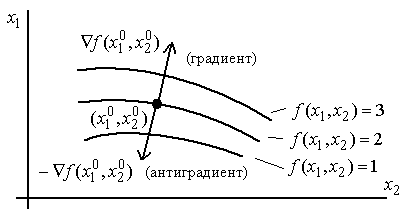
Рис. 2.29. Градиент и антиградиент функции

При поиске минимума каждая следующая точка поиска 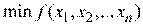(каждый новый член минимизирующей последовательности) получается в результате перемещения из предыдущей точки по направлению антиградиента целевой функции по формуле

.

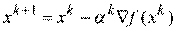Если в результате этого перемещения наблюдается увеличение значения целевой функции, то значение рабочего шага поиска уменьшается. Поиск прекращается, когда выполняется необходимое условие 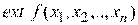, например, длина вектора градиента становится меньше требуемой точности:

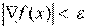. (2.2)

Различают методы градиента с переменным шагом и с постоянным шагом (рис. 2.30). При использовании метода градиента с переменным шагом изменение значений 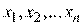производится согласно выражению

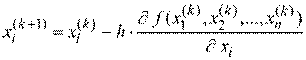, i=1,2,...,n , k=0,1,2…, (2.3)

а останов поиска - при выполнении неравенства (2.2). При возникновении ситуации 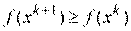значение параметра h уменьшается, например, делится на число 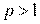. Характер изменения значений 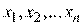, согласно (2.3), зависит от величины и знака соответствующих частных производных целевой функции.

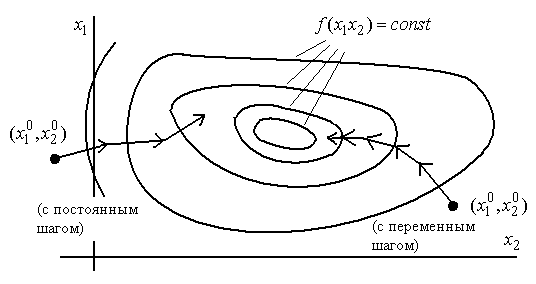
Рис. 2.30. Методы с постоянным и переменным шагом

К недостаткам метода можно отнести то, что, во-первых, на каждом шаге необходимо определять значение градиента. Это может быть не просто, если градиент определяется экспериментально. Во-вторых, по мере приближения к точке 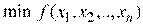абсолютные величины частных производных уменьшаются, следовательно, и шаг поиска является переменным – уменьшается по мере приближения к искомой точке. Такой характер поиска 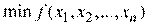требует иногда весьма значительных затрат времени.

Второй из отмеченных недостатков может быть устранен применением метода градиента с постоянным шагом. Метод позволяет сократить затраты времени, но требует несколько большего объема вычислений при изменении значений аргументов целевой функции. Его основное соотношение:

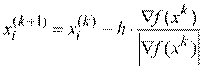, i=1,2,...,n; k=0,1,2,... . (2.4)

Метод использует вектор градиента единичной длины, который определяет лишь направление градиента, поэтому движение по 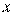осуществляется с постоянной скоростью, зависящей от величины шага 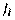. Если изменение аргументов целевой функции в соответствии с (2.4) приводит к увеличению ее значения, параметр поиска 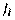уменьшается. Останов поиска 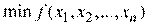по методу градиента с постоянным шагом осуществляется при выполнении неравенства .

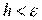Метод Коши (Наискорейшего спуска)

Вычисление градиента на каждом шаге, позволяющее все время двигаться в направлении наиболее быстрого убывания целевой функции, может в то же время замедлить вычислительный процесс. Дело в том, что подсчет градиента - обычно гораздо более сложная операция, чем подсчет самой функции, особенно если аналитическое выражение градиента отсутствует. Поэтому часто пользуются модификацией градиентного метода, получившей название метода наискорейшего спуска или метода Коши (рис.2.31).

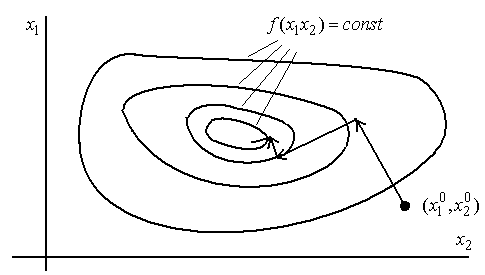
Рис. 2.31. Иллюстрация к методу наискорейшего спуска

Согласно этому методу после вычисления градиента функции в начальной точке делают в направлении антиградиента не маленький шаг, а движутся до тех пор, пока функция убывает. Достигнув точки минимума на выбранном направлении, снова вычисляют градиент функции и повторяют описанную процедуру. При этом градиент вычисляется гораздо реже, только при смене направлений движения.

Хотя траектория ведет к цели не так быстро, как на рис. 2.30, экономия машинного времени за счет более редкого вычисления градиента может быть весьма существенной.

Метод может быть реализован в нескольких вариантах. Простейшим является использование формулы

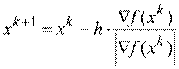
для последовательного движения к экстремуму, пока будет выполняться условие 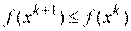. Нарушение данного условия означает прохождение точки минимума и говорит о том, что необходимо изменить направление движения. В достигнутой точке производится новый расчет вектора градиента и процесс повторяется.

Другой вариант состоит в том, что значение шага оптимизации 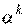вычисляется путем решения задачи минимизации 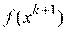вдоль направления 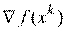с помощью того или иного метода одномерного поиска. Этот вариант реализации алгоритма более сложный, но обычно требует меньшего количества итераций.

Пусть функция 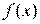дифференцируема по 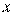и вектор градиента может быть записан аналитически. Тогда поиск минимума функции с использованием процедуры одномерной минимизации включает следующие этапы.

Этап 1. Определение аналитических соотношений для вычисления градиента функции 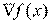, длины вектора градиента 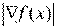и единичного вектора градиента .

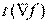Этап 2. Выбор исходной точк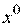и при 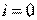(начальных значений аргументов функции).

Этап 3. Выбор шага a изменения координат текущей точки 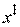. Осуществляется из условия достижения экстремума функции 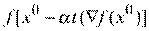одного аргумента 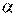в соответствии с уравнением

.

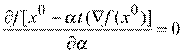Корень этого уравнения, соответствующий минимуму функции 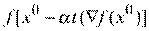, обозначим .

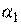Этап 4. Следующее приближение 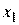вычисляется по формуле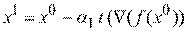

Этап 5. Производится возврат к этапу 3.

В результате формируется последовательность приближений 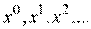. Вычислительный процесс заканчивается, когда будет достигнута точка 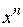, в которой оценка градиента будет равна нулю (коэффициенты функции отклика становятся незначимыми).

Пример. Выполнить шаг наискорейшего спуска для функции вида

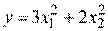
Решение.

Этап 1. Общий вид градиента функции :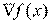

, ,

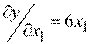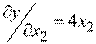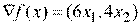
Длина вектора градиента:

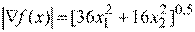
Этап 2. Выбор начальной точки, например .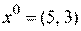

Этап 3. Вычисление координат единичного вектора градиента

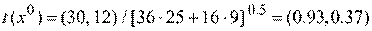
Координаты точки 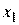при движении по направлению вектора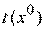

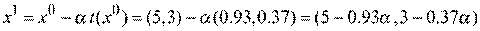
Запишем выражение для функции у в точке 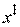как функцию от :

.

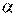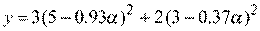Этап 4. Выбор шага а изменения координат текущей точки. Найдя производную от 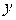по 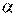в точке 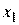и приравняв ее к нулю получим 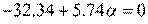. Следовательно, шаг .

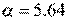Этап 5. Делаем шаг в направлении антиградиента. Координаты точки 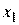после выполнения первого шага наискорейшего спуска по формуле

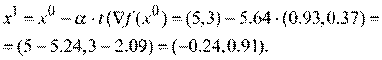
Аналогично выполняется следующий шаг наискорейшего спуска.

Рассмотренный алгоритм применяют только для нелинейныхфункций. Если функция отклика является линейной, то выбор оптимального значения параметра a невозможен. В этом случае шаг выбирается исходя из эвристических предположений исследователя о виде функции отклика.

Шаг 1.

При 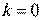вводятся исходные данные .

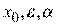Шаг 2.

Осуществляется циклический по 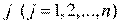покоординатный спуск из точки 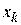по формуле:

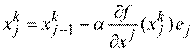
Шаг 3.

Если 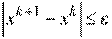, то поиск минимума заканчивается, причем:

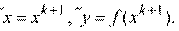
Иначе 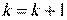и переходим к шагу 2.

Если же шаг á_к выбирается из условия минимума функции

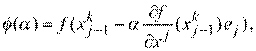
то мы получаем аналог метода наискорейшего спуска, называемый обычно методом Гаусса – Зейделя.

Шаг 1.

При 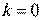вводятся исходные данные .

Шаг 2.

Осуществляется циклический по 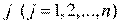покоординатный спуск из точки 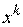по формулам:

где является решением задачи одномерной минимизации функции:

Шаг 3.

Если 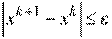, то поиск минимума заканчивается, причем:

Иначе 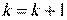и переходим к шагу 2.

Методы случайного поиска

При определенных условиях методы случайного поиска могут оказаться более эффективными, чем регулярные. Рассмотрим некоторые наиболее распространенные методы случайного поиска.

БАС с эталонной моделью

БАС с использованием анализатора характеристик требует наличия специальной процедуры (программной, аппаратной) определения характеристик, что усложняет систему и увеличивает время самонастройки. Вместе с тем, если есть возможность построить модель, описывающую желаемое поведение системы, уже по разности выходных сигналов модели и реальной системы можно судить о настройке регулятора и использовать эту разность для целенаправленной коррекции параметров.

К наиболее популярным в классе АС прямого действия относятся АС с эталонной моделью, функциональная схема которых представлена на рис. 4.5.

К достоинствам этого типа систем можно отнести:

● Формирование алгоритмов адаптации на основании измеряемых (а не вычисляемых) величин и относительная простота реализации;

● Возможность исключения пробных движений.

ЭМ может использоваться для решения следующих задач:

● Формирование эталонной траектории, реализующей желаемые динамические и статические характеристики;

● Формирование желаемой параметрической модели основного контура;

● Обучение регулятора адаптаций с помощью изменяемой ЭМ, что позволяет унифицировать алгоритмы адаптивного управления для изменяющихся ситуаций;

● Адаптивное управление по неполным данным на основе использования наблюдателей состояния;

● Восстановление работоспособности системы.

Адаптивные системы управления с эталонной моделью содержат динамическую модель системы, обладающую требуемым качеством и называемую эталонной моделью. Адаптивная система управления с эталонной моделью (ЭМ), кроме основного контура, содержащего регулятор (Р) и объект (О), включает контур с ЭМ и вычислительно-исполнительное устройство (ВИУ). Эталонная модель вырабатывает желаемый (эталонный) выходной сигнал. Эталонная модель и основной контур соединены параллельно.

Рис. 4.5. БАС с эталонной моделью

Вычислительно-исполнительное устройство (его также называют механизмом адаптации) обрабатывает разностный сигнал (разность между фактическим и эталонным сигналами) и подает его на алгоритм адаптации АА, который производит подстройку параметров регулятора. Выбор эталонной модели является частью процесса синтеза адаптивной системы управления.

Эталонная модель должна удовлетворять двум требованиям:

● с одной стороны, она должна отражать все требования к качеству синтезируемой системы,

● с другой стороны, эталонная реакция должна быть достижима для основного контура.

Последнее требование накладывает ограничения на структуру эталонной модели, определяемой предполагаемой структурой основного контура.

Регулятор должен обладать идеальной следящей способностью. Другими словами, закон (алгоритм) управления должен быть таким, чтобы существовали такие значения его параметров, называемые идеальными, при которых передаточная функция основного контура относительно задающего воздействия и выхода равна передаточной функции эталонной модели. Принцип работы адаптивной системы с ЭМ состоит в том, чтобы адаптор обеспечивал сходимость к нулю ошибки слежения — разность между выходными сигналами основного контура