Применение определителей к исследованию и решению системы линейных уравнений.
Рассмотрим систему n линейных уравнений с n неизвестными:
а11х1 + а12х2 + . . . + а1пхп = b1 ,
а21х1 + а22х2 + . . . + а2пхп = b2 ,
. . . . . . . . . . . .
ап1 х1 + ап2х2 + . . . аппхп = bп.
1) Если определитель системы
Δ = 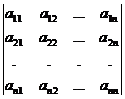 ≠ 0,
≠ 0,
то система имеет единственное решение, определяемое формулами Крамера:
хi = 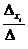 ,
,
где Δ хi – определитель, полученный из Δ заменой элементов i столбца на столбец свободных членов.
2) Если Δ = 0, а среди определителей Δ хi есть не равные нулю, то система не имеет решения.
3) Если Δ = Δ х1=Δ х2=. . .=Δ хk = 0 , причем один из миноров (п – 1) –го порядка определителя Δ не равен нулю. Тогда система сводится к п – 1 уравнениям; в этом случае одно из уравнений есть следствие остальных. Одному из неизвестных можно дать произвольное значение. Остальные неизвестные определяются единственным образом из системы п – 1 уравнений.
Пример 1: Решить систему уравнений:
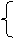 2х – 3у = 7,
2х – 3у = 7,
- х + 5у = -7.
Решение:
Здесь Δ = 7; Δх = 14; Δу = - 7.
Δ ≠ 0, следовательно система имеет единственное решение, определяемое формулами Крамера:
хi = 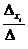 .
.
Тогда х = 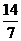 = 2, у =
= 2, у = 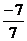 = -1.
= -1.
Ответ: х = 2, у = -1.
Пример 2: Решить систему уравнений:
- 3х + у + 2z = -2,
- х - 2у - 3z = -5,
х + у + 3z = 0.
Решение:
Здесь Δ = 11, Δх = 11,Δу = 55 ,Δz = -22.
Δ ≠ 0, следовательно система имеет единственное решение, определяемое формулами Крамера:
хi = 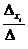 .
.
Тогда х = 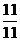 = 1, у =
= 1, у = 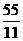 = 5, z =
= 5, z = 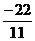 = -2.
= -2.
Ответ: х = 1, у = 5, z = -2.
Пример 3: Решить систему уравнений:
х1 - х2 + 2х3 - х4 = 1,
х1 + х2 + х3 + х4 = 4,
2х1 + 3х2 - 5х4 = 0,
5х1+2х2 + 5х3 - 6х4 = 0.
Решение:
Здесь Δ = Δ х1=Δ х2=. . .=Δ хk = 0.
Вычеркнув четвертую строку и четвертый столбец, получим минор
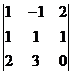 = -3 ≠ 0
= -3 ≠ 0
Система сводится к трем уравнениям:
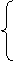 х1 - х2 + 2х3 – х4 = 1,
х1 - х2 + 2х3 – х4 = 1,
х1 + х2 + х3 + х4 = 4,
2х1 + 3х2 – 5х4 = 0.
Четвертое уравнение есть их следствие. Неизвестному х4 можно дать любое значение. Из последней системы находим:
х1 = 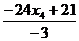 , х2 =
, х2 = 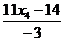 , х3 =
, х3 = 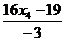 .
.
Ответ: {( х1, х2, х3, х4)| х4 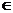 R, х1 =
R, х1 = 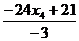 , х2 =
, х2 = 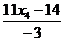 , х3 =
, х3 = 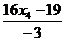 }.
}.
٭ ٭
٭
14. Решить систему уравнений методом последовательного исключения неизвестных:
| a) -3х1 + 2х2 – 4х3 + х4 = -8, -5х1 – 3х3 + 2х4 = -6, х1 – 3х2 – х3 + 4х4 = 7, 2х1 + 5х2 + 3х4 = 0; | b) 5х1 - 3х2 + 7х3 + х4 = 5, х1 + х2 – 5х3 + 3х4 = -7, 3х1 - х2 + х3 + 2х4 = 1, 2х1 – 3х3 + х4 = 2. |
15. Решить систему уравнений методом последовательного исключения неизвестных:
| а) х1– 5х2 + х3 – 3х4 = -4, -4х1 + 2х2 + 3х3 + х4 = 5, 2х1 + х2 – 4х4 = 8, -х1 + 6х2 – 2х3 + х4 = 6; | b) 2х1– х2 + х3 – 2х4 = -3, 3х1 + 2х2 – х3 – 4х4 = -7, х1 – 3х2 + 2х4 = -2, -2х1 + 3х3 – х4 = 7. |
16. Решить систему уравнений методом последовательного исключения неизвестных:
| а) -2х1– х2 + 3х3 – х4 = 0, 3х1 – 4х3 + 2х4 = 4, х1 + 3х2+2х3 – х4 = 5, -4х1 – 5х2 + х3 +3х4 = -2; | b) 2х1– х2 – 3х3 + х4 = 0, -х1 + 5х2 + х3 + 2х4 = 12, х1 + х2 – 2х3 + 3х4 = 3, 3х1 + х3 – 5х4 = 0. |
17. Решить систему уравнений методом последовательного исключения неизвестных:
| а) х1– 2х2 + 3х3 – 4х4 = 6, 2х1 + х2 – 4х3 – 3х4 = 2, 3х1 + 4х2 – х3 + 2х4 = 8, -4х1 – 3х2 + 2х3 +х4 = 2; | b) х1+ 5х2 – 2х3 + 3х4 = -1, -х1 + 4х2 + 3х3 + 2х4 = -8, х1 – 7х3 – 3х4 = 2, 3х1 – 2х2 + х3 – х4 = 4. |
18. Решить систему уравнений методом последовательного исключения неизвестных:
| а) х1+ 3х2 – 5х3 – 2х4 = -10, 2х1 – х2 + 3х3 + х4 = -2, х1 + 2х2 – 2х3 – х4 = -6, х2 – 2х3 + 3х4 = 1; | b) 2х1– 3х2 + х3 – 4х4 = 9, -х1 – 2х2 + 3х3 + х4 = 8, 3х1 – х2 + 2х3 – 2х4 = 11, х1 + 4х2 – х3 + 3х4 = -6. |
19. Решить систему уравнений методом последовательного исключения неизвестных:
| а) 3х1– х2 + 2х3 + х4 = 1, 2х1 + 3х2 + 4х3 – 2х4 = 3, х1 + 5х2 + 3х3 – х4 = 4, - х1 – 2х3 + 3х4 = 2; | b) -2х1+ 4х2 – 3х3 + 5х4 = -5, 3х1 – 2х2 + х3 – 4х4 = 8, 4х1 + х2 – 2х3 + 3х4 = 6, -5х1 – 3х2 – х4 = 6. |
20. Решить систему уравнений:
а) 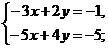 b)
b) 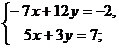
21. Решить систему уравнений:
а) 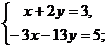 b)
b) 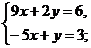
22. Решить систему уравнений:
а) 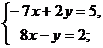 b)
b) 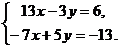
23. Решить систему уравнений:
а) 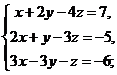 b)
b) 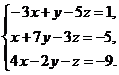
24. Решить систему уравнений:
а) 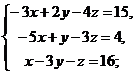 b)
b) 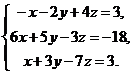
25. Решить систему уравнений:
а) 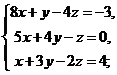 b)
b) 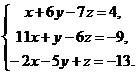
26. Решить систему уравнений:
| а) х1– х2 + 3х3 – х4 = 6, 3х1 – 2х3 + 2х4 = 4, х1 + 3х2+2х3 – х4 = 1, - х1 – 5х2 + х3 +3х4 = 4; | b) 2х1– х2 – 3х3 + х4 = -13, -х1 + 5х2 + х3 – 8х4 = 5, х1 + 4х2 – 2х3 + 5х4 = -8, 3х1 + х3 – 5х4 = -3. |
27. Решить систему уравнений:
| а) 5х1+ х2 – 2х3 – 9х4 = 9, 3х1 – х3 + 7х4 = 5, -2х1 + 3х2 + х3 + 2х4 = -4, -4х1 + х2 – 2х3 + 5х4 = 0; | b) х1– 2х2 – х3 + 5х4 = 12, -2х1 + 3х2 + 6х3 + х4 = -6, х1 – 7х2 + 2х3 + х4 = 1, 3х1 + х2 – 2х4 = -1. |
Глава 2. Элементы аналитической геометрии
§1.Простейшие задачи аналитической геометрии
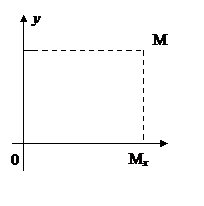
1.1. Декартовы прямоугольные координаты на плоскости. Пусть на плоскости задана декартова прямоугольная система координат xOy. Координатами произвольной точки М в заданной системе называют числа
х = ОМх, у = ОМу

|
|
Пример. Найдите координаты точек, симметричных точке М относительно осей и начала координат, если М (3; -2).
Решение.
Точка М (3;-2) лежит в четвертой четверти. Точка М1, симметричная точке М относительно оси абсцисс будет располагаться в первой четверти. При этом она будет иметь туже абсциссу, что и точка М, а знак ординаты изменится на противоположный. Следовательно координаты точки М1(3;2).
Точка М2, симметричная точке М относительно оси ординат будет располагаться в третьей четверти. Она будет иметь туже ординату, что и точка М, а знак абсциссы изменится на противоположный. Следовательно координаты точки М2(-3;-2).
Точка М3, симметричная точке М относительно начала координат будет располагаться во второй четверти. При этом знаки абсциссы и ординаты изменятся на противоположные. Следовательно, координаты точки М3(-3;2).
Ответ: М1(3; 2); М2(-3; -2); М3(-3; 2).
1.2. Полярные координаты точки. Связь полярных и декартовых координат точки. Пусть на плоскости задана полярная система координат, которая определяется некоторой точкой О, называемой полюсом, исходящим из этой точки лучом ОА, называемым полярной осью и единичным отрезком ОЕ, принадлежащим полярной оси. Полярными координатами произвольной точки М называют числа ρ = ОМ и Ө = Ð АОМ (рис. 2.).

Если полюс полярной системы координат совпадает с началом декартовых прямоугольных координат, а полярная ось совпадает с положительной полуосью абсцисс, то переход от полярных координат произвольной точки к декартовым координатам той же точки осуществляется по формулам
х = ρ cos Ө, y = ρ sin Ө.
В этом же случае формулы
ρ = 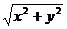 , tg Ө =
, tg Ө = 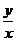
являются формулами перехода от декартовых координат к полярным.
Пример 1. В полярной системе координат даны точки A(1;- 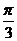 ), B(2;
), B(2; 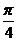 ). Найти их декартовы координаты.
). Найти их декартовы координаты.
Решение.
Переход от полярных координат произвольной точки к декартовым координатам той же точки осуществляется по формулам
х = ρ cos Ө, y = ρ sin Ө.
Найдем декартовы координаты точки А.
х = 1 cos (- 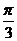 ) =
) =  , y = 1 sin (-
, y = 1 sin (- 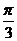 ) = -
) = - 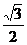 .
.
Следовательно точка А (  ;-
;- 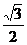 ).
).
Найдем декартовы координаты точки В.
х = 2 cos 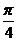 =
= 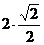 =
= 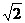 , y = 2 sin
, y = 2 sin 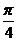 =
= 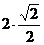 =
= 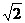 . Точка В (
. Точка В ( 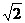 ;
; 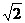 ).
).
Ответ: А (  ;-
;- 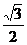 ), В (
), В ( 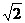 ;
; 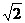 ).
).
Пример 2. В полярной системе координат даны точки А(1;- 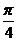 ) и В(4;
) и В(4; 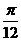 ). Найти длину отрезка АВ и площадь треугольника ОАВ.
). Найти длину отрезка АВ и площадь треугольника ОАВ.
Решение.
Рассмотрим треугольник АОВ (рис. 3.).
Угол Ð АОВ = Ө2 - Ө1. Следовательно Ð АОВ = 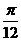 - (-
- (- 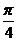 ) =
) = 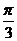 .
.
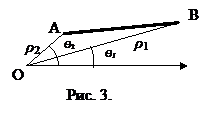 Найдем длину отрезка АВ по теореме косинусов:
Найдем длину отрезка АВ по теореме косинусов:
с 2 = в2 + а 2 – 2ав cos γ.
В нашем случае
а = ρ1 = 1, в = ρ2 = 4, Ð γ = Ð АОВ = 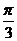 .
.
Тогда АВ2 = 42 + 12 + 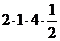 = 16 + 1 + 4 = 21. АВ =
= 16 + 1 + 4 = 21. АВ = 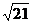 (ед.)
(ед.)
Площадь треугольника ОАВ найлем по формуле:
S∆ =  ρ1 ρ2sinα.
ρ1 ρ2sinα.
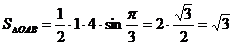 (кв.ед)
(кв.ед)
Ответ: АВ = 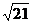 ед.,
ед., 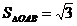 кв.ед.
кв.ед.
1.3. Длина и полярный угол отрезка. Расстояние между двумя точками.Если известны координаты точек А (х1; у1) и В (х2; у2), то проекции Х и Y на оси координат отрезка АВ вычисляются по формулам
Х = х2 - х1, Y = у2 - у1.
Угол Ө между прямой АВ и положительным направлением оси абсцисс называется полярным углом отрезка АВ.
Формулы
Х = d cos Ө, Y= d sin Ө
выражают проекции произвольного отрезка на координатные оси через его длину и полярный угол. Из них вытекают формулы
d = 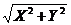 , cos Ө =
, cos Ө = 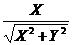 , sin Ө =
, sin Ө = 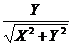 ,
,
выражающие длину и полярный угол отрезка через его проекции на оси координат.
Если на плоскости даны две точки А (х1; у1) и В (х2; у2), то расстояние d между ними определяется формулой
d = 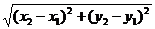 .
.
Пример 1. Даны точки А(-6;1) и В(-3;-3). Найти длину и полярный угол отрезка АВ.
Решение.
Длина и полярный угол отрезка через его проекции на оси координат выражаются следующим образом :
d = 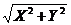 , cos Ө =
, cos Ө = 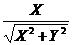 , sin Ө =
, sin Ө = 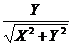 ,
,
где Х и Y проекции отрезка АВ на оси координат: Х = х2 - х1, Y = у2 - у1.
Х = -3 – (-6) = 3; Y = -3 – 1 = - 4,
d = 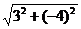 =
= 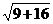 =
= 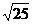 = 5,
= 5,
cos Ө = 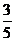 ; Ө = arcos
; Ө = arcos 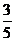 , Ө = 530.
, Ө = 530.
Ответ: d = 5, Ө = 530.
Пример 2. Найти площадь равностороннего треугольника, если две его вершины имеют координаты (0; 7), (4; -5).
Решение.
Найдем площадь равностороннего треугольника по формуле S = 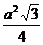 .
.
Зная, что расстояние между двумя точками определяется по формуле
d = 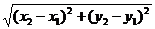 , вычислим длину стороны треугольника.
, вычислим длину стороны треугольника.
а = 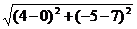 =
= 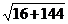 =
= 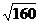 = 4
= 4 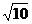 .
.
Тогда S = 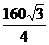 = 40
= 40 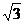 (кв. ед.).
(кв. ед.).
Ответ: SΔ = 69,3 кв.ед.
1.4. Деление отрезка в данном отношении.Если точка М (х;у) лежит на прямой, проходящей через две данные точки А (х1; у1) и В (х2; у2) и дано отношение λ = 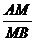 , в котором точка М делит отрезок АВ, то координаты точки М определяются по формулам
, в котором точка М делит отрезок АВ, то координаты точки М определяются по формулам
х = 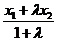 , у =
, у = 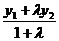 .
.
Если точка М является серединой отрезка АВ, то ее координаты вычисляются по формулам
х = 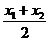 , у =
, у = 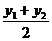 .
.
Пример. Найти координаты точки М, которая делит отрезок АВ в отношении λ = 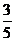 , если А (-1;5), В (7;2).
, если А (-1;5), В (7;2).
Решение.
Найдем координаты точки М зная, что они определяются по формулам
х = 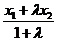 , у =
, у = 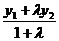 .
.
х = 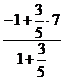 =
= 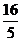 :
: 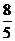 =
= 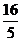
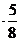 = 2; у =
= 2; у = 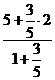 =
= 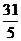 :
: 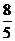 =
= 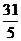
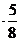 =
= 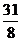 = 3
= 3 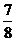 .
.
Ответ: М (2; 3 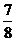 ).
).
1.5. Площадь треугольника.Пусть на плоскостиxOy заданы три точки А (х1; у1), В (х2; у2) и С (х3; у3). Тогда площадь S треугольника АВС вычисляется по формуле
SΔ = ±  | х2 – х1у2 – у1х3 – х1у3 – у1 | (*) |
Знак«+» берут в случае, если определитель больше нуля, знак « – », если определитель меньше нуля.
Пример: Найти площадь треугольника АВС, зная координаты его вершин: А (-3;1), В (7;-2), С (4;0).
Решение.
Зная, что площадь треугольника вычисляется по формуле (*).
Найдем SΔАВС = ±  ∙(10∙(-1) – (-3)∙7) = ±
∙(10∙(-1) – (-3)∙7) = ±  ∙ (-10 +21) =
∙ (-10 +21) =  ∙11 = 5,5 (кв.ед.).
∙11 = 5,5 (кв.ед.).
Ответ: SΔАВС = 5,5 кв.ед.
٭ ٭
٭
28. На координатной прямой, определить геометрическое место точек, координаты которых удовлетворяют неравенствам:
| а) | х | > 5; | e) | х + 1 | ≥ 4; | i) | х – 5 | ≤ 9; |
| b) | х | < 2; | f) | х + 6 | > 3; | j) | х – 2 | ≥ 7; |
| с) | х | ≤ 3; | g) | х + 3 | < 12; | k) | х – 1 | > 5; |
| d) | х | ≥ 7; | h) | х + 2 | ≤ 8; | l) | х – 4 | < 3. |
29. В декартовой прямоугольной системе координат построить точки А(0;3), В(-2;4), С(-5;0), D(4,1), Е(1 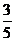 ;-0,8), F(-3,-2).
;-0,8), F(-3,-2).
30. Даны точки А(-1;2), В(3;8),C(0;5), D(-2;-4), E(-3;0). Найти координаты точек симметричных данным относительно: а) оси абсцисс; в) оси ординат; с) начала координат.
31. В полярной системе координат построить точки A(2; 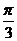 ), B(1;-
), B(1;- 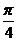 ), C(3;
), C(3; 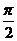 ), D(5;0), E(1,5;3
), D(5;0), E(1,5;3 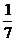 ), F(4,-1).
), F(4,-1).
32. В полярной системе координат даны точки A(1;- 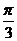 ), B(2;
), B(2; 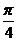 ), C(3;0), D(4;
), C(3;0), D(4; 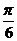 ), E(5;-
), E(5;- 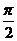 ), F(3;
), F(3; 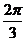 ). Найти координаты точек симметричных данным относительно: а) полярной оси; в) полюса.
). Найти координаты точек симметричных данным относительно: а) полярной оси; в) полюса.
33. В полярной системе координат дан параллелограмм ABCD, точка пересечения диагоналей которого совпадает с полюсом. Найти координаты вершин C и D, если координаты точек: А(2; 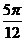 ), В(3;-
), В(3;- 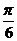 ).
).
34. В полярной системе координат дан отрезок АВ. Найти координаты его середины, если координаты точек: А(4;0), В(3; 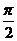 ).
).
35. В полярной системе координат дан отрезок АВ. Точка М(3; 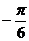 ) – середина отрезка АВ. Найти координаты точки В, если А(6;
) – середина отрезка АВ. Найти координаты точки В, если А(6; 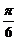 ).
).
Указание: показать, что треугольник АМО – прямоугольный.
36. В полярной системе координат даны точки А(2;- 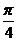 ) и В(5;
) и В(5; 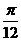 ). Найти длину отрезка АВ.
). Найти длину отрезка АВ.
37. Найти длину отрезка АВ, если точки А(3; 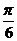 ), В(1;
), В(1; 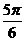 ) заданы в полярных координатах.
) заданы в полярных координатах.
38. В полярной системе координат даны две смежные вершины квадрата: А(3; 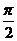 ) и В(2;-
) и В(2;- 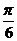 ). Найти его площадь.
). Найти его площадь.
39. В полярной системе координат даны две противоположные вершины квадрата: А(7;- 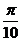 ) и С(3;
) и С(3; 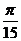 ). Найти его площадь.
). Найти его площадь.
40. Найти площадь треугольника ОАВ, если А(7; 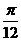 ), В(4;-
), В(4;- 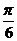 ), а третья вершина совпадает с полюсом.
), а третья вершина совпадает с полюсом.
41. Найти площадь треугольника ОАВ, если одна из его вершин находится в полюсе, координаты точек А(5; 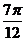 ) и В(4;
) и В(4; 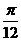 ).
).
42. В полярной системе координат даны две вершины правильного треугольника АВС. Найти его площадь, если координаты точек А(2; 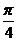 ), В(5;
), В(5; 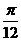 ).
).
43. Найти площадь треугольника, вершины которого А(5; 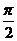 ), В(6;
), В(6; 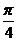 ), С(7;-
), С(7;- 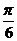 ) заданы в полярных координатах.
) заданы в полярных координатах.
44. Полюс полярной системы координат совпадает с началом декартовых прямоугольных координат, а полярная ось совпадает с положительной полуосью абсцисс. Найти полярные координаты точек А, В, С, D, E, F, если их декартовы координаты: А(7;0), В(3;3), С(-3;5), D(-3 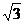 ;-3), E(-2;0), F(1;-
;-3), E(-2;0), F(1;- 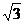 ).
).
45. Полюс полярной системы координат совпадает с началом декартовых прямоугольных координат, а полярная ось совпадает с положительной полуосью абсцисс. Найти декартовы координаты точек А, В, С, D, E, F, если их полярные координаты: А(3;- 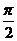 ), В(2
), В(2 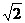 ;-
;- 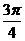 ), С(5;
), С(5; 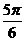 ), D(4;
), D(4; 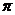 ), E(7;
), E(7; 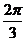 ), F(1;
), F(1; 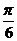 ).
).
46. Полюс полярной системы координат совпадает с началом декартовых прямоугольных координат, а полярная ось совпадает с положительной полуосью абсцисс. Декартовы координаты точек A(-2; 2), B(-7; 0), C(3;-5), D(10; 6), E(0; -2), F(-5;-3). Определить их полярные координаты.
47. Полюс полярной системы координат совпадает с началом декартовых прямоугольных координат, а полярная ось совпадает с положительной полуосью абсцисс. Полярные координаты точек A(2; - 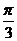 ), B(3;-
), B(3;- 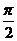 ), C(5;-
), C(5;- 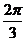 ), D(1;-
), D(1;- 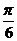 ), E(3;
), E(3; 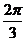 ), F(
), F( 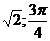 ). Определить их декартовы координаты.
). Определить их декартовы координаты.
48. Установить, какие линии задаются в полярных координатах уравнениями: а) ρ = 3; b) ρ sin φ = 0; с) cos φ =  ; d) ρ = 8 cos φ. Построить их в декартовой системе координат.
; d) ρ = 8 cos φ. Построить их в декартовой системе координат.
49. Установить, какие линии задаются в полярных координатах уравнениями: а) ρ = 4; b) ρ cos φ = 5; с) sin φ = 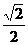 ; d) ρ = 8 sin φ. Построить их в декартовой системе координат.
; d) ρ = 8 sin φ. Построить их в декартовой системе координат.
50. Даны точки: А(-2;3), В(-1;4), С(1;7), D(4;8). Найти длину и полярный угол отрезков: а) АВ; в) АС; с) ВD; d) DC.
51. Даны точки А(-1;9), В(2;5), С(-3;5). Найти периметр и площадь треугольника АВС.
52. Даны две смежные вершины квадрата: А(2;-5), В(-3;1). Найти его площадь.
53. Даны две противоположные вершины квадрата: А(-3;8), С(4;-7). Найти его площадь.
54. Найти площадь правильного треугольника, две вершины которого имеют координаты: А(-2;-5), В(8;-7).
55. Сторона ромба равна 5, две его противоположные вершины имеют координаты: А(1;0), С(-3;2 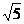 ). Найти его площадь.
). Найти его площадь.
56. Дана точка А(3;2). Найти на координатных осях точки расстояние до которых от точки А равняется 5.
57. Даны вершины треугольника: А(-3;7), В(2;5), С(4;-3). Найти координаты середин его сторон.
58. Даны три точки: А(-2;7), В(2;1) и С(4;-2). Определить отношение λ, в котором каждая из них делит отрезок, ограниченный двумя другими.
59. Даны точки А(-3;-2) и В(6;7). Найти координаты точки, которая делит отрезок АВ в отношении: а) λ =  ; b) λ =
; b) λ = 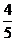 ; с) λ = -4.
; с) λ = -4.
60. Даны точки А(-7;6) и В(5;-2). Найти координаты точки, которая делит отрезок АВ в отношении: а) λ = 3; b) λ = 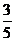 ; с) λ = -5.
; с) λ = -5.
61. Определить координаты концов отрезка АВ, который точками N(-3;-5) и M(2;1) разделен на три равные части.
62. Доказать, что точки: А(-2;-4), В(-6;4), С(4;-1) – вершины прямоугольного треугольника.
63. Доказать, что точки: А(-9;-1), В(-3;1), С(5;3 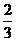 ) лежат на одной прямой.
) лежат на одной прямой.
64. Найти площадь треугольника, координаты вершин которого:
а) А(1;5), В(-2;3), С(-7;-2);
b) А(2;3), В(-6;1), С(-3;-4);
с) А(3;-5), В(-4;7), С(-2;5).
65. Вершины параллелограмма АВСD имеют координаты: А(2;-7), В(5;3), С(-1;6). Найти его площадь.
66. Площадь треугольника АВС равна 4 кв. ед. Две его вершины имеют координаты: А(1;2), В(-2;3), а третья вершина лежит на оси Оу. Найти координаты вершины С.
67. Площадь треугольника АВС равна 5 кв. ед. Две его вершины имеют координаты: А(1;2), В(-2;3), а третья вершина лежит на оси Ох. Найти координаты вершины С.
Линии первого порядка
2.1. Различные виды уравнения прямой. В декартовых координатах каждая прямая определяется уравнением первой степени и, обратно, каждое уравнение первой степени определяет прямую.
Уравнение вида Ах + Ву + С = 0, где А, В и С некоторые числа, а х и у – переменные, называется общим уравнением прямой.
Уравнение вида у = kх + b, где k и b некоторые числа, а х независимая переменная называется уравнением прямой, разрешенным относительно ординаты или уравнением прямой с угловым коэффициентом.
Уравнение вида 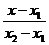 =
= 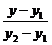 является уравнением прямой, проходящей через две точки М1(х1; у1) и М2(х2; у2).
является уравнением прямой, проходящей через две точки М1(х1; у1) и М2(х2; у2).
Уравнение вида  +
+ 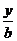 = 1, где a и b есть величины отрезков, отсекаемых прямой на координатных осях называется уравнением прямой «в отрезках».
= 1, где a и b есть величины отрезков, отсекаемых прямой на координатных осях называется уравнением прямой «в отрезках».
Пример. Прямая проходит через точки А(-4; 1) и В(-2; 2). Составить общее уравнение данной прямой и уравнение прямой в отрезках.
Решение.
Воспользуемся уравнением прямой, проходящей через две точки
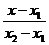 =
= 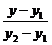 ,
,
Подставив координаты данных точек получаем:
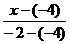 =
= 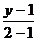 ;
;
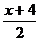 =
= 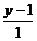 ;
;
-8(х +4) = 7 (у – 1);
х – 2у + 6 = 0 – общее уравнение данной прямой;
- 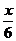 +
+ 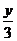 = 1 – уравнение данной прямой в отрезках.
= 1 – уравнение данной прямой в отрезках.
Ответ: х – 2у + 6 = 0; - 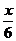 +
+ 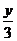 = 1.
= 1.
2.2. Угол между двумя прямыми. Условие параллельности и перпендикулярности двух прямых. Пусть две прямые заданы уравнениями
у = k1х +b1и у = k2х +b2,
тогда угол φ между этими прямыми определяется по формуле
tg φ = 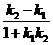 .
.
Признаком параллельности двух прямых является равенство их угловых коэффициентов k1= k2.
Если же прямые перпендикулярны, то их угловые коэффициенты обратны по абсолютной величине и противоположны по знаку, т.е. k2 = - 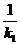 .
.
В случае, когда прямые заданы общими уравнениями
А1х + В1у + С1 = 0 и А2х + В2у + С2 = 0,
угол между ними определяется по формуле tg φ = 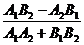 .
.
В этом случае признаком параллельности двух прямых является равенство 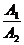 =
= 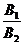 , а признаком их перпендикулярности равенство
, а признаком их перпендикулярности равенство 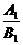 = -
= - 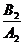 .
.
Пример: Найти угол φ между прямыми: 1) 2х – у + 6 = 0 и х + 3у -11 = 0; 2) у = -5х +7 и у = 2х - 8.
Решение.
1) Если прямые заданы общими уравнениями, то тангенс угла между ними вычисляется по формуле: tg φ = 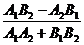 .
.
В нашем случае tg φ = 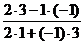 =
= 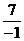 = -7, следовательно φ = -820.
= -7, следовательно φ = -820.
2) Если прямые заданы уравнениями с угловым коэффициентом, тангенс угла между ними вычисляется по формуле: tg φ = 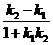 .
.
Тогда tg φ = 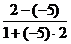 =
= 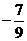 . Следовательно φ = - 380.
. Следовательно φ = - 380.
Ответ: 1) φ = -820; 2) φ = - 380.
2.3. Уравнение прямой, проходящей через данную точку параллельно данной прямой. Уравнение прямой, проходящей через данную точку перпендикулярно данной прямой.Прямая, проходящая через точку М(х1; у1) и параллельная прямой у = kх +b, задается уравнением
у – у1 = k (х – х1).
Прямая, проходящая через данную точку и перпендикулярная данной прямой, задается уравнением у – у1 = - 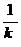 (х – х1).
(х – х1).
Если прямая задана общим уравнением Ах + Ву + С = 0, прямая проходящая через точку М(х1; у1) и параллельная данной прямой, задается уравнением А(х – х1) + В(у – у1) = 0, а перпендикулярная ей уравнением
А(у – у1) - В(х – х1) = 0.
Пример. Даны вершины треугольника АВС: А(-1;3), В(2;-5), С(7;0). Составить уравнение прямой параллельной ВС, проходящей через точку А и уравнение высоты, опущенной из вершины А.
Решение.
1) Составим уравнение прямой ВС: 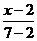 =
= 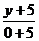 ;
; 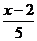 =
= 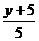 . Следовательно, прямая ВС задается уравнением: х – у – 7 = 0.
. Следовательно, прямая ВС задается уравнением: х – у – 7 = 0.
2) Составим уравнение прямой параллельной ВС, проходящей через точку А.
Уравнение прямой параллельной данной прямой Ах + Ву + С = 0 и проходящей через точку М(х1; у1), имеет вид А(х – х1) + В(у – у1) = 0.
Подставив значения, получаем: 1 ·(х – (-1)) + (-1) ·(у – 3) = 0.
Уравнение прямой имеет вид: х – у + 4 = 0.
3) Составим уравнение высоты, опущенной из вершины А.
Уравнение прямой перпендикулярной данной прямой Ах + Ву + С = 0 и проходящей через точку М(х1; у1), имеет вид А(у – у1)
