Напряженное состояние в точке деформируемого тела

Напряженное состояние в точке деформируемого тела характеризуется совокупностью напряжений на всех возможных площадках, проходящих через данную точку.

Достаточно знать напряжения на трех взаимно-перпендикулярных площадках, чтобы вычислить напряжения на любой площадке, проходящей через рассматриваемую точку. Совокупность напряжений на трех координатных площадках называется тензором напряжений.

T_s=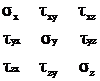

Площадки, на которых касательные напряжения равны нулю, называются главными площадками, а нормальные напряжения на этих площадках называются главными напряжениями, нумеруются в порядке убывания s_{1 ³} s_{2 ³} s₃ и находятся из кубического уравнения:

s³ - J₁×s² + J₂×s - J₃ = 0, (10)

где J₁ = s_x + s_y + s_z,

J₂ = s_xs_y + s_xs_z + s_zs_y - t_xy² - t_xz² - t_zy²,

J₃ = s_xs_ys_z - s_xt_zy² - s_yt_zx² - s_zt_xy² + 2t_xyt_zyt_xz.

Положение главных площадок задается направляющими косинусами

l_i = cos(x,n_i), m_i = cos(y,n_i), n_i = cos(z,n_i) нормалей n_i главных площадок

(i = 1, 2, 3). Для нахождения их величин используют два уравнения из системы

(s_x-s_i)×l_i + t_xy×m_i + t_xz×n_i = 0,

t_yx×l_i + (s_y-s_i)×m_i + t_yz×n_i = 0,

t_zx×l_i + t_zy×m_i + (s_z-s_i)×n_i = 0,

к которым следует присоединить дополнительное условие

l_i² + m_i² + n_i² = 1.

Здесь s_i - одно из трех главных напряжений. Различают следующие виды напряженных состояний: одноосное, двухосное и трехосное в зависимости от числа корней характеристического уравнения.

Наибольшие касательные напряжения возникают на площадках, равно наклоненных к первой и третьей главным площадкам, и равны

t_max = .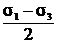

Рассмотрим теперь напряженное состояние в опасных точках стержня.

При поперечном изгибе в опасной точке поперечного сечения действуют нормальные напряжения от изгиба и касательные напряжения, вызванные поперечной силой.

При изгибе с кручением возникают нормальные напряжения от изгиба и касательные напряжения от кручения. В силу принятых гипотез в продольных сечениях стержня нормальные напряжения s_у и s_х равны нулю.

y

t_zx

t_xz

z s_z

Рис.10

Если в окрестностях опасной точки радиальным, тангенциальным и поперечным сечениями выделить бесконечно малый элемент, то на гранях его будут возникать только напряжения, показанные на рис.10. Заштрихованная грань элемента совпадает с поперечным сечением. Инварианты напряженного состояния будут

J₁ = s_z; J₂ = -t_zx²; J₃ = 0.

Следовательно, напряженное состояние будет двухосным и характеристическое уравнение примет вид

s(s²-J₁×s+J₂) = 0.

Один корень этого уравнения будет нулевой, т.е. одно главное напряжение равно нулю и два других определяются из квадратного уравнения и равны

s = .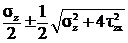

Таким образом, главные напряжения в стержне будут равны

s₁ = 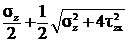, s₃ = .

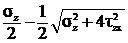Из рисунка 10 видно, что на площадке перпендикулярной оси Y отсутствуют касательные и нормальные напряжения, т.е. вторая главная площадка s₂ = 0 и направляющие косинусы нормали к этой площадке будут l₂ = 0, m₂ = 1, n₂ = 0.

Поскольку главные площадки взаимно перпендикулярны, то первая и третья главные площадки будут параллельны оси Y.

Следовательно,

m₁ = m₃ = 0 и нормали n₁ и n₂ будут параллельны плоскости XZ.

Для нахождения направляющих косинусов в этом случае можно воспользоваться каким-либо одним из уравнений. Найдем положение первой главной площадки. Для этого используем первое уравнение системы

(0-s₁)×l₁ + 0 + t_zx×n₁ = 0.

Если обозначить через a₁ угол между нормалью n₁ и осью Х, то получим l₁ = cosa₁, n₁ = sina₁ и

-s₁×cosa₁ + t_zx×sina₁ = 0.

Откуда tga₁ = s₁/t_zx.

Из того же уравнения можно найти и положение третьей главной площадки

(0-s₃)×l₃ + t_zx×n₃ = 0.

Обозначив через точку b угол между нормалью и третьей главной площадкой и осью Х, получим

-s₃×cos b + t_zx×sin b = 0,

tgb = s₃/t_zx = s₃/t_zx.

Положительные углы a и b откладывать против часовой стрелки от оси Х.

Обобщенный закон Гука

Напряженное состояние в точке деформированного тела определяется составляющими по трем координатным площадкам s_х, s_у, s_z, t_xy, t_xz, t_yz. В той же точке деформированное состояние задается составляющими e_x, e_y, e_z,, g_ху, g_yz, g_zx, где e_x, e_y, e_z – линейные деформации в данной точке вдоль координатных осей; g_ху, g_yz, g_zx – угловые деформации или углы сдвига в координатных плоскостях.

На основании гипотезы об идеальной упругости материала детали связь между этими составляющими описывается следующими выражениями:

e_x = [s_x - m×(s_y +s_z)]/E,

e_y = [s_y - m×(s_x + s_z)]/E,

e_z = [s_z - m×(s_y + s_x)]/E,

g_xy = t_xy/G, g_zy = t_zy/G, g_xz = t_xz/G.

Эти шесть формул носят название обобщенного закона Гука для изотропного тела в общем случае трехосного напряженного состояния.

Упругие постоянные материала детали:

Е – модуль упругости первого рода или модуль Юнга,

G – модуль упругости второго рода или модуль сдвига,

m - коэффициент Пуассона.

Для стали можно считать

Е = 2×10¹¹ Па; G = 8×10¹⁰ Па; m = 0,3.