Стандартных распределений ДСВ

Закон распределения	Математическое ожидание	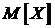Дисперсия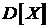
Биномиальный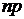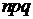
Закон Пуассона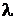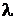
Геометрический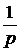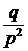
Гипергеометрический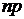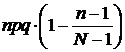

Пример.Вероятность попадания в цель при одном выстреле равна 0,01. Какова вероятность того, что число попаданий при 200 выстрелах составит не менее 5 и не более 10? Найти математическое ожидание и дисперсию случайной величины Х – числа попаданий в цель.

Решение.Вероятность 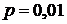очень мала, а число выстрелов (опытов) достаточно велико. Поэтому искомую вероятность будем находить, используя формулу Пуассона. Случайная величина Х – число попаданий в цель. Требуется найти 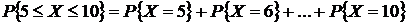. Имеем: ,

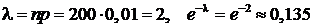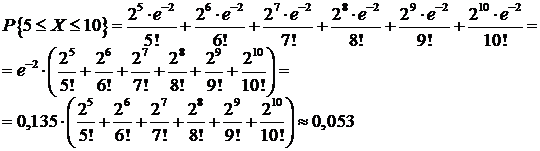
Искомая вероятность приближенно равна 0,053, а числовые характеристики данной случайной величины .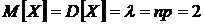

Пример. Вероятность попадания в цель при отдельном выстреле для данного стрелка равна 0,1. Найти математическое ожидание и дисперсию случайной величины 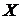– числа выстрелов по цели до первого попадания.

Решение.Случайная величина 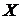имеет геометрическое распределение с параметром 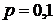. Тогда .

, .

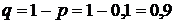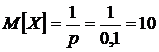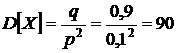Законы распределения непрерывных случайных величин

Равномерное распределение

Говорят, что случайная величина 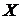имеет равномерное распределение на отрезке 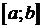, если ее плотность распределения имеет вид:

.

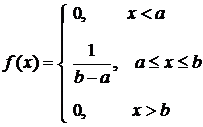Рис. 5. Кривая равномерного распределения

Функция распределения имеет вид:

.

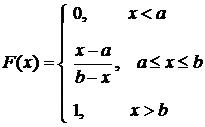Рис. 6. График функции равномерного распределения

Например, равномерное распределение присутствует при взвешивании на весах – ошибка взвешивания равномерно распределена в интервале .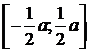

Пример.Цена деления шкалы амперметра равна 0,1 А. Показания округляют до ближайшего целого деления. Найти вероятность того, что при отсчете будет сделана ошибка, не превышающая 0,02 А.

Решение.Ошибку округления можно рассматривать как случайную величину Х, которая распределена равномерно в интервале между двумя соседними целыми делениями.

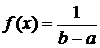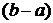Плотность равномерного распределения , где – длина интервала, в котором заключены возможные значения Х, вне этого интервала 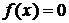. В данном случае длина интервала, в котором заключены возможные значения Х, равна 0,1, поэтому 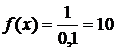, и

.

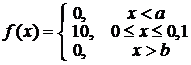Ошибка отсчета превысит 0,02, если она будет заключена в интервале (0,02; 0,08).

По формуле 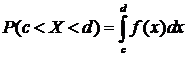получим:

.

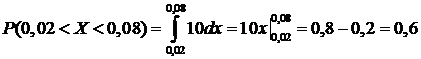Показательное распределение

Говорят, что случайная величина 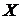имеет показательное распределение с параметром 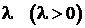, если ее плотность распределения имеет вид: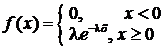

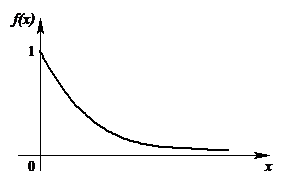Рис. 7. Кривая показательного распределения

Функция распределения имеет вид:

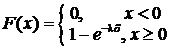
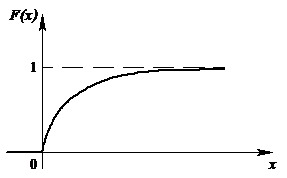Рис. 8. График функции показательного распределения

Показательное распределение является единственным абсолютно непрерывным распределением, для которого выполнено свойство «не старения» (и в этом смысле оно является непрерывным аналогом дискретного геометрического распределения).

В большинстве случаев время безотказной работы элемента, например электрической лампочки, распределено по показательному закону.

Пример.Непрерывная случайная величина Х распределена по показательному закону, заданному при 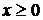плотностью распределения 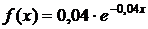; при 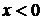функция 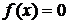. Найти вероятность того, что в результате испытания Х попадет в интервал .

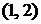Решение.Используем формулу .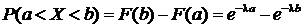

Учитывая, что по условию 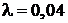, , 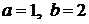получим:

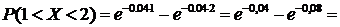0,961– 0,923=0,038.

Нормальное распределение

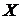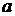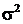Говорят, что случайная величина имеет нормальное распределение с параметрами и , где 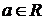, , 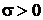если 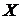имеет следующую плотность распределения: .

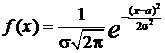Параметр 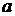есть математическое ожидание нормально распределенной случайной величины, 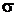– среднеквадратическое отклонение.

Кривая нормального распределения имеет вид (рис. 9):

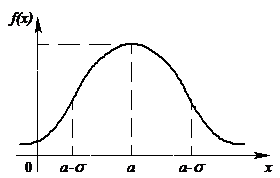Рис. 9. Кривая нормального распределения с параметрам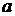и и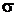

Нормальное (иначе называемое гауссовским по имени Карла Гаусса) распределение играет исключительно важную роль в теории вероятностей, поэтому мы очень подробно изучим все свойства этого распределения.