Методы решения транспортной задачи

I. Модификация симплекс-метода для решения транспортной задачи – распределительный метод.

Пусть имеем транспортную задачу общего вида:

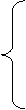
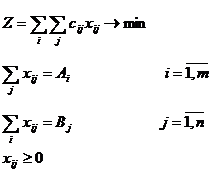
Рассмотрим ограничения задачи.

Общее число уравнений в ограничениях равно m+n. Это каноническая форма задачи. Но так как присутствует условие сбалансированности задачи 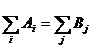, которое «связывает» некоторые переменные, то число линейно независимых уравнений будет m+n-1. Тогда, так как число неизвестных равно 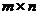, а число линейно независимых ограничений m+n-1 , то число базисных (ненулевых) переменных в невырожденном опорном плане будет m+n-1 - число положительных компонент (остальные будут нулевые).

Содержательно: имеем в невырожденном опорном плане m+n-1 ненулевую поставку, которые образуют суммарный объем перевозок со всех пунктов отправления во все пункты потребления.

Определение: Опорный план вырожденный, если он содержит число положительных компонент строго меньше, чем n+m-1.

Так как транспортная задача является задачей линейного программирования, то ее можно решить симплекс-методом. Однако, в силу специфики системы ограничений был разработан специальный метод и специальное представление структуры данных задачи, которые позволили решить задачу более простыми (по сравнению с таблицами) средствами.

1 шаг – построение исходной транспортной таблицы.

магазины   Базы	B1	B2	B3	B4	B5	Запасы
A1	5	0 3	6	5	300 3
A2	7	150 1	150 3	6	4
A3	250 2	0 4	5	150 2	7
Потребности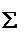

В уголках клеток ставим тарифы.

В таблицу заносят значения только ненулевых поставок и клетка таблицы с ненулевой поставкой x_ij>0 называется занятой, остальные – свободными, т.е. x_ij=0. Свободные клетки пустые.

Число итераций (шагов) в алгоритме при решении транспортной задачи существенно зависит от исходного опорного плана, который можно формировать несколькими методами.

Составление исходного опорного плана:

1) Метод северо-западного угла

Заполнение транспортной таблицы ненулевыми поставками начинается с верхнего левого угла и заканчивается нижним правым. При этом не учитывается значение тарифов.

2) Метод наименьшего элемента

а) по строкам

б) по столбцам

в) по всей таблице

Идея: По минимальному тарифу перевозится максимально возможное количество продуктов. Для этого выбирается клетка с наименьшим тарифом, и в эту клетку заносят поставку x_ij = (A_i, B_j).

Полученный исходный опорный план проверяется на вырожденность (число занятых клеток должно быть m+n-1).

Замечание: если число занятых клеток меньше, чем m+n-1, то обычно в клетки с минимальным тарифом ставят ноль и считают эти клетки занятыми, но это допустимо лишь том случае, если вновь образованные занятые клетки вместе с клетками плана не являются ациклическим набором занятых клеток, т.е. если занятые клетки не образуют цикла.

2 шаг – проверяем построенный невырожденный план на оптимальность.

Для этого вводится два понятия:

1) понятие цикла

2) оценки свободных клеток

Определение: Циклом (замкнутой цепью) клеток транспортной таблицы называют замкнутую ломаную линию, звенья которой взаимно перпендикулярны и проходят только вдоль строк и столбцов (последовательность клеток), удовлетворяющих следующим условиям:

1) Две и только две занятые клетки должны находиться в одном столбце и в одной строке, в которых данная линия осуществляет «поворот» на 90°.

2) Последняя занятая клетка цикла находится в одной строке или в одном столбце с первой клеткой цикла.

Определение: Клетки, в которых цикл осуществляет поворот, называются клетками цикла или вершинами. Так как цикл строится для свободной клетки, то клетками цикла будет одна свободная, остальные все - занятые.

3) Если ломаная линия, образующая цикл, самопересекается, то клетки самопересечения не являются клетками цикла. Если же цикл проходит через занятую клетку, но нет в ней поворота, то она тоже не является клеткой цикла.

При построении цикла руководствуются следующими правилами:

1) Никакая последовательность занятых клеток не образует цикла. Это является необходимым условием существования цикла.

2) Для каждой свободной клетки существует только единственный цикл.

Пусть для свободной клетки ij построен цикл. Тогда каждой клетке цикла соответствует определенный коэффициент целевой функции - c_ij. Расставим чередующиеся знаки – и +, начиная с – в свободной клетке, для которой этот цикл строится, и осуществим обход цикла (в любое направление), подсчитывая при этом алгебраическую сумму тарифов клеток цикла, которую назовем оценкой свободной клетки ij, и обозначим ее через ∆ _ij

Каждая такая оценка является элементом индексной строки исходной симплекс-таблицы, и так как число оценок совпадает с числом свободных клеток (аналог оценок небазисных векторов), то справедлива первая транспортная теорема:

Оценка свободной клетки ij есть ij-й элемент индексной строки симплексной таблицы и численно равна величине z_ij - c_ij.

Опираясь на эту теорему, формируется критерий оптимальности транспортной задачи, и т.к. это линейная задача на минимум, то справедлива следующая теорема.

План х^*_ij транспортной задачи является оптимальным, если все оценки свободных клеток не положительны.

Это критерий вырожденности (не единственности) оптимального плана. Если среди оценок свободных клеток есть не нулевые, то существует еще один оптимальный план (отличный от данного), значение целевой функции на котором такое же как и на данном оптимальном плане. Другой оптимальный план можно получить согласно второй транспортной теореме для свободной клетки с нулевой оценкой.

Если же план не оптимальный, то переход к новому опорному плану можно осуществить на основании второй транспортной теоремы.

Вторая транспортная теорема

Х – невырожденный опорный план, который не является оптимальным, т.е. среди свободных клеток есть положительные. Тогда:

1) среди положительных оценок свободных клеток выбираем наибольшее, и для этой клетки строим цикл, в котором выставляем чередующие знаки – и +, начиная со свободной клетки.

2) среди всех поставок положительных клеток цикла выбирается наименьшая, которая затем прибавляется к поставкам в отрицательных клетках цикла и вычитается из поставок положительных клеток цикла. В результате такого преобразования получаем новый опорный план, который может быть вырожденным (это возможно если наименьшая «положительная» поставка находится в двух или более клетках цикла). И тогда прежде чем проверять полученный план на оптимальность, его следует сделать не вырожденным.

Замечание: если клеток с наибольшей положительной оценкой несколько, то для каждой из них следует построить цикл, расставить знаки и определить величину минимальной положительной поставки. Выбираем клетку для перераспределения, для которой найденная положительная поставка цикла будет наибольшей, и именно по данному циклу осуществляем переход к новому опорному плану.