Специальные виды целочисленных задач.

Транспортная задача

1. Транспортная задача. Распределительный метод.

2. Метод потенциалов (Канторовича)

3. Задача о назначениях. Венгерский алгоритм.

Классическая транспортная задача – это задача о наиболее экономичном плане перевозок однородного (или взаимозаменяемых) продукта из заданных пунктов отправления (пункта производства или хранения) в пункты назначения (пункты потребления данного продукта). Наиболее часто встречается в распределительных экономических задачах.

Эта задача связана с территорией, распределением, назначениями, транспортом и размерами производства. Кроме того, различные варианты этой задачи встречаются в задачах организации производства, принятия решений и организационного управления.

Классическая подстановка: имеется m пунктов производства или складирования однородного продукта, запасы которого равны соответственно A₁…A_i….A_m. Имеется n пунктов потребления этого же продукта с потребностями В₁…В_j….В_n. Известны тарифы (транспортные расходы, связанные с доставкой единицы продукта из заданного пункта отправления в заданный пункт потребления)

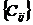
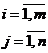
Требуется составить план перевозок (указать какое количество из какого пункта отправления и в какой пункт потребления следует перевезти продукт), обеспечивающий наиболее экономичным путем (при суммарных минимальных затратах на перевозку) удовлетворение всех пунктов потребления за счет реализации всего продукта, находящегося в пунктах отправления.

Фактически требуется указать вектор 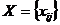поставок ( 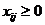), где x_ij – количество единиц продукта, направленного из i-го пункта отправления в j-й пункт потребления и удовлетворяющий следующим условиям:

1) Условие полного удовлетворения потребностей всех пунктов потребления.

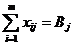
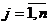
2) Весь продукт, хранимый на базах, должен быть вывезен.

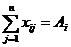
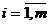
и дающий минимум целевой функции

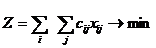
Транспортная задача исследуется только на минимум.

Определение: Транспортная задача называется закрытой (сбалансированной), если суммарный объем запасов равен суммарному объему потребностей:

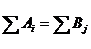
В противном случае она называется открытой.

Теорема 1 (необходимое условие разрешимости транспортной задачи)

Транспортная задача разрешима тогда и только тогда, когда она сбалансированная.

Если задача открытая, то ее всегда можно привести к закрытой, при этом следует произвести следующие преобразования:

а) Случай дефицита (суммарное потребление строго больше суммарных запасов). В этом случае вводят фиктивный пункт отправления с запасами, равными 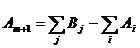, из которого перевозка во все пункты назначения осуществляется по нулевым тарифам.

б) Случай избытка продукта. Вводится фиктивный пункт потребления с потребностями 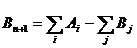, перевозки в который со всех пунктов отправления осуществляются по нулевым тарифам.