Основные свойства решения задач ЛП
Рассмотрим различные формы представления задачи линейного программирования:
1)  Векторная форма записи:
Векторная форма записи:
Z=CX®max
A1X1+…+AnXn 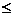 B
B
X 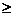 0
0
где C=(C1…Cn) – вектор коэффициента целевой функции (строка коэффициента);
X=(Х1…….Хn) – вектор-строка переменных задач;
CX – скалярное произведение векторов, равное сумме произведений их соответствующих компонентов,т.е. СХ = С1Х1 +….+ СnХn;
A1…An – векторы условий, но векторы-столбцы при соответствующих переменных;
B – вектор - столбец ограничения или вектор правых частей.
2)  Матричная форма
Матричная форма
Z=CX 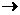 max
max
AX 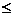 B
B
X 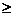 0
0
A – матрица условий, составленная из столбцов-векторов A1…An,
 |
X2
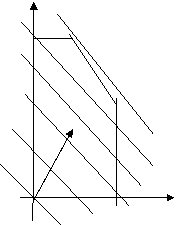
3)Геометрическая интерпретация
Z=C1X1+…..+CnXn 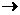 max
max
a1x1+….+an xn 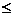 bi
bi
……………..
X1
Am 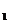 x1+……+amnxn
x1+……+amnxn 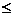 bm
bm
x1….. xn 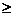 0
0
Геометрическую интерпретацию даем только в случае двух переменных. Тогда выражение Z=C1X1+C2X2 в зависимости от значения Z представляет собой семейство параллельных прямых, которые в точке (0,0) Z=0, и с увеличением Z прямые «приближаются» к границам области допустимых решений, которые определяются заданными неравенствами. Максимальное значение целевой функции достигается в одной (или нескольких) граничных точках области допустимых решений.
Необходимые сведения берутся из линейной алгебры.
Вектор – упорядоченный набор из n-действительных чисел, которые называются координатами вектора.
Векторы равны, когда они имеют одинаковую размерность и соответствующие координаты совпадают.
Вектор B , равный α1A1+…+αnAn, является линейной комбинацией векторов A1…An, если существуют такие числа a1…an, одновременно не равные нулю, при которых это равенство выполняется.
Система векторов A1…An называется линейно зависимой, если существуют такие числа a1,…,am 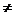 0(одновременно не равные нулю) и такие что выполняется равенство: (*) 0=a1A1+…amAm , где 0 – нуль-вектор (все его компоненты равны нулю).
0(одновременно не равные нулю) и такие что выполняется равенство: (*) 0=a1A1+…amAm , где 0 – нуль-вектор (все его компоненты равны нулю).
Через Rn обозначим множество всех векторов размерности n c операциями сложения векторов и умножения их на число. В дальнейшем рассмотрим только векторы одинаковой размерности.
Если равенство (*) выполняется только в случае, когда все a1,…an равны нулю, то система векторов A1…An линейно независима.
Содержательно: система векторов линейно независима, если никакой ее вектор нельзя представить в виде линейной комбинации остальных векторов системы.
Базис – максимально линейно-независимая система векторов в пространстве. Любой базис содержит в пространстве Rn n-векторов. Единичный базис – система, состоящая из n различных единичных векторов E1……En (i-й единичный вектор, у которого на i месте 1, а остальные компоненты равны 0).
Элементы выпуклого анализа.
Линейная комбинация векторов (*) R=a1A1+…+anAn называется выпуклой, если выполняется условие:
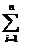 ai=1 и все ai неотрицательны.
ai=1 и все ai неотрицательны.
В двухмерном случае выпуклой комбинацией двух векторов (точек двухмерного пространства) есть отрезок, их соединяющий.
Определение: множество называется выпуклым, если вместе с каждой парой своих элементов, оно содержит все их выпуклые комбинации.
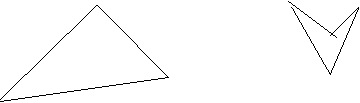
выпуклое невыпуклое
множество множество
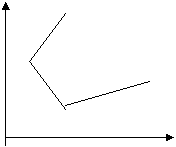
Система линейных неравенств в ограничениях задачи ЛП стандартной формы определяет некоторое выпуклое возможно неограниченное множество, которое называют многогранником решений.
 | |||
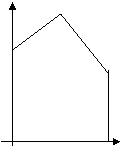 | |||
Ограниченный и Неограниченный
многогранники решения.
Определение: угловая точка многогранника решений – это такая точка многогранника, которая не является выпуклой линейной комбинацией никаких других точек многогранника (не лежит на отрезке, соединяющим две другие точки многогранника).
Если система ограничений содержит конечное число неравенств, то число угловых точек будет конечно и не превосходит С 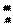 -числа сочетаний.
-числа сочетаний.
Теорема № 1.
