Теоретическая механика. Кинематика. Динамика. Механические передачи. Кинематические и динамические зависимости в передачах. Расчет привода.
Раздел 2. КИНЕМАТИКА
Этораздел теоретической механики, который изучает движение тел без учета действующих сил.
Тема 1.8 Основные понятия кинематики
Система отсчета – твердое тело, связанное с системой координат, с помощью которого определяется положение тела в пространстве.
Момент времениопределяет изменение положения тела с течением времени: t , t0 , ∆t .
Траектория точки –геометрическое место положений движущейся точки. В зависимости от формы траектории различают: - прямолинейное движение; - криволинейное движение.
Закон движенияопределяетположение движущейся точки в пространстве и во времени.
Способы задания движения точки: - естественный; - координатный.
Тема 1.9 Кинематика точки.Естественный способ задания движения.
Скорость материальной точки- есть вектор, характеризующий быстроту и направление перемещения материальной точки в данный момент времени, определяемый как первая производная перемещения по времени и проведенный касательно траектории движения ,м/с. В зависимости от скорости различают движения: равномерное; неравномерное.
,м/с. В зависимости от скорости различают движения: равномерное; неравномерное.
Ускорение материальной точки -есть вектор, характеризующий быстроту изменения скорости: 1) по величине α τ = υ΄ - касательное ускорение, направлено по касательной к траектории; 2) по направлению  - нормальное ускорение, направлено по радиусу кривизны к центру. В зависимости от касательного ускорения различают движения: ускоренное и замедленное.
- нормальное ускорение, направлено по радиусу кривизны к центру. В зависимости от касательного ускорения различают движения: ускоренное и замедленное.
Тема 1.10Простейшие движения твердого тела
Поступательное движение –движение, при котором любая прямая, связанная с телом перемещается параллельно самой себе.
Для этого движения S– перемещение, м; S = f(t) – закон движения; υ = S΄ -линейная скорость, м/с; α τ = υ΄-касательное ускорение, м/с2 ;  - нормальное ускорение, м/с2
- нормальное ускорение, м/с2
Вращательное движение– движение, при котором в теле имеется хотя бы две точки, скорость которых в данный момент времени равна нулю.
Для этого движения φ - угол поворота, рад; φ = f(t) - закон движения, ω - угловая скорость, рад/м; ε - угловое ускорение, рад/м2
Равномерное вращательное движение. Угловая скорость твердого тела:  , где n – частота вращения тела, об/мин. Линейная скорость любой точки твердого тела:
, где n – частота вращения тела, об/мин. Линейная скорость любой точки твердого тела:  , где d - диаметр тела вращения
, где d - диаметр тела вращения
Раздел 3. ДИНАМИКА
Этораздел теоретической механики, который изучает движение тел с учетом действующих сил.
Тема 1.13 Задачи и законы динамики
Первая задача - определить движущие силы по известному закону движения.
Вторая задача – обратная первой.
Закон инерции ( см. статику)
Основной закон динамики (второй закон Ньютона). Ускорение, сообщаемое материальной точке приложенной к ней силой, пропорционально модулю этой силы и совпадает с ней по направлению. Согласно этому закону, движущая сила F = mα, где m – масса материальной точки.
Закон равенства действия и противодействия (см. статику).
Закон независимости действия сил. Ускорение, получаемое материальной точкой при одновременном действии на нее нескольких сил, равно геометрической сумме тех ускорений, которые получила бы эта точка под действием каждой из данных сил в отдельности.
Тема 1.14 Движение материальной точки
Принцип кинетостатики.Всякое движущееся тело можно рассмотреть в состоянии условного равновесия, если добавить силу инерции. Т.е. остановить тело можно при помощи другого тела, согласно закону равенства действия и противодействия с помощью силы равной по величине и противоположной по направлению. Этой силой называется сила инерции. С применением этого принципа решаются задачи динамики.
Задача 9. Тело движется по выпуклой поверхности по закону S = 0,8 t. Вес тела G = 5 кН. Определить давление тела на выпуклую поверхность в момент прохождения через середину, если радиус кривизны R = 1 м.
1. Статическая часть – составить расчетную схему, указать активные и реактивные нагрузки.
2. Кинематическая часть – исследовать движение тела (определить скорость и ускорение).
3. Динамическая часть - применить принцип кинетостатики (добавить на расчетной схеме силу инерции, и составить уравнения равновесия)
Задача 10. Выполнить условие задачи 7, только при движении тела по вогнутой поверхности.
1. Статическая часть – составить расчетную схему, указать активные и реактивные нагрузки.
2. Кинематическая часть – исследовать движение тела (определить скорость и ускорение).
Аналогична части 2 задачи 7.
3. Динамическая часть - применить принцип кинетостатики (добавить на расчетной схеме силу инерции, и составить уравнения равновесия)
Вывод по задачам 9,10: При движении по вогнутой поверхности давление (нагрузки) на тело больше, поэтому рациональными считаются выпуклые траектории. А как необходимо двигаться по вогнутой поверхности, чтобы нагрузки на тело были меньше?
Тема 1.15Работа и мощность. КПД
Работазатрачивается механической характеристикой конкретного движения (силой или моментом) при перемещении тела на определенное расстояние. Мощностьесть работа, совершенная в единицу времени.  Вт.
Вт.
| Постутательное движение | Вращательное движение | |
| Закон движения | s = f(t) | φ = f(t) |
| Скорость | υ = s' | ω = φ' |
| Работа | W = Fs | W = Тω |
| Мощность | Р = Fυ | Р = Тω |
Примечание: Основным в передачах является вращательное движение, поэтому следует запомнить выделенную зависимость. Обратить внимание на Т в задаче 13.
Задача 11. Лента конвейера движется по закону S = 1,5t усилием F = 2 кН. Определить мощность, затрачиваемую на движение ленты.
Движение - . Скорость движения ленты
Мощность:
Задача 12. Определить мощность, необходимую для вращения тела диаметром d = 30 мм по закону φ = 4t, если окружная сила Ft = 1,5 кН.
Движение - . Скорость вращения тела
Мощность:
Задача 13. Определить и показать на расчетной схеме (рис.1) окружную силу для точки А тела диаметром d = 180 мм, передающего вращающий момент Т = 180 Нм.
Рис.1 Расчетная схема задачи 13
Задача 14. Вал диаметром d = 40 мм вращается с частотой n = 122 об/мин и передает вращающий момент Т = 100 Нм. Определить мощность на валу и линейную скорость точки А вала, и показать ее на расчетной схеме.
Движение -
Мощность –
Линейная скорость –
Расчетная схема -
Тема 1.16Общие сведения о передачах
Передача вращательного движения от одной машины к другой или внутри машины от одного вала к другому осуществляется разнообразными механизмами, носящими название передач. Вращательное движение получило наибольшее распространение в механизмах и машинах, так как обладает следующими достоинствами: 1. Обеспечивает непрерывное и равномерное движение при небольших потерях на трение; 2. Позволяет иметь простую и компактную конструкцию передаточного механизма.
Валы и закрепленные на них шкивы и колеса называются ведущими звеньями, когда они передают движение, и ведомыми, когда они его воспринимают.
Классификация передач:
1. По принципу передачи движения:
- передачи трением (фрикционная, ременная);
- передачи зацеплением (цепная, зубчатая, червячная, винт-гайка);
2. По способу соединения деталей
- передачи с непосредственным контактом тел вращения (фрикционная, зубчатая, червячная, винт-гайка);
- передачи с гибкой связью (ременная, цепная).
Основными характеристиками передачи являются передаточное отношение и КПД.
Передаточным отношением называется отношение угловых скоростей ведущего звена к ведомому :  . Если i<1 – передачи, повышающие ω, если i>1, то - понижающие ω.
. Если i<1 – передачи, повышающие ω, если i>1, то - понижающие ω.
Для передач трением - это отношение диаметров ведомого звена к ведущему:  ; для передач зацеплением – отношение чисел зубьев
; для передач зацеплением – отношение чисел зубьев  .
.
КПД характеризует степень совершенства механизма и определяется отношением мощностей ведомого звена к ведущему: 
Привод - это совокупность передач или многоступенчатая передача, ведущий вал которой получает движение от электродвигателя.
Передаточное отношение привода равно произведению передаточных отношений входящих передач:  .
.
КПД привода равно произведению КПД входящих передач: 
Варианты выполнения задач по расчету привода:
Вариант 1. Заданы параметры всех передач привода
Задача 15. Выполнить силовой и кинематический расчет привода (рис.1), если Pдв = 5 кВт, nдв = 980  , η31= 0,97, η32 = 0,98, ηЦ = 0,95 (КПД муфты и подшипников условно включены в КПД передач для упрощения решения задачи)
, η31= 0,97, η32 = 0,98, ηЦ = 0,95 (КПД муфты и подшипников условно включены в КПД передач для упрощения решения задачи)
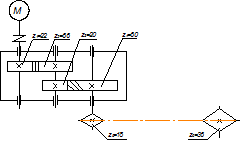
Рис.1 Схема привода
1.Дать характеристику привода.
Привод состоит из электродвигателя, цилиндрического двухступенчатого горизонтального редуктора (1 ступень – прямозубая передача, 2 ступень – косозубая передача) и цепной передачи.
2. Определить общий КПД привода.
η0 = η31 ∙ η32 ∙ ηЦ = 0,97 ∙ 0,98 ∙ 0,95 = 0,903
3.Определить общее передаточное отношение привода.
i0 = i31 ∙ i32 ∙ iЦ = 3 ∙ 3 ∙ 2 = 18
i31 = 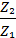 =
=  = 3 ; i32 =
= 3 ; i32 = 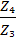 =
= 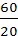 = 3 ;i ц =
= 3 ;i ц = 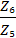 =
= 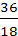 = 2
= 2
4. Определить угловые скорости всех валов привода.
ωдв = 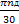 =
= 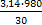 = 102,57
= 102,57 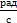
ω1 = ωдв = 102,57 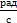 (соединение валов выполнено с помощью муфты, скорость не изменяется)
(соединение валов выполнено с помощью муфты, скорость не изменяется)
ω2 = 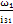 =
= 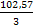 = 34,19
= 34,19 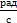
ω3 = 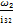 =
= 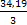 = 11,40
= 11,40 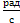
ω4 = 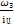 =
= 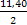 = 5,7
= 5,7 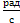
5. Определить мощности всех валов привода.
Рдв = 5 кВт
Р1= Рдв=5 кВт (КПД муфты не задано, поэтому мощность не изменяется)
Р2 = Р1∙η31= 5 ∙ 0,97 = 4,85 кВт
Р3 = Р2 ∙ η32 = 4,85 ∙ 0,98 = 4,75 кВт
Р4 = Р3 ∙ ηЦ = 4,75 ∙ 0,95 = 4,51 кВт
6. Определить вращающие моменты всех валов привода.
Тдв = 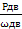 =
= 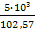 = 48,7 Нм
= 48,7 Нм
Т1 = 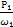 = Тдв = 48,7 Нм
= Тдв = 48,7 Нм
Т2 = 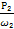 =
= 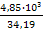 = 142 Нм
= 142 Нм
Т3 = 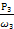 =
= 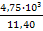 = 417 Нм
= 417 Нм
Т4 = 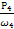 =
= 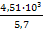 = 791 Нм
= 791 Нм
Вариант 2. Нет параметров одной из передач привода, но задана угловая скорость ωр.
Задача 16. Выполнить силовой и кинематический расчет привода (рис.1), если Рдв = 7,5 кВт, ωдв=150 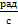 , ωр = 2,5
, ωр = 2,5 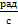 , ηр= 0,94, ηЗ1= 0,98, ηЗ2 = 0,98.
, ηр= 0,94, ηЗ1= 0,98, ηЗ2 = 0,98.
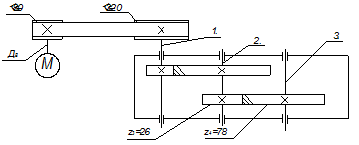
Рис.1 Схема привода
1. Дать характеристику привода.
Привод состоит из электродвигателя, ременной передачи и цилиндрического косозубого двухступенчатого горизонтального редуктора.
2. Определить общий КПД привода.
η0 = ηР ∙ η31 ∙ η32 = 0,94 ∙ 0,98 ∙ 0,98 = 0,903
3. Определить общее передаточное отношение привода.
Для данного варианта, когда нет параметров одной из передач, но задана угловая скорость на выходе из привода ωр, общее передаточное отношение привода определяется по формуле:
i0 = 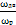 =
= 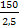 = 60 ,
= 60 ,
но для следующего пункта нужны передаточные отношения всех передач, поэтому:
ip = 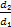 =
= 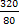 = 4
= 4
iЗ1 = 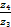 =
= 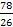 = 3
= 3
Так как i0 = ip ∙ iЗ1∙ iЗ2 , то iЗ1 = 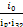 =
= 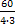 = 5
= 5
4. Определить угловые скорости всех валов привода.
ωдв=150 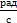
ω1 = 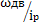 =
= 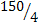 = 37,5
= 37,5 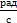
ω2 = 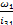 =
= 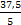 = 7,5
= 7,5 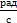
ω3 = 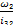 =
= 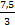 = 2,5
= 2,5 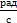
5. Определить мощности всех валов привода.
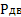 =7,5 кВт
=7,5 кВт
Р1 = Рдв∙ ηр = 7,5 ∙ 0,94 = 7,05 кВт
Р2 = Р1∙ ηЗ1 = 7,05 ∙0,98 = 6,91 кВт
Р3 = Р2∙ ηЗ2 = 6,91 ∙ 0,98 = 6,77 кВт
6. Определить вращающие моменты всех валов привода.
Тдв = 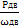 =
= 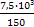 = 50 Нм
= 50 Нм
Т1 = 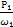 =
= 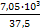 = 188 Нм
= 188 Нм
Т2 = 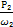 =
= 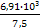 = 921 Нм
= 921 Нм
Т3 = 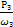 =
= 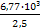 = 2710 Нм
= 2710 Нм
Задача 17. Выполнить силовой и кинематический расчет привода (рис.1), если Рдв = 5 кВт, ωдв = 150 рад\с, ηрем = 0,95, ηцил = 0,98, ηцеп = 0,92.
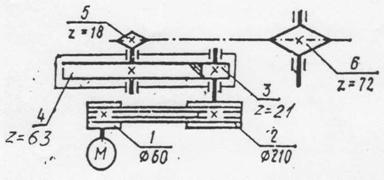 |
Рис.1 Схема привода
1. Дать характеристику привода.
Привод состоит из …
2. Определить общий КПД привода.
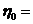
3. Определить общее передаточное отношение привода.
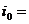
4. Определить угловые скорости всех валов привода.
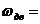
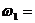
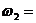
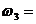
5.Определить мощности всех валов привода.
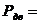

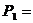
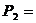
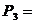
6. Определить вращающие моменты всех валов привода.
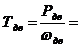
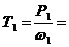
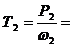
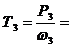
Задача 18. Выполнить силовой и кинематический расчет привода (рис.1), если Рдв = 10 кВт, ωдв = 102 рад\с , ηцеп = 0,92, ηз1 = 0,97, ηз2= 0,98.
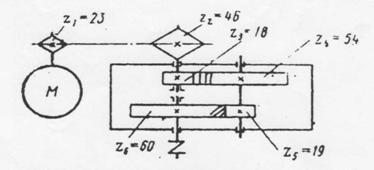 |
Рис.1 Схема привода
1. Дать характеристику привода.
Привод состоит из …
2. Определить общий КПД привода.
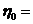
3. Определить общее передаточное отношение привода
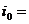
iцеп = iз1 = iз2 =
4. Определить угловые скорости всех валов привода.
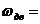
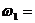
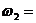
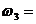
5.Определить мощности всех валов привода.
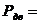

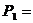
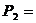
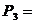
6. Определить вращающие моменты всех валов привода.
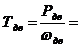
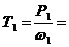
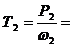
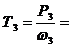
Задача 19. Выполнить силовой и кинематический расчет привода (рис.1), если Рдв = 4 кВт, nдв = 980 об\мин, 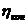 = 0,95 ,
= 0,95 , 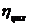 = 0,97,
= 0,97, 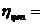 0,92.
0,92.
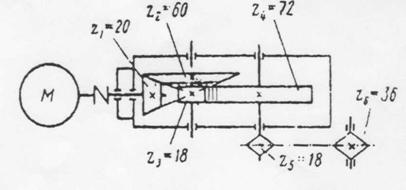 |
Рис.1 Схема привода
1. Дать характеристику привода.
Привод состоит из …
2. Определить общий КПД привода.
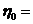
3. Определить общее передаточное отношение привода.
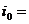
4. Определить угловые скорости всех валов привода.
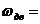
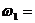
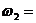
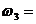
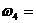
5.Определить мощности всех валов привода.
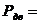
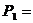
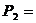
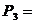
Р4 =
6. Определить вращающие моменты всех валов привода.
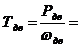
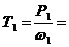
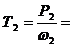
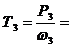
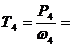
Задача 20. Выполнить силовой и кинематический расчет привода (рис.1), если Рдв = 12 кВт,
ωдв = 140 рад\с , η цил1= 0,98 , η цил2 = 0,98 , η кон = 0,92 , ωр = 4 рад\с.
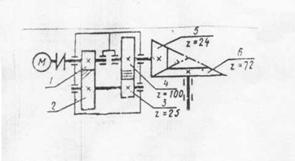
Рис.1 Схема привода
1. Дать характеристику привода.
Привод состоит из …
2. Определить общий КПД привода.
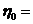
3. Определить общее передаточное отношение привода.
iо =
iцил1 = iцил2 = iкон =
4. Определить угловые скорости всех валов привода.
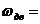
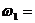
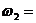
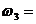
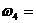
5.Определить мощности всех валов привода.
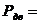

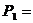
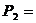
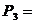
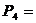
6. Определить вращающие моменты всех валов привода.
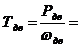
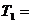
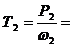
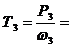
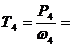
Задача 21 . Выполнить силовой и кинематический расчет привода (рис.1), если Рдв = 8 кВт, nдв = 1376 об\мин, η цил= 0,97, η кон = 0,96, η цеп = 0,92, ωр = 6 рад\с.
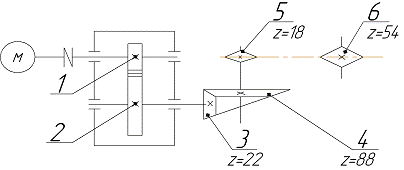
Рис.1 Схема привода
1. Дать характеристику привода.
Привод состоит из …
2. Определить общий КПД привода.
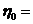
3. Определить общее передаточное отношение привода.
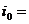
4. Определить угловые скорости всех валов привода.
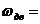
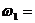
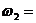
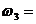
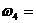
5. Определить мощности всех валов привода.
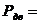

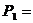
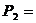
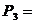
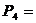
6. Определить вращающие моменты всех валов привода.
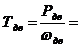
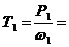
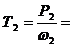
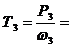
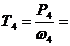
Задача 22 . Выполнить силовой и кинематический расчет привода (рис.1), если Рдв = 3 кВт, ωдв = 142 рад\с, η цеп = 0,95, η цил = 0,97, η кон = 0,96.
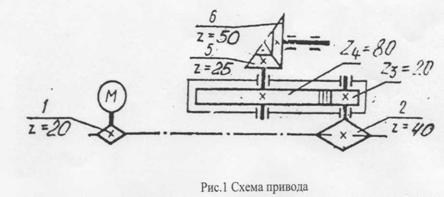 |
1. Дать характеристику привода.
Привод состоит из …
2. Определить общий КПД привода.
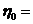
3. Определить общее передаточное отношение привода.
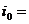
4. Определить угловые скорости всех валов привода.
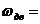
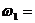
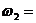
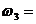
5. Определить мощности всех валов привода.
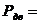
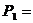
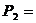
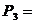
6. Определить вращающие моменты всех валов привода.
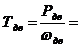
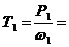
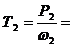
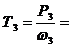
Задача 23 . Выполнить силовой и кинематический расчет привода (рис.1), если Рдв = 6 кВт, nдв = 975 об\мин, ηрем = 0,95, η кон = 0,96 , η цил = 0,97.
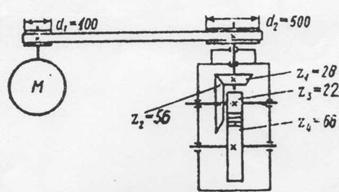 |
Рис.1 Схема привода
1. Дать характеристику привода.
Привод состоит из …
2. Определить общий КПД привода.
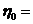
3. Определить общее передаточное отношение привода.
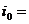
4. Определить угловые скорости всех валов привода.
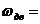
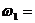
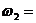
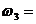
5. Определить мощности всех валов привода.
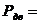

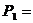
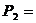
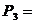
6. Определить вращающие моменты всех валов привода.
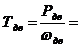
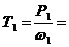
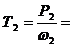
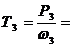
Часть 2. СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ
Тема 2.1 Основные положения сопротивления материалов
1. Задачи сопротивления материалов – Сопротивление материалов это наука которая рассматривает деформируемое тела, и дает основы расчетов элементов конструкций на прочность, жесткость и устойчивость.
2. Гипотезы и допущения сопротивления материалов:
– связанные со свойствами материалов – сплошность и однородность, изотропность, идеальная упругость;
- связанные с деформациями – линейность и малость деформаций, гипотеза плоских сечений, принцип независимости действия сил.
