Тема 1.3 Пара сил и момент силы

Пара сил (рис.1) - это система двух сил, параллельных, равных по модулю и противоположных по направлению. Оказывает на тело вращательное действие, которое характеризуется моментом пары.

m(F₁, F₂) = ± F_{1 *} h

Рис.1 К паре сил

Моментом пары называется взятое со знаком + или – произведение модуля одной из сил пары на плечо.Плечо h – это кратчайшее расстояние между линиями действия сил пары.

В системе СИ измеряется в Нм.

Правило знаков момента пары:

Момент пары положителен, если пара стремиться повернуть тело против часовой стрелки, и отрицателен, если - по часовой стрелке.

Свойства пары:

1.Пара сил не имеет равнодействующей. Уравновесить ее можно только противоположной парой.

2. Пара сил на ось не проецируется.

3. Не изменяя действия пары сил на тело, ее можно переносить в плоскости ее действия в любое место, поворачивать на любой угол, менять плечо и силы пары, оставляя при этом неизменным момент пары.

4. Чтобы задать пару, достаточно задать ее момент, поэтому слово «пара» заменяют словом «момент», и изображают ее дугой со стрелкой.

Теорема о сложении пар(без вывода): Система пар сил эквивалентна результирующей паре, момент которой равен алгебраической сумме моментов составляющих пар М_рез.= 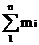Условие равновесия системы пар сил: М_рез.= 0.Момент результирующей пары равен нулю. Уравнение равновесия пар: 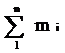=0.Для равновесия системы пар сил необходимо и достаточно, чтобы алгебраическая сумма моментов составляющих пар была равна нулю.

Момент силы относительно точки - это произведение модуля силы на плечо (рис.2). Плечо - это кратчайшее расстояние между точкой и линией действия силы.

M₀(F) = F h,Hм

Рис.2К моменту силы относительно точки

Правило знаков момента силы:

«+» , если сила стремится повернуть тело против часовой стрелки;

«- » , если сила стремится повернуть тело по часовой стрелке.

Тема 1.4 Плоская система произвольно расположенных сил (ПСПРС)

Это система сил, линии действия которых лежат в одной плоскости, и не пересекаются в одной точке. Данная система сил эквивалентна главному вектору и главному моменту.

Параллельный перенос силы(Теорема Пуансо). Механическое состояние твердого тела не нарушится, если силу перенести параллельно самой себе в произвольную точку тела, добавив при этом пару сил, момент которой равен моменту переносимой силы относительно произвольной точки (рис.1)

Рис. 1 К теореме Пуансо

Приведение ПСПРС к центру

Рис. 2 К приведению ПСПРС к центру

Главный вектор R_о ПСПРС равен геометрической сумме составляющих сил системы и приложен в центре приведения (рис.2). После приведения - это равнодействующая ПССС, поэтому модуль определяется по формуле: R_о= 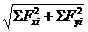, а направление по направляющему косинусу 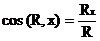. Главный момент М_о ПСПРС равен алгебраической сумме моментов составляющих сил относительно центра приведения. После приведения - это момент приведенной системы пар сил М _о = М_рез.=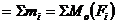

Условие равновесия ПСПРС: R = 0, М ₀ = 0. Главный вектор и главный момент равны нулю.

Зная, как определяются главный вектор и главный момент, имеемуравнения равновесия:

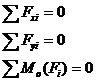- Уравнения равновесия (форма 1равновесия)

Для равновесия ПСПРС необходимо и достаточно, чтобы алгебраические суммы проекций составляющих сил на координатные оси плоскости и алгебраическая сумма моментов составляющих сил относительно произвольной точки плоскости были порознь равны нулю.

Для системы параллельных сил (это частный случай ПСПРС) существует вторая форма:

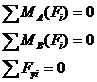- Уравнения равновесия (форма 2 равновесия)

Для равновесия системы параллельных сил необходимо и достаточно, чтобы алгебраические суммы моментов составляющих сил относительно двух произвольных точек плоскости и алгебраическая сумма проекций составляющих сил на координатную ось, не совпадающую с данными точками плоскости, были порознь равны нулю.