Алгоритм кнута-морриса-пратта (кмп)

Введем понятие префикс-функции. Префикс-функция для i-ой позиции — это длина максимального префикса строки, который короче i и который совпадает с суффиксом префикса длины i. Если определение Z-функции не сразило оппонента наповал, то уж этим комбо вам точно удастся поставить его на место :) А на человеческом языке это выглядит так: берем каждый возможный префикс строки и смотрим самое длинное совпадение начала с концом префикса (не учитывая тривиальное совпадение самого с собой). Вот пример для «ababcaba»:

префикс	префикс	p
a	a
ab	ab
aba	aba
abab	abab
ababc	ababc
ababca	ababca
ababcab	ababcab
ababcaba	ababcaba

Самое первое значение префикс-функции, очевидно, 0. Пусть мы посчитали префикс-функцию до i-ой позиции включительно. Рассмотрим i+1-ый символ. Если значение префикс-функции в i-й позиции P_i, то значит префикс A[..P_i] совпадает с подстрокой A[i-P_i+1..i]. Если символ A[P_i+1] совпадет с A[i+1], то можем спокойно записать, что P_i+1=P_i+1. Но вот если нет, то значение может быть либо меньше, либо такое же. Конечно, при P_i=0 сильно некуда уменьшаться, так что в этом случае P_i+1=0. Допустим, что P_i>0. Тогда есть в строке префикс A[..P_i], который эквивалентен подстроке A[i-P_i+1..i]. Искомая префикс-функция формируется в пределах этих эквивалентных участков плюс обрабатываемый символ, а значит нам можно забыть о всей строке после префикса и оставить только данный префикс и i+1-ый символ — ситуация будет идентичной.

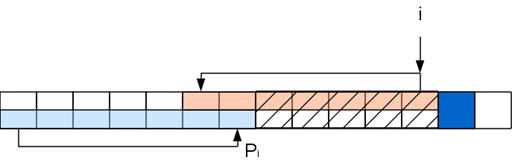
Задача на данном шаге свелась к задаче для строки с вырезанной серединкой: A[..P_i]A[i+1], которую можно решать рекурсивно таким же способом (хотя хвостовая рекурсия и не рекурсия вовсе, а цикл). То есть если A[P_Pi+1] совпадет с A[i+1], то P_i+1=P_Pi+1, а иначе снова выкидываем из рассмотрения часть строки и т.д. Повторяем процедуру пока не найдем совпадение либо не дойдем до 0.

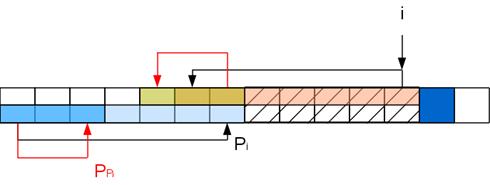
Повторение этих операций должно насторожить — казалось бы получается два вложенных цикла. Но это не так. Дело в том, что вложенный цикл длиной в k итераций уменьшает префикс-функцию в i+1-й позиции хотя бы на k-1, а для того, чтобы нарастить префикс-функцию до такого значения, нужно хотя бы k-1 раз успешно сопоставить буквы, обработав k-1 символов. То есть длина цикла соответствует промежутку между выполнением таких циклов и поэтому сложность алгоритма по прежнему линейна по длине обрабатываемой строки. С памятью тут такая-же ситуация, как и с Z-функцией — линейная по длине строки, но есть способ сэкономить. Кроме этого есть удобный факт, что символы обрабатываются последовательно, то есть мы не обязаны обрабатывать всю строку, если первое вхождение мы уже получили.
prefFunction(_pattern.size()), pattern(_pattern)

{

prefFunction[0] = 0;

long long q = 0;

for (size_t i = 1; i < pattern.size(); i++)

{

while (q > 0 && pattern[i] != pattern[q])

q = prefFunction[q - 1];

if (pattern[i] == pattern[q])

q++;

prefFunction[i] = q;

}

}

Алгоритм КМП осуществляет поиск подстроки в строке.
Условия:
Даны образец 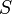и строка 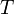. Требуется определить индекс, начиная с которого строка 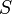содержится в строке 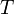. Если 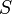не содержится в 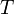— вернуть индекс, который не может быть интерпретирован как позиция в строке (например, отрицательное число). При необходимости отслеживать каждое вхождение образца в текст имеет смысл завести дополнительную функцию, вызываемую при каждом обнаружении образца.

Алгоритм:
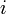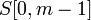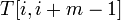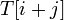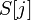Рассмотрим сравнение строк на позиции , где образец сопоставляется с частью текста . Предположим, что первое несовпадение произошло между и , где 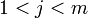. Тогда 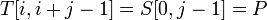и .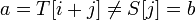
При сдвиге вполне можно ожидать, что префикс (начальные символы) образца 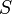сойдется с каким-нибудь суффиксом (конечные символы) текста 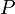. Длина наиболее длинного префикса, являющегося одновременно суффиксом, есть префикс-функция от строки 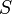для индекса .
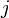Это приводит нас к следующему алгоритму: пусть 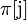— префикс-функция от строки 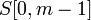для индекса 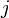. Тогда после сдвига мы можем возобновить сравнения с места 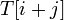и 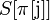без потери возможного местонахождения образца.

std::vector<long long>FindEntries(const std::string& text) const

{

std::vector<long long> answer;

long long q = 0;

for (size_t i = 0; i < text.size(); i++)

{

while (q > 0 && text[i] != pattern[q])

q = prefFunction[q - 1];

if (text[i] == pattern[q])

q++;

if (q == pattern.size())

{

answer.push_back(i - q + 2);

q = prefFunction[q - 1];

}

}

returnanswer;

}

Время работы

Время работы алгоритма составит 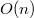. Для доказательства этого нужно заметить, что итоговое количество итераций цикла 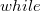определяет асимптотику алгоритма. Теперь стоит отметить, что 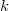увеличивается на каждом шаге не более чем на единицу, значит максимально возможное значение 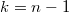. Поскольку внутри цикла 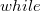значение 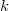лишь уменьшается, получается, что 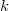не может суммарно уменьшиться больше, чем 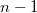раз. Значит цикл 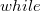в итоге выполнится не более 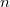раз, что дает итоговую оценку времени алгоритма .

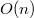Алгоритм Ахо-Корасика.

В задаче точного сопоставления множеств (exact set matching problem) требуется обнаружить все появления шаблонов из множества P = {P₁,...,P_k} в тексте T[1..m].
Пусть n = Σ_i=1^k |P_i|.
Задача точного сопоставления множеств может быть решена за время
O (|P₁| + m + ... + |P_k| + m) = O (n + km),
если применить k раз любой алгоритм, работающий за линейное время.
Алгоритм Ахо-Корасик (АК) (Aho-Corasick algorithm) (AC) - классическое решение задачи точного сопоставления множеств. Он работает за время O (n + m + z) , где z - количество появлений шаблонов в T.
АК основан на структуре данных "дерево ключевых слов" (keyword tree).

Дерево ключевых слов (бор)

Дерево ключевых слов (или "бор") (keyword tree, trie) для множества шаблонов P - это дерево с корнем K, такое что:
1. Каждое ребро e в K отмечено одним символом.
2. Всякие два ребра, исходящие из одной вершины, имеют разные метки.
Определим метку вершины v как конкатенацию меток ребер, составляющих путь из корня в v, и обозначим ее L (v).
3. Для каждого шаблона P_i из множества P есть вершина v, такая что L (v) = P_i.
4. Метка каждой вершины-листа является шаблоном из множества P.

Пример дерева ключевых слов (бора)

Дерево ключевых слов для P = {he, she, his, hers}:

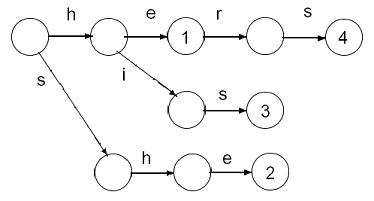
Бор - хороший способ хранения словаря строк.

Построение бора

Начинаем с дерева из одной вершины (корня); добавляем шаблоны P_i один за другим:
Следуем из корня по ребрам, отмеченным буквами из P_i, пока возможно.
Если P_i заканчивается в v, сохраняем идентификатор P_i (например, i) в v.
Если ребра, отмеченного очередной буквой P_i нет, то создаем новые ребра и вершины для всех оставшихся символов P_i.
Это занимает, очевидно, O (|P₁| + ... + |P_k|) = O (n) времени.

Поиск строки в бору

Поиск строки S в бору: начинаем в корне, идем по ребрам, отмеченным символами S, пока возможно.
Если с последним символом S мы приходим в вершину с сохраненным идентификатором, то S - слово из словаря.
Если в какой-то момент ребра, отмеченного нужным символом, не находится, то строки S в словаре нет.
Ясно, что это занимает O (|S|) времени. Таким образом, бор - это эффективный способ хранить словарь и искать в нем слова.
Теперь перейдем от бора к автомату (automaton), чтобы добиться поиска шаблонов в тексте за линейное время.

Автомат Ахо-Корасик

Состояния: узлы бора.
Начальное состояние: корень, обозначим его 0.
Действия автомата определяются тремя функциями, определенными для всех состояний:
1. Функция goto g (s, a) указывает, в какое состояние переходить из данного состояния s при просмотре символа a.
Если ребро (u, v) отмечено символом a, то g (u, a) = v;
g (0, a) = 0 для всех символов a, которыми не отмечено ни одно ребро, выходящее из корня.
~>Автомат остается в корне, пока просматриваются побочные символы.
При всех остальных аргументах g пусть выдает -1.
2. Функция неудачи f (s) указывает, в какое состояние переходить при просмотре неподходящего символа.
Рассмотрим метку вершины s и найдем самый длинный суффикс этой метки, такой, что с него начинается некоторый шаблон из множества P. Тогда f (s) пусть указывает на вершину, метка которой - этот суффикс.
3. Выходная функция out (s) выдает множество шаблонов, которые обнаруживаются при переходе в состояние s.

Пример автомата АК

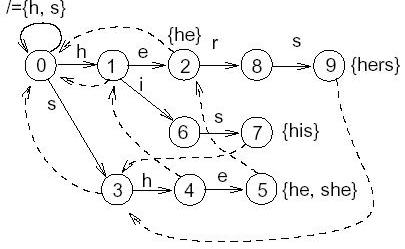
Пунктиром обозначены переходы при неудаче (значения функции f); те, которые не показаны, ведут в корень.