Флойд-Уоршалл (Floyd-Warshall)

Вход: взвешенный орграф
Выход: матрица длин кратчайших путей.
Алгоритм:
For v = 1 to V

For i = 1 to V

For j = 1 to V

Table[ i ][ j ] = min (Table[ i ][ j ], Table[ i ][ v ] + Table[ v ][ j ]);

Сложность: O(|V|^3)

Док-во корректности:

Ключевая идея алгоритма — разбиение процесса поиска кратчайших путей на фазы.

Перед 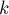-ой фазой ( 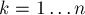) считается, что в матрице расстояний 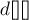сохранены длины таких кратчайших путей, которые содержат в качестве внутренних вершин только вершины из множества 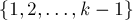(вершины графа мы нумеруем, начиная с единицы).

Иными словами, перед 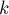-ой фазой величина 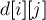равна длине кратчайшего пути из вершины 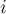в вершину 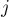, если этому пути разрешается заходить только в вершины с номерами, меньшими 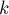(начало и конец пути не считаются).

Легко убедиться, что чтобы это свойство выполнилось для первой фазы, достаточно в матрицу расстояний 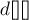записать матрицу смежности графа: 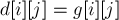— стоимости ребра из вершины 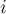в вершину 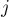. При этом, если между какими-то вершинами ребра нет, то записать следует величину "бесконечность" 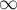. Из вершины в саму себя всегда следует записывать величину 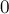, это критично для алгоритма.

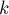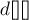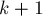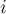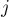Пусть теперь мы находимся на -ой фазе, и хотим пересчитать матрицу таким образом, чтобы она соответствовала требованиям уже для -ой фазы. Зафиксируем какие-то вершины и . У нас возникает два принципиально разных случая:

· Кратчайший путь из вершины 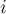в вершину 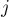, которому разрешено дополнительно проходить через вершины 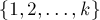, совпадает с кратчайшим путём, которому разрешено проходить через вершины множества .

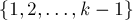В этом случае величина 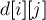не изменится при переходе с 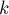-ой на 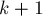-ую фазу.

· "Новый" кратчайший путь стал лучше "старого" пути.

Это означает, что "новый" кратчайший путь проходит через вершину 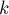. Сразу отметим, что мы не потеряем общности, рассматривая далее только простые пути (т.е. пути, не проходящие по какой-то вершине дважды).

Тогда заметим, что если мы разобьём этот "новый" путь вершиной 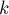на две половинки (одна идущая 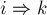, а другая — 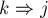), то каждая из этих половинок уже не заходит в вершину 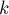. Но тогда получается, что длина каждой из этих половинок была посчитана ещё на 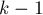-ой фазе или ещё раньше, и нам достаточно взять просто сумму 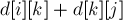, она и даст длину "нового" кратчайшего пути.

Объединяя эти два случая, получаем, что на 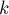-ой фазе требуется пересчитать длины кратчайших путей между всеми парами вершин 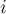и 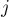следующим образом:

new_d[i][j] = min (d[i][j], d[i][k] + d[k][j]);

Таким образом, вся работа, которую требуется произвести на 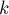-ой фазе — это перебрать все пары вершин и пересчитать длину кратчайшего пути между ними. В результате после выполнения 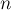-ой фазы в матрице расстояний 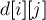будет записана длина кратчайшего пути между 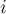и 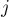, либо 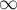, если пути между этими вершинами не существует.

Последнее замечание, которое следует сделать, — то, что можно не создавать отдельную матрицу 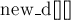для временной матрицы кратчайших путей на 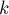-ой фазе: все изменения можно делать сразу в матрице 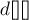. В самом деле, если мы улучшили (уменьшили) какое-то значение в матрице расстояний, мы не могли ухудшить тем самым длину кратчайшего пути для каких-то других пар вершин, обработанных позднее.

Асимптотика алгоритма, очевидно, составляет .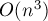

Алгоритм A*. Эвристики.

Алгоритм поиска А*

Находит маршрут с наименьшей стоимостью от одной вершины (начальной) к другой (конечной) с использованием эвристической функцией.
Вход: взвешенный граф, начальная вершина, конечная вершина.
Выход: последовательность вершин от начальной вершины до конечной.
Алгоритм: в каждой вершине есть поля h(x) - допустимая эвристическая оценка до конечной вершины (не превышает реального расстояния), g(x) - стоимость пути он начальной вершины, f(x) = g(x) + h(x). Алгоритм пошагово просматривает все пути, ведущие от начальной вершины в конечную, пока не найдет минимальный. В первую очередь он просматривает то алгоритмы, которые “кажутся” ведущими к цели, основываясь на значении функции f(x). В начале работы просматриваются вершины, смежные с данной, из них выбирается с минимальным значением f(x), после чего этот узел “закрывается” (помещается в множество “закрытых вершин”). На каждом этапе алгоритм работает с множеством “открытых вершин” (еще не пройденных), которые помещаются в очередь с приоритетом (приоритет по значению f(x)). Алгоритм продолжает свою работу до тех пор, пока значение f(x) целевой вершины не окажется меньшим, чем любое значение в очереди (либо пока всё дерево не будет просмотрено). Из множественных решений выбирается решение с наименьшей стоимостью.

Требования для эвристики (оценки)

1. h(u,t) <= b(u,t) – кратчайшее расстояние

2. h(a,c) <= h(a,b) + h(b,c)

Если сделать f(x) = g(x) – это Дейкстра.

Если всем вершинам сделать одинаковые, большие веса, а при доставании вершины из очереди уменьшать на 1 приоритет соседей – то будет BFS

Эвристики:

Поведение алгоритма сильно зависит от того, какая эвристика используется. В свою очередь, выбор эвристики зависит от постановки задачи. Часто А* используется для моделирования перемещения по поверхности, покрытой координатной сеткой.

§ Если мы можем перемещаться в четырех направлениях, в качестве эвристики стоит выбрать манхэттенское расстояние
.

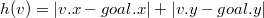§ Расстояние Чебышева применяется когда к четырем направлениям добавляются диагонали:
.

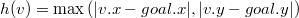§ Если передвижение не ограниченно сеткой, то можно использовать евклидово расстояние по прямой:
.

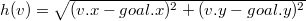Также стоит обратить внимание на то как соотносятся 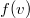и 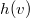. Если они измеряются в разных величинах (например, 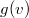— это расстояние в километрах, а 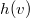— оценка времени пути в часах) А* может выдать некорректный результат.

Псевдокод:
OPEN = priority queue containing START
CLOSED = empty set
while lowest rank in OPEN is not the GOAL:
current = remove lowest rank item from OPEN
add current to CLOSED
for neighbors of current:
cost = g(current) + movementcost(current, neighbor)
if neighbor in OPEN and cost less than g(neighbor):
remove neighbor from OPEN, because new path is better
if neighbor not in OPEN and neighbor not in CLOSED:
set g(neighbor) to cost
add neighbor to OPEN
set priority queue rank to g(neighbor) + h(neighbor)
set neighbor's parent to current

reconstruct reverse path from goal to start
by following parent pointers

Если пишем пятнашки: