Поиск кратчайших путей в графе. Алгоритм Флойда. Алгоритм Дейкстры. Алгоритм Форда-Беллмана.

Вес пути – сумма весов ребер, входящих в путь

Вес кратчайшего пути из u в v (b(u,v)) – минимальный по длине путь из u в v, если он существует. Иначе – бесконечность

Кратчайший путь из u вv – путь из u в v, имеющий вес равный b(u,v) (т.к. может быть несколько кратчайших путей)

Задачи по поиску кр. путей:

1) P(u,v)? – Решаем, сводясь к 2 пункту (более быстрого алгоритма не существует)

2) P(u, v[i]) для всех I – Дейсктра, Форд-Беллман

3) Кратчайшие пути из всех вершин во все – Форд-Уоршелл

Свойства релаксаций:

ЛеммаP = <V1…Vk> - кратчайший путь из 1 в k. Тогда Pij = <Vj…Vj> - кратчайший путь между I и j.

Док-во: Если Pij – не кратчайший, то заменив в P этот участок более коротким путем – уменьшим вес пути P – противоречие.

Вес цикла может быть > 0, < 0 и равным 0

1) Если < 0 – то кратчайший путь уйдет по нему – поэтому Дейкстра не работает если есть цикл отрицательного веса (в отличии от Форда-Белммана)

2) Если > 0 – то он не войдет в кратчайший путь

3) Если == 0 – не имеет смысла ведь, но чтобы не было проблем:

Определения:

|P1k| <= |V| - 1

d[v] – массив кратчайших путей (текущий кратчайший путь из s)

Pi[v] – вершина-родитель в кратчайшем пути

Граф G(Pi) = (V(Pi), E(Pi))

V(Pi) = {v | Pi[v] != NULL} и s – стартовая вершина

E(Pi) = { (Pi[v], v) | v из V(Pi) \ {s}}

Дерево кратчайших путей – ориент подграф G’, что:

1) V’ – множество вершин, достижимых из s

2) S – корень, а G’ - дерево

3) Для каждой вершины v путь из s в v в G’ – кратчайший пусть из s в vвG

Relax(u,v,w)

{

If (d[v] > d[u] + w(u,v))

Then

d[v] = d[u] + w(u,v)

Pi[v] = u

}

b(s,v) – длина кратчайшего пути из s в v

Утверждения:

0) d[v] >=b(s,v)

1) b(s,v) <= b(s,u) + w(u,v)

2) Если нет пути из s в v – d[v] = b(s,v) = inf

3) Если есть путь s->u, и u->v, и u->v – кратчайший, а d[u] = b(s,u) до релаксации, то после нее – d[v] = b(s,v)

4) Есть путь P = <V₀,..,V_k>. Релаксация шла в порядке (V₀,V₁), (V₁,V₂) и т.д

Тогда d[V_k] = b(s, V_k)

5) Если v из V и d[v] = b(s,v), то подграф G(Pi) – дерево кратчайших путей с корнем s

Доказательства:

0) От противного

1) Вес кратчайшего пути из s в v<= весу любого пути из s в v, в том числе, и проходящего на последнем шаге через u

2) Очевидно

3) Из s->u – кратчайший

d[v] <= d[u] + w(u,v) = b(s,u) + w(u,v) = b(s,v) (т.к. s->u->v - кратчайший)

4) Вытекает из 3-его пункта

5) Следует из 0-4

Решение задачи P(u, v[i]) для всех i:

Через TopSort

1) TopSort(G)

2) Init

3) Перебор вершин в порядке сортировки:

Для всех v из Adj(u)

Relax(u,v,W)

Сложность: O(|E|*|V| + DFS(G)) – вроде

Дейкстра (Dijkstra)

Вход: взвешенный граф (веса положительны), стартовая вершина
Выход: вектор расстояний до стартовой вершины (опционально - вектор предков, чтобы восстановить кратчайший путь)
Алгоритм:

Проставляем расстояния: для стартовой 0, для остальных inf

Пусть PQ – очередь с приоритетом. PQ->push(s)

While(!PQ.empty())

u = PQ.ExtractMin();

u->color = Black;

for v из Adj(u)

If(v->color == WHITE)

d[v] = w(u,v) + d[u]

PQ.push(v)

v->color = Grey

else if v->color == Grey

if (d[v] > d[u] + w(u,v))

PQ.decreaseKey(v, d[u] + w(u,v) )

Сложность алгоритма Дейкстры зависит от способа нахождения вершины v, а также способа хранения множества непосещенных вершин и способа обновления меток. Обозначим черезn количество вершин, а через m — количество ребер в графе G.

· В простейшем случае, когда для поиска вершины сминимальным d[v] просматривается все множество вершин, а для хранения величин d используется массив, время работы алгоритма есть 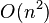. Основной цикл выполняется порядка n раз, в каждом из них на нахождение минимума тратится порядка n операций. На циклы по соседям каждой посещаемой вершины тратится количество операций, пропорциональное количеству рёбер m (поскольку каждое ребро встречается в этих циклах ровно дважды и требует константное число операций). Таким образом, общее время работы алгоритма 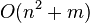, но, так как 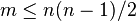, оно составляет .

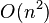· Для разреженных графов (то есть таких, для которых m много меньше n²) непосещенные вершины можно хранить в двоичной куче, а в качестве ключа использовать значения d[i], тогда время удаления вершины из 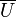станет 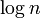, при том, что время модификации 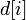возрастет до 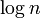. Так как цикл выполняется порядка n раз, а количество релаксаций (смен меток) не больше m, скорость работы такой реализации .

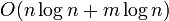· Если для хранения непосещенных вершин использовать фибоначчиеву кучу, для которой удаление происходит в среднем за 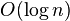, а уменьшение значения в среднем за 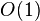, то время работы алгоритма составит .

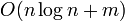Доказательство корректности Дейкстры:

Инвариант – для вершины, вытащенной из очереди уже нашли кр. путь (d[v] = b(s,v))

Это верно для любой вершины из S (множество вершин, для которых b(s,v) уже найдено – были вытащены из PQ)

0) S = пустое – для него верно

1) пусть u из S. От противного: d[u] != b(s,u), т.е. d[u] >b(s,u)

Пусть P – кратчайший путь из s в u

s->x->y->u, x из S, а y – еще не из S. u – первая вершина, для которой условие не выполняется

Утверждение:

d[y] = b(s,y)

d[x] = b(S,x) – верно, т.к. х из S (u – первая вершина с неверным условием)

при добавлении u в S - мы релаксируем (x,y) èd[y] = b(s,y)ЧТД

b(s,y) <= b(s,u) – очевидно

Значит d[y] = b(s,y) <= b(s,u) <= d[u] <= d[y], т.к. u – первая вершина с неверным условием, а мы вытащили u – т.е. ее приоритет ниже чем приоритет yèd[u] <= d[y]

Но тогда противоречие с d[u] >b(s,u).чтд

Алгоритм Белмана-Форда:

Алгоритм поиска кратчайшего пути во взвешенном графе
Условие: взвешенный граф, можно с отрицательными весами и циклами (с добавлением дополнительной проверки), стартовая вершина.
Алгоритм (без отрицательных циклов):

Для всех вершин проставляем расстояние = inf

Для начальной вершины расстояние = 0

For i = 1 to (V - 1)

Для всех ребер (u ,v)

Еслиd[v] >d[u] + w(u, v)

D[v] =d[u] + w(u, v)

Возвращаем вектор расстояний

Алгоритм (c отрицательными циклами):
Алгоритм Беллмана–Форда позволяет очень просто определить, существует ли в графе G отрицательный цикл, достижимый из вершины s. Достаточно произвести внешнюю итерацию цикла не 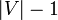, a ровно |V| раз. Если при исполнении последней итерации длина кратчайшего пути до какой-либо вершины строго уменьшилась, то в графе есть отрицательный цикл, достижимый из s. На основе этого можно предложить следующую оптимизацию: отслеживать изменения в графе и, как только они закончатся, сделать выход из цикла (дальнейшие итерации будут бессмысленны).
Сложность; O(|E|*|V|)

Доказательство корректности:

Утверждение:G – без циклов с отриц весом. Для всех достижимых вершин v из s – d[v] = b(s,v) после алг БФ

Док-во:

Рассмотрим v – достижима из s.

P = <V₀,…,V_k> - кратчайший ацикличный путь из s в v.

|P| <=|V| - 1 (ацикличный)

Во время i-ой итерации рассматриваем ребро (Vi-1, Vi).

d[v] = d[V_k] = b(s,V_k) = b(s,v). Если v – недостижима – d[v] = inf
Иначе d[v] <inf. Чтд

Утверждение – код - Алгоритм (c отрицательными циклами) корректен:

А) Нет цикла с отриц. весом

d[v] = b(s,v) <= b(s,u) + w(u,v) – нер-во треугольника

Верно для любых u и vè условие про уменьшение кр. расстояния в алгоритме не сработает на |V|-ой итерации

Б) есть цикл с отриц. Весом

С=<V₀,..,V_k>. V₀=V_k– цикл отриц. Веса

d[V_i] <= d[V_i-1] + w(V_i-1, V_i)_. Просуммируем его от 1 до k.

Т.к. V₀=V_k, то сумма d[V_i-1] = сумме d[V_i] è 0<= сумме w(V_i-1, V_i) < 0 – противоречие è условие в алгоритме – сработает.

Чтд