UnsignedFactorial (unsignedn)

{

unsignedi = 0; //Текущеезначениеi

unsignedF = 1; // Текущее значениеi!

while (i< n)

{

++ i; //i = i + 1

F *= i; // F = F * i- текущеезначениеi!

}

returnF; // Возвращаем значение n!

}

Недостатком этой реализации является то, что с помощью этой функции можно вычислить n!только для nот 0 до 12. Значение 13! уже выходит за верхнюю границу диапазона значений типа unsigned и функция начинает возвращать неверные значения факториала. Для предотвращения получения неверных значений факториалов модифицируем функцию следующим образом:

Unsigned Factorial (unsigned n)

{

unsignedi = 0; //Текущеезначениеi

unsignedF = 1; // Текущее значениеi!

while (i< n)

{

++ i; //i = i + 1

if (0xffffffffu / i< F ) // 0xffffffffu– максимальноезначениетипаunsigned

{

F = 0;

break;

}

F *= i; // F = F * i- текущеезначениеi!

}

returnF; // Возвращаем значение n!

}

Добавленная проверка обнаруживает ситуацию, когда умножение предыдущего значения факториала на следующее значение iприведет к выходу полученного значения произведения за верхнюю границу диапазона значений типа unsigned. В этом случае значению факториала присваивается значение 0(факториал любого числа всегда больше 0), и с помощью инструкции break выполнение цикла прерывается. В этом случае функция вернет значение 0.

При такой реализации функцию Factorialв программе можно использовать, например, так:

unsigned F, n;

…..

if (F = Factorial (n))

….. // Используем вычисленное значение факториала F

Else

cout<< “Ошибка. Факториал числа ” <<n<< “ не может быть вычислен! \n”;

Важно. При рекуррентном накоплении сумм, произведений (степеней, факториалов) целых типов следует очень внимательно контролировать возможность выхода за границы диапазона значений используемого целого типа данных. При возникновении таких ситуаций поведение программы будет непредсказуемым.

Еще один пример. Требуется подсчитать сумму первых nэлементов следующего степенного ряда:

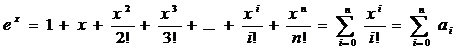
Если подойти к решению этой задачи “в лоб”, то получится следующая весьма неэффективная программа:

intn = 20; //Количество суммируемых элементов ряда

doublex = 2.5; //Значение аргумента x

doubleS = 0; //Начальное значение суммы ряда

inti = 0; // Начальное значение индекса элемента ряда

while (i< n)

{

S = S + pow(x, i) / Factorial (i);

++ i;

}

cout<< “Сумма первых ” <<i<< “ элементов ряда равна ” <<S<<endl;

Неэффективность этого варианта реализации объясняется двумя причинами. Во-первых, поскольку функция вычисления факториала представляет собой цикл, общее количество операций будет быстро расти с увеличением n. Во-вторых, нам вообще не удастся подсчитать сумму более чем 13 элементов этого ряда, так как при i = 13, функция вычисления факториала возвратит значение 0, и наша программа аварийно завершится с ошибкой “Деление на 0”. Избежать аварийного завершения программы можно, как это было описано выше – путем проверки значения факториала на 0 и прерывания цикла, однако более 13 элементов ряда все равно просуммировать не удастся.

Решить эту проблему поможет еще одно рекуррентное соотношение, связывающее очередное значение элемента ряда с его предыдущим значением.

Несложно заметить, что 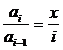откуда следует, что 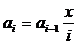при .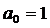

Тогда можно предложить следующий вариант реализации:

intn = 20; //Количество суммируемых элементов ряда

doublex = 2.5; //Значение аргумента x

doublea = 1;// Значение первого элемента ряда

doubleS = 1; //Начальное значение суммы ряда при i = 0

inti = 1; // Начальное значение индекса элемента ряда

while (i< n)

{

a = a * x / i ;

S = S + a;

++ i;

}

cout<< “Суммапервых ” <<i<< “ элементоврядаравна ” << S <<endl;

В этой реализации недостатки предыдущего варианта программы отсутствуют. Удалось избавиться и от вычисления факториала, и от возведения в степень аргумента x. Теперь количество операций на каждой итерации постоянно и равно 4. Программа позволяет находить сумму практически любого количества элементов ряда.

Более сложный вариант рекуррентного соотношения. Требуется написать функцию для получения значения многочлена Чебышева первого рода степени n>= 0, задающегося следующим рекуррентным соотношением:

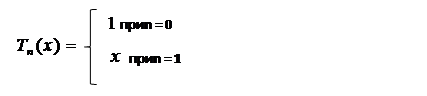
Реализация:

double Cheb_1 (double x, int n)

{

doubleTn, Tn_1 = x, Tn_2 = 1;

Switch (n)

{

case 0: return Tn_2;

case 1: return Tn_1;

default:

inti = 2;

while (i< = n)

{

Tn = 2 * x * Tn_1 - Tn_2;

Tn_2 = Tn_1;

Tn_1 = Tn;

++ i;

}

returnTn;

}

}

При выполнении рекуррентных вычислений с вещественными значениями беспокоиться о переполнении значений вещественного диапазона приходится очень редко (особенно при использовании типа double). Но и здесь встречаются некоторые “подводные камни”.

Предостережение № 1. При определении условия продолжения цикла никогда не используйте проверку на точное равенствовещественных значений с помощью операции ==(впрочем, и в других условиях тоже). Например:

doublea = 1.1, b = 0;

while ( ! (b == a) )

{

b = b + 0.1;

}

Такой цикл никогда не закончится, так как из-за погрешностей вычислений и представления вещественных значений точного равенства aи b при выбранных значениях никогда не будет (так, по крайней мере, происходит для этого примера в MSVisualC++ 2010). Лучшесделатьтак:

double a = 1.11, b = 0;

while ( b <= a )

{

b = b + 0.1;

}

Здесь цикл закончится гарантированно, и последнее значение b будет очень близко к 1.1.

Предостережение № 2.Остерегайтесь складывать (вычитать) очень большие и относительно малыевещественные значения. Например:

double a = 1e20, b = a, d = 1000;

inti = 1;

for ( inti = 1; i<= 1000000; ++ i)

{

b = b + d;

}

cout<< b – a <<endl;

Ожидается, что значение b после окончания цикла будет больше a на 1 000 000 000, однако разность между b иaоказывается равной 0. Это происходит, потому что величина d = 1 000 по отношению к значению a = 1e20 оказывается пренебрежимо малой из-за дискретности представления вещественных значений.

Если увеличить значение d и сделать его равным 10 000, то разность b – aокажется равной приблизительно 1.64e10, а не 1e10как это следует из арифметики – достаточно грубая ошибка.

Для того, чтобы избавиться от этой неприятности, можно поступить так:

double a = 1e20, b = a, d = 1000, s = 0;

inti = 1;

for ( inti = 1; i<= 1000000; ++ i)

{

s = s + d;

}

b = b + s;

cout<< b – a <<endl;

Вот теперь мы увидим то, что ожидалось (или очень близкое к тому) и в первом и во втором случаях. Здесь мы сначала накопили отдельно сумму s относительно малых величин d, а затем уже относительно большое значениеs добавили к b.

48. Понятие инварианта цикла.

Инвариантом называется логическое выражение, истинное перед началом выполнения цикла и после каждого прохода тела цикла, зависящее от переменных, изменяющихся в теле цикла.

Инварианты используются для доказательства правильности выполнения цикла, а также при проектировании и оптимизации циклических алгоритмов.

Порядок доказательства работоспособности цикла с помощью инварианта сводится к следующему:

1. Доказывается, что выражение инварианта истинно перед началом цикла сразу после инициализации параметров цикла.

2. Доказывается, что выражение инварианта сохраняет свою истинность до и после выполнения тела цикла; таким образом, по индукции, доказывается, что по завершении цикла инвариант будет выполняться.

3. Доказывается, что при истинности инварианта после завершения цикла переменные примут именно те значения, которые требуется получить (это элементарно определяется из выражения инварианта и известных конечных значениях переменных, на которых основывается условие завершения цикла).

4. Доказывается, что цикл завершится, то есть условие завершения рано или поздно будет выполнено.

5. Истинность утверждений, доказанных на предыдущих этапах, однозначно свидетельствует о том, что цикл выполнится за конечное время и даст желаемый результат.

Инварианты используют не только для доказательства корректности циклов, но и при проектировании и оптимизации циклических алгоритмов.

Рассмотрим использование инварианта на примере реализации алгоритма Евклида для нахождения наибольшего общего делителя двух чисел.

Постановка задачи. Требуется найти наибольший общий делитель dдвух целых чисел n и m: d =НОД(n, m).

Сформулируем инвариант цикла для нахождения НОД(n, m)следующим образом: пусть имеется пара чисел aи b таких, что НОД(a, b) = НОД(n, m). На каждом шаге цикла будем переходить к другой паре чисел aи b таких, что НОД(a, b) = НОД(n, m). И так будем продолжать до тех пор, пока значение НОД не станет очевидным. Таким образом, инвариант цикла сформулируем так:НОД(a, b) = НОД(n, m). Теперь стоит задача: как найти очередную пару чисел aи b, при которых значение инварианта не изменится.

Из математики (теория чисел) известно, что если d =НОД(n, m), то это же значениеd является и НОД(m, r), где r– остаток от деления nна m, то есть НОД(n, m) = НОД(m, r).

Например:НОД(126, 12) = НОД(12, 6) = НОД(6, 0) = 6

Алгоритм решения задачи можно представить так:

1. Начальная инициализация: пусть a = n, b = m. Очевидно, что НОД(a, b) = НОД(n, m).

2. Находим rи делаем a = bи b = r. При этом выражение НОД(a, b) = НОД(n, m)остается справедливым.

3. Как только bстанет равно 0, тогда НОД(a, 0) = НОД(n, m) = a.

Программа, реализующая этот алгоритм:

int r, a = n, b = m;

// Инвариант: НОД(a, b) = НОД(n, m)

// Цикл заканчивается при b = 0, тогда НОД(a, 0) = a

while (b)

{

// Инвариант: НОД(a, b) = НОД(n, m) выполняется

r = a % b;

a = b;

b = r;

// Инвариант: НОД(a, b) = НОД(n, m) выполняется

}

// Инвариант: НОД(a, b) = НОД(n, m) выполняется

cout<< “НОД (“ << n << “, ” << m << “) = ” << a <<endl;

Можно предложить еще один алгоритм решения этой задачи, основанный на том же инварианте, но использующий другой способ нахождения следующей пары aи b: известно, что НОД(n, m) = НОД(n - m, m)приn>mи НОД(n, m) = НОД(n, m - n)приm>n. Например: НОД(126, 12) = НОД(114, 12) = НОД(102, 12)= …= НОД(18, 12) = НОД(6, 12) =НОД(6, 6) = 6. Но этот алгоритм является более затратным по сравнению с предыдущим.

49. Понятие и определение массива.

Массив представляет собой индексированную последовательность однотипных элементов с заранее определенным количеством элементов. Все массивы можно разделить на две группы: одномерные и многомерные.

Аналогом одномерного массива из математики может служить последовательность некоторых элементов с одним индексом: 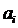при i = 0, 1, 2, … n–одномерный вектор. Каждый элемент такой последовательности представляет собой некоторое значение определенного типа данных. Наглядно одномерный массив можно представить как набор пронумерованных ячеек, в каждой из которых содержится определенное значение:

3.02	1.5	7.0	-2.3	12.0

Это пример одномерного массива из 6 элементов, каждый из которых представляет собой некоторое вещественное значение и каждое из этих значений имеет индекс от 0 до 5.

А вот пример одномерного массива из десяти элементов, представляющих собой одиночные символы:

‘a’	‘b’	‘c’	‘+’	‘1’	‘2’	‘!’	‘#’	‘@’	‘&’

Каждый элемент в этих массивах определяется значением индекса элемента. Например, в последнем массиве элемент с индексом 5 равен символу ‘2’.

Двумерный массив – это последовательность некоторых элементов с двумя индексами: 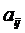при i = 0, 1, 2, … nи j = 0, 1, 2, … m–двумерная матрица. Например, при n = 3 и m = 4:

		j
i

Эта матрица из 3-х строк и 4-х столбцов содержит 3 * 4 = 12 целых значений. Здесь уже каждый элемент определяется значениями двух индексов. Например, элемент с индексом i= 2 и индексом j = 1 равен целому значению 15.

Количество мерностей массивов может быть и больше двух, но при мерности большей 3 наглядно представить такой массив достаточно сложно.

50. Одномерные и многомерные массивы.