Зависимость координаты тела от времени при равномерном прямолинейном движении – x(t)
Способы описания движения
Координатный(график)
Системы отсчета
Уравнение движения тела
Таблица значений
Системы отсчета –совокупность тела отсчета, системы координат и часов
Примеры сами придумайте это легко
Относительность движения - скорость тела зависит от системы отсчета.
Тело может находиться в состоянии покоя относительно одного тела и одновременно - в состоянии движения относительно другого тела. Например, человек, сидящий в кресле летящего самолета, находится в состоянии покоя относительно самолета, но одновременно - в состоянии движения относительно земли. И "виноваты" в этом разные системы отсчета! В этом и состоит относительность движения.
Средняя скорость – это отношение длины пути, пройденного телом, ко времени, за которое этот путь был пройден
Мгновенная скорость –скорость тела в данный момент времени в данной точке
Билет 2
Равномерное прямолинейное движение– движение, при котором материальная точка за любые равные промежутки времени совершает равные перемещения.
 Скорость РПД
Скорость РПД
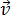 =
= 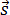 / t
/ t
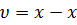 0 / t
0 / t
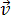 ↑↑
↑↑ 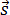
- векторная физическая величина, равная отношению перемещения к промежутку времени, за которое это перемещение совершено.
 Перемещение
Перемещение
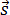 =
= 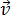 • t
• t
Проекция перемещения на ось ОХ равна:
s = 𝛖t = x – x0
где x0 – начальная координата тела, х – конечная координата тела (или координата тела в любой момент времени)
Уравнение движения, то есть зависимость координаты тела от времени х = х(t), принимает вид:
х = x0 + 𝛖t
Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v < 0), и тогда уравнение движения принимает вид:
х = x0 – 𝛖t
Зависимость проекции скорости тела от времени при равномерном прямолинейном движении - 𝛖x(t); так как скорость постоянна (𝛖= const), то графиком скорости является прямая линия, параллельная оси времени Ot.
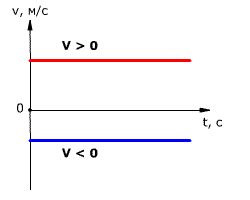
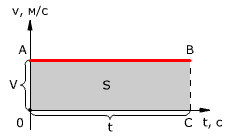
Зависимость проекции перемещения тела от времени при равномерном прямолинейном движении – Sx(t); проекция перемещения на координатную ось численно равна площади прямоугольника ОАВС, так как величина вектора перемещения равна произведению вектора скорости на время, за которое было совершено перемещение.
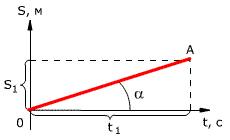
Из графика видно, что проекция скорости равна
𝛖 = s1 / t1 = tg α
где α – угол наклона графика к оси времени.
Чем больше угол α, тем быстрее движется тело, то есть тем больше его скорость (больший путь тело проходит за меньшее время). Тангенс угла наклона касательной к графику зависимости координаты от времени равен скорости:
tg α = 𝛖
Криволинейное движение.Движение по окружности с постоянной по модулю скоростью.Период.Частота.Угловая и линейная скорость.Центростремительное ускорение и тангенциальное ускорение.
Криволинейное движение- движение точки по траектории, не представляющей собою прямую, с произвольным ускорением и произвольной скоростью в любой момент времени.
Угловая и линейная скорость
Линейная скорость-это скорость, с которой тело движется по окружности. Вектор линейной скорости направлен по касательной к окружности вращения. Он перпендикулярен радиусу окружности вращения.
V= 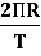 [
[  ](из формулы периода)
](из формулы периода)
Угловой скоростьюдвижения точки по окружности радиусом R называется: отношение угла ϕ поворота радиуса, соединяющего материальную точку с центром окружности, к малому интервалу времени t, за который произошел этот поворот. Угловая скорость обозначается греческой буквой ω
ω = 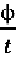 [
[ 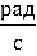 ]
]
Выразив длину дуги окружности через радиус R окружности и центральный угол ϕ, можно ус-тановитьсвязь между угловой и линейной скоростямидвижения материальной точки по окружности:
V= 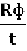 =R ω
=R ω
Вес тела с ускорением
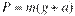 | 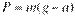 | |
| Когда тело движется с ускорением, направленным вверх, его вес больше силы тяжести | Когда тело движется с ускорением, направленным вниз, его вес меньше силы тяжести |
Невесо́мость — состояние, при котором сила взаимодействия тела с опорой (вес тела), возникающая в связи с гравитационным притяжением, действием других массовых сил, в частности силы инерции, возникающей при ускоренном движении тела, отсутствует.
Перегрузка — отношение абсолютной величины линейного ускорения к ускорению свободного падения на поверхности Земли. Перегрузки возникают в частности при изменении скорости движения транспортного средства (торможении, ускорении или изменении траектории). Общепринятое обозначение — «g». Перегрузка — величина безразмерная. 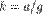
ИСЗ — космический аппарат, вращающийся вокруг Земли по геоцентрической орбите(эллиптической траектории вокруг Земли).
Пе́рвая косми́ческая ско́рость— скорость, которую необходимо придать объекту, который после этого. Иными словами, первая космическая скорость — это минимальная скорость, при которой тело, движущееся горизонтально над поверхностью планеты, не упадёт на неё, а будет двигаться по круговой орбите.
Если мы пренебрегаем высотой, то 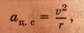
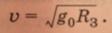 v1= 7,9 км/с
v1= 7,9 км/с
если нет, то 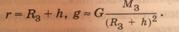

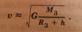
v2=11.2 км/с
Билет 11
Трение - процесс взаимодействия тел при их относительном движении, либо при движении тела в газообразной или жидкой среде.
Сила трения – сила, возникающая при движении или попытке вызвать движение одного тела по поверхности другого и направленная вдоль соприкасающихся поверхностей. Fтр измеряется в ньютонах; Fтр=k*N, где k - коэффициент трения.
Причиной возникновения силы трения являются неровности соприкосающихся поверхностей и взаимное притяжение молекул соприкосающихся тел.
Коэффициент трения - количественная характеристика силы, необходимой для скольжения или движения одного материала по поверхности другого.
Различают силы трения покоя, скольжения и качения.
Трение скольжения - сила, возникающая при поступательном перемещении одного из контактирующих/взаимодействующих тел относительно другого и действующая на это тело в направлении, противоположном направлению скольжения.
Трение покоя – сила, возникающая между двумя контактирующими телами и препятствующая возникновению относительного движения. Эту силу необходимо преодолеть для того, чтобы привести два контактирующих тела в движение друг относительно друга. Возникает при микроперемещениях (например, при деформации) контактирующих тел. Она действует в направлении, противоположном направлению возможного относительного движения.
Трение качения – момент сил, возникающий при качении одного из двух контактирующих/взаимодействующих тел относительно другого.
Примеры полезного трения: торможение автомобиля за счет колес и поверхности земли; трение подошвы обуви о землю при ходьбе.
Примеры вредного трения: изнашивание деталей в механизмах; волочение тяжелой сумки по земле.
Билет 12
Импульс— векторная физическая величина, равная произведению массы тела на его скорость. Измеряется импульс в кг*м/с
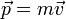 ; P=const, если V=const
; P=const, если V=const
импульс системы тел могут изменить только внешние силы, причем изменение импульса системы пропорционально сумме внешних сил и совпадает с ней по направлению. Внутренние силы, изменяя импульсы отдельных тел системы, не изменяют суммарный импульс системы.
Импульс си́лы— это векторная физическая величина, равная произведению силы на время её действия, мера воздействия силы на тело за данный промежуток времени (в поступательном движении).
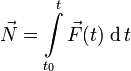
Закон сохранения импульса для замкнутой системы тел:
m1v1 + m2v2 + m3v3=const

Реактивное движение – это движение, возникающее при отделении от тела какой либо части с некоторой скоростью.
Билет 13

Билет 14
1.Работа силы тяжести:
1)Тело движется по горизонтальной поверхности
А=Fтяж*s*cos90®=0
Т.к угол между векторами силы тяжести и перемещения равен 90®, а cos90®=0
2)В начальный момент времени тело находилось на высотеh1 над поверхностью Земли, а в конечный момент времени - на высотеh2 (рис.6.5). Модуль перемещения тела 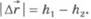 .
.

Направления векторов силы тяжести 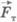 и перемещения
и перемещения 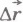 совпадают. Согласно определению работы имеем
совпадают. Согласно определению работы имеем
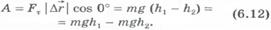
3)тело бросили вертикально вверх из точки, расположенной на высоте h1, над поверхностью Земли, и оно достигло высоты h2 (рис.6.6).
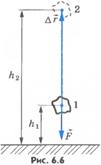
Векторы  и
и  направлены в противоположные стороны, а модуль перемещения
направлены в противоположные стороны, а модуль перемещения 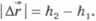 . Работу силы тяжести запишем так:
. Работу силы тяжести запишем так:
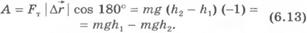
4)Если тело перемещается по прямой так, что направление перемещения составляет угол 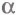 с направлением силы тяжести (рис.6.7), то работа силы тяжести равна:
с направлением силы тяжести (рис.6.7), то работа силы тяжести равна:
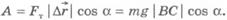
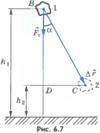
Из прямоугольного треугольника BCD видно, что 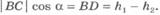 . Следовательно,
. Следовательно,
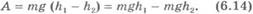
2.Потенциальная энергия в поле тяжести:
Энергия W. тело массой т в поле силы тяжести обладает потенциальной энергией, пропорциональной массе тела. Работа сил электростатического поля А равна изменению потенциальной энергии заряда в электрическом поле, взятому с противоположным знаком:

3.Работа силы упругости:
1)Если пружина растянута, то она действует на шар с силой 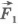 (рис.6.10,б), направленной к положению равновесия шара, в котором пружина не деформирована. Начальное удлинение пружины равно
(рис.6.10,б), направленной к положению равновесия шара, в котором пружина не деформирована. Начальное удлинение пружины равно 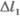 . Модуль перемещения равен:
. Модуль перемещения равен:
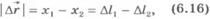
где  - конечное удлинение пружины.
- конечное удлинение пружины.
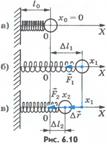
2) Вычислить работу силы упругости по формуле (6.2) нельзя, так как эта формула справедлива лишь для постоянной силы, а сила упругости при изменении деформации пружины не остается постоянной.
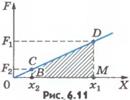
при постоянном значении проекции силы на перемещение точки приложения силы ее работа может быть определена по графику зависимости Fx от x и что эта работа численно равна площади прямоугольника.
В нашем примере работа силы упругости на перемещении точки ее приложения 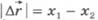 численно равна площади трапеции ВCDM. Следовательно,
численно равна площади трапеции ВCDM. Следовательно,
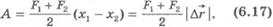
Согласно закону Гука 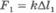 и
и 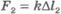 . Подставляя эти выражения для сил в уравнение (6.17) и учитывая, что
. Подставляя эти выражения для сил в уравнение (6.17) и учитывая, что 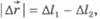 , получим
, получим
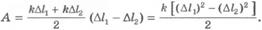
Или окончательно
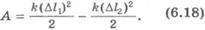
4.Потенциальная энергия упруго деформированного тела:
Потенциальная энергия упруго деформированного тела. Физическая величина, равная половине произведения жесткости тела на квадрат его деформации, называется потенциальной энергией упруго деформированного тела:
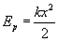 . (20.11)
. (20.11)
Из формул (20.10) и (20.11) следует, что работа силы упругости равна изменению потенциальной энергии упруго деформированного тела, взятому с противоположным знаком:
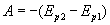 . (20.12)
. (20.12)
Если 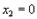 и
и 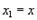 , то, как видно из формул (20.10) и (20.11),
, то, как видно из формул (20.10) и (20.11),
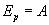 .
.
потенциальная энергия упруго деформированного тела равна работе, которую совершает сила упругости при переходе тела в состояние, в котором деформация равна нулю.
Билет 15
Работа трения покоя. При отсутствии перемещения работа равна нулю, поэтому трение покоя работы не совершает.
Работа трения скольжения.Величина силы трения постоянна и направлена в сторону, противоположную скорости движения. Следовательно, в любой момент времени, в любой точке траектории векторы скорости и силы трения направлены в противоположные стороны, угол между ними равен 180° (cos180° = −1). Таким образом, работа силы трения равна произведению силы трения на длину траектории S:
Amp = −FmpS
Аmp = −μmgS
S = vo2/(2μg)
Кинетическая энергия системы убывает (переходит в тепло)
Мощность
Быстроту выполнения работы в технике характеризуют особой величиной, называемой мощностью.
КПД
Способы описания движения
Координатный(график)
Системы отсчета
Уравнение движения тела
Таблица значений
Системы отсчета –совокупность тела отсчета, системы координат и часов
Примеры сами придумайте это легко
Относительность движения - скорость тела зависит от системы отсчета.
Тело может находиться в состоянии покоя относительно одного тела и одновременно - в состоянии движения относительно другого тела. Например, человек, сидящий в кресле летящего самолета, находится в состоянии покоя относительно самолета, но одновременно - в состоянии движения относительно земли. И "виноваты" в этом разные системы отсчета! В этом и состоит относительность движения.
Средняя скорость – это отношение длины пути, пройденного телом, ко времени, за которое этот путь был пройден
Мгновенная скорость –скорость тела в данный момент времени в данной точке
Билет 2
Равномерное прямолинейное движение– движение, при котором материальная точка за любые равные промежутки времени совершает равные перемещения.
 Скорость РПД
Скорость РПД
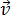 =
= 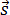 / t
/ t
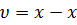 0 / t
0 / t
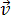 ↑↑
↑↑ 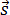
- векторная физическая величина, равная отношению перемещения к промежутку времени, за которое это перемещение совершено.
 Перемещение
Перемещение
 =
=  • t
• t
Проекция перемещения на ось ОХ равна:
s = 𝛖t = x – x0
где x0 – начальная координата тела, х – конечная координата тела (или координата тела в любой момент времени)
Уравнение движения, то есть зависимость координаты тела от времени х = х(t), принимает вид:
х = x0 + 𝛖t
Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v < 0), и тогда уравнение движения принимает вид:
х = x0 – 𝛖t
Зависимость проекции скорости тела от времени при равномерном прямолинейном движении - 𝛖x(t); так как скорость постоянна (𝛖= const), то графиком скорости является прямая линия, параллельная оси времени Ot.

Зависимость проекции перемещения тела от времени при равномерном прямолинейном движении – Sx(t); проекция перемещения на координатную ось численно равна площади прямоугольника ОАВС, так как величина вектора перемещения равна произведению вектора скорости на время, за которое было совершено перемещение.


Из графика видно, что проекция скорости равна
𝛖 = s1 / t1 = tg α
где α – угол наклона графика к оси времени.
Чем больше угол α, тем быстрее движется тело, то есть тем больше его скорость (больший путь тело проходит за меньшее время). Тангенс угла наклона касательной к графику зависимости координаты от времени равен скорости:
tg α = 𝛖
Зависимость координаты тела от времени при равномерном прямолинейном движении – x(t)
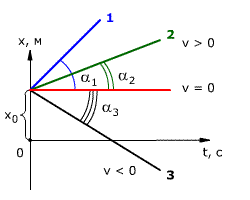
Из рисунка видно, что
tg α1 > tg α2
следовательно, скорость тела 1 выше скорости тела 2 (𝛖1 > 𝛖2).
tg α3 = 𝛖3 < 0
Если тело покоится, то графиком координаты является прямая, параллельная оси времени, то есть
х = х0
Билет 3
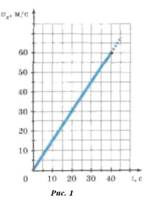
- Равноускоренное прямолинейное движение.
- Равноускоренным называется такое движение, при котором за любые промежутки времени скорость тела изменяется одинаково.
-
 Изменение скорости: V=V-V0 (векторы)
Изменение скорости: V=V-V0 (векторы) - Ускорение - физическая величина, равная отношению изменения мгновенной скорости тела при равноускоренном движении к промежутку времени, за которое это изменение произошло.
- a=дельта V/t или a= V-V0/t
- Равноускоренное движение-простейший частный случай неравномерного движения материальной точки.
- Ускорение показывает, чему равно изменение скорости за 1сек. Ускорение - векторная величина.
-
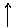
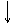 Равнозамедленным можно назвать движение, при котором модуль скорости равномерно уменьшается со временем (если вектора
Равнозамедленным можно назвать движение, при котором модуль скорости равномерно уменьшается со временем (если вектора 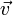 и
и 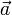 противонаправлены ). Равнозамедленное движение также является равноускоренным.
противонаправлены ). Равнозамедленное движение также является равноускоренным. - Равнопеременное движение. V=V0t+at2/2
-
- Перемещение при РУД.
sx=S1+S2, где S1=V0xt-такое перемещение тело совершило бы, если двигалось равномерно со скоростью V0x.
S2=1/2(axt)*t-приращение перемещения за счет изменения скорости.
Sx=V0xt+1/2(axt)*t
Sx=V0xt+axt2/2
Sx=x-x0, отсюда
X=x0+Voxt+ axt2/2
X(t)~t2, график-парабола
Билет 5
Если тело бросить под углом к горизонту, то в полете на него действуют сила тяжести и сила сопротивления воздуха. Если силой сопротивления пренебречь, то остается единственная сила – сила тяжести. Поэтому вследствие 2-го закона Ньютона тело движется с ускорением, равным ускорению свободного падения 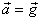 ; проекции ускорения на координатные оси равны ах = 0, ау = -g.
; проекции ускорения на координатные оси равны ах = 0, ау = -g.
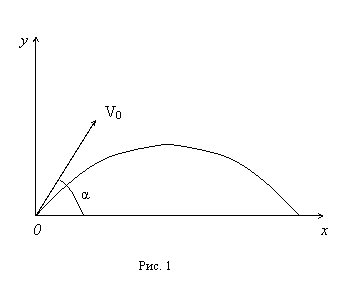
Любое сложное движение материальной точки можно представить как наложение независимых движений вдоль координатных осей, причем в направлении разных осей вид движения может отличаться. В нашем случае движение летящего тела можно представить как наложение двух независимых движений: равномерного движения вдоль горизонтальной оси (оси Х) и равноускоренного движения вдоль вертикальной оси (оси Y) (рис. 1).
Проекции скорости тела, следовательно, изменяются со временем следующим образом:
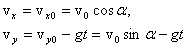 ,
,
где 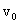 – начальная скорость, α – угол бросания.
– начальная скорость, α – угол бросания.
Координаты тела, следовательно, изменяются так:
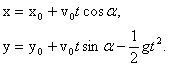
При нашем выборе начала координат начальные координаты 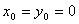 (рис. 1) Тогда
(рис. 1) Тогда
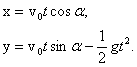 | (1) |
Проанализируем формулы (1). Определим время движения брошенного тела. Для этого положим координату y равной нулю, т.к. в момент приземления высота тела равна нулю. Отсюда получаем для времени полета:
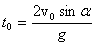 . . | (2) |
Второе значение времени, при котором высота равна нулю, равно нулю, что соответствует моменту бросания, т.е. это значение также имеет физический смысл.
Дальность полета получим из первой формулы (1). Дальность полета – это значение координаты х в конце полета, т.е. в момент времени, равный t0. Подставляя значение (2) в первую формулу (1), получаем:
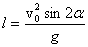 . . | (3) |
Из этой формулы видно, что наибольшая дальность полета достигается при значении угла бросания, равном 45 градусов.
Наибольшую высоту подъема брошенного тела можно получить из второй формулы (1). Для этого нужно подставить в эту формулу значение времени, равное половине времени полета (2), т.к. именно в средней точке траектории высота полета максимальна. Проводя вычисления, получаем
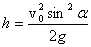 . . | (4) |
Из уравнений (1) можно получить уравнение траектории тела, т.е. уравнение, связывающее координаты х и у тела во время движения. Для этого нужно из первого уравнения (1) выразить время:
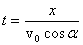
и подставить его во второе уравнение. Тогда получим:
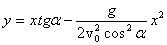 .
.
Это уравнение является уравнением траектории движения. Видно, что это уравнение параболы, расположенной ветвями вниз, о чем говорит знак «-» перед квадратичным слагаемым. Следует иметь в виду, что угол бросания α и его функции – здесь просто константы, т.е. постоянные числа.
Билет 6
