Передача матрицы в качестве параметра функции
Здесь рассматривается этот вопрос без явного использования указателей.
Сначала рассмотрим передачу матрицы в качестве параметра самостоятельной функции без использования класса.
Независимо от того, является ли матрица входной для функции, получается в ней или одновременно входной и выходной, т. е. передаётся в функцию, преобразуется в ней и возвращается в точку вызова, правила передачи двумерного массива в качестве параметра функции одинаковы.
Есть два варианта объявления матрицы в скобках в заголовке функции:
· c помощью явных или предварительно объявленных констант указываем обе размерности: void FunMatr1(…, int M[5][10], int size1,…). В этом варианте обрабатываем либо все (у нас 5) строки, либо меньшее их количество, которое можно, но не обязательно, передать через параметр (size1);
· первую левую размерность можно оставить свободной, т. е. вместо количества строк оставляем пустые скобки. При этом количество столбцов обязательно надо записать: void FunMatr1(…, int M[][10], int size1…). В этом способе, как правило, передаётся в качестве параметра и количество строк (size1), которое используется в соответствующих циклах.
Нельзя оставить свободными обе размерности или одну вторую правую размерность. В таком случае непонятно, где заканчивается предыдущая строка и начинается следующая.
В обоих вариантах в функции необязательно обрабатывать указанное количество столбцов (у нас 10). Его, как и первую размерность, можно также передать в качестве параметра и затем использовать в теле функции:
void FunMatr2(…, int M[][10], int size1, int size2…);
В вызываемой функции (у нас в main) объявляем матрицу int A[5][10], учитывая следующее ограничение: количество столбцов при объявлении должно быть точно таким, как и в заголовке функции. Количество строк может быть меньше, чем в заголовке, например, int A[3][10]. При этом обрабатываться будут три строки (а не пять). При вызове функции в любом случае указываем только имя матрицы без указания размерности и типа её элементов, реальное количество строк и, если надо, столбцов: FunMatr1(…, A, 5, …); или FunMatr2(…, A, 3, 6, …); где 5 и 3 — количество обрабатываемых строк, 6 — количество обрабатываемых столбцов.
Пример. Составим функции для ввода, вывода матрицы и сортировки строк по элементам k –го столбца, где k передаём как параметр функции. При этом содержимое каждой строки не меняется.
const int n2=3;
void INP1(double x[][n2] , int );
void OUT1(double x[][n2], int );
void SORT1(double x[][n2], int , int );
int main()
{ const int size=5; int k;
double a[size][n2]; INP1(a,size);
cout<<"\nOld matrix\n"; OUT1(a,size);
cout <<"\nInput the number of collumn for sorting =>";
while(1) // Ввод номера столбца с проверкой правильности ввода
{ cin>>k;
if (k>=0 && k<n2) break;
cout<<"k>=0 && k<"<<n2<<" Repeat ";
}
SORT1(a,size,k); cout<<"\nMatrix after sorting\n"; OUT1(a,size);
getch(); return 0;
}
void SORT1(double x[][n2], int n, int k)
{ int i,j,m,mn,N;
for (m=0;m<n-1;m++)
{ mn=x[m][k]; N=m;
/*Поиск в k–м столбце минимального элемента, начиная с m–го (mn), и его номера(N).*/
for (i=m+1;i<n;i++)
if (x[i][k]<mn) { mn=x[i][k]; N=i;
}
// Перестановка m–й и N–й строк.
for(j=0;j<n2;j++)
{ double t; t=x[m][j];
x[m][j]=x[N][j]; x[N][j]=t;
}
}
}
void OUT1(double x[][n2], int n)
{ int X,j,Y=wherey();
for (int i=0; i<n; i++, Y++)
for (X=1, j=0; j<n2; j++, X+=7)
{ gotoxy(X,Y); cout<<x[i][j];
}
cout<<endl;
}
void INP1(double x[][n2],int n)
{ for (int i=0; i<n; i++)
for (int j=0; j<n2; j++)
x[i][j]=random(20)-10; }
При работе с матрицей в методах класса необходимо руководствоваться следующими правилами и рекомендациями.
Матрица объявляется в классе в качестве поля с максимальными первой и второй размерностями, в качестве которых можно использовать глобальные константы. Реальное количество строк и столбцов также объявляем, как два поля класса, и определяем их с помощью конструктора. Желательно в нём предусмотреть проверку, не превосходят ли реальные размерности матриц их наибольшие значения.
В методах класса матрица и её размерности в качестве параметров не записываются. Значения элементов матрицы определяются в каком–нибудь из методов класса одним из описанных в § 1 способов.
Для использования методов такого класса создаём объект.
Ту же задачу, что и в предыдущем примере, решим с помощью функций класса:
const unsigned n1max=5, n2max=10;
class MatrClass
{ double x[n1max][n2max]; unsigned size1, size2;
public:
MatrClass (unsigned n1, unsigned n2)
{ if (n1<=0 || n1>n1max) n1=n1max;
if (n2<=0 || n2>n2max) n2=n2max;
size1=n1; size2=n2;
}
void INP1( );
/* Поля класса (матрицу и её две размерности) в качестве параметров методов не записываем! Размерности передаём с помощью конструктора, а матрицу получаем с помощью метода INP1.*/
void OUT1( );
void SORT1( int );
} ;
void MatrClass::INP1()
{ for (int i=0; i<size1; i++)
for (int j=0; j<size2; j++)
x[i][j]=random(20)-10;
}
void MatrClass::SORT1(int k)
{ int i,j,m,mn,N;
for (m=0;m<size1-1;m++)
{ mn=x[m][k]; N=m;
for (i=m+1;i<size1;i++)
if (x[i][k]<mn)
{ mn=x[i][k]; N=i;
}
for(j=0;j<size2;j++)
{ double t; t=x[m][j];
x[m][j]=x[N][j]; x[N][j]=t;
}
}
}
void MatrClass::OUT1()
{ int X,j,Y=wherey();
for (int i=0; i<size1; i++, Y++)
for (X=1, j=0; j<size2; j++, X+=7)
{ gotoxy(X,Y);
cout<<x[i][j];
}
cout<<endl;
}
int main()
{ const int N1=3, N2=6; int k;
MatrClass ObjMatr ( N1, N2);
ObjMatr.INP1(); cout<<"\nOld matrix\n";
ObjMatr.OUT1();
cout <<"\nInput the number of collumn for sorting =>";
//Ввод номера столбца, по которому будем сортировать,
//с контролем ввода
while(1)
{ cin>>k;
if (k>=0 && k<N2) break;
cout<<"k>=0 && k<"<<N2<<" Repeat ";
}
ObjMatr.SORT1(k);
cout<<"\nMatrix after sorting\n";
ObjMatr.OUT1();
getch(); return 0;
}
Задачи и упражнения.
1. Составить следующие функции для работы с матрицей: ввод матрицы; вывод; транспонирование матрицы с сохранением результата на новом месте; умножение исходной матрицы на транспонированную; головную функцию для проверки этих функций:
const int n2=3;
void INP1(double x[][n2] , int );
void OUT1(double x[][n2], int );
void TRANS(double x[][n2], double y[][n2], int );
void MULT(double x[][n2], double y[][n2], double z[][n2], int );
int main()
{ const int size=3; int k;
double a[size][n2],b[size][n2],c[size][n2]; INP1(a,size);
cout<<"\nOld matrix\n"; OUT1(a,size);
TRANS(a,b,size); cout<<"\nTrans matrix \n"; OUT1(b,size);
MULT(a,b,c,size); cout<<"\nMultiplication \n"; OUT1(c,size);
getch(); return 0;
}
void TRANS(double x[][n2], double y[][n2], int n)
{ for(int i=0; i<n; i++)
for(int j=0; j<n2; j++)
y[i][j]=x[j][i];
}
void MULT(double x[][n2], double y[][n2], double z[][n2], int n)
{ int l, i, j, s;
for (i=0; i<n; i++)
for ( j=0; j<n2; j++)
{ s=0;
for (l=0; l<n2; l++)
s+=x[i][l]*y[l][j];
z[i][j]=s;
}
}
void OUT1(double x[][n2], int n)
{ int X,j,Y=wherey();
for (int i=0; i<n; i++, Y++)
for (X=1, j=0; j<n2; j++, X+=7)
{ gotoxy(X,Y);
cout<<x[i][j];
}
cout<<endl;
}
void INP1(double x[][n2],int n)
{ int Y=1,X;
for (int i=0; i<n; i++)
{ Y++; X=-14;
for (int j=0; j<n2; j++)
{ X+=16; gotoxy(X,Y);
cout<<"a["<<i<<","<<j<<"]"<<" ";
cin>>x[i][j];
}
}
}
2. Составить класс для работы с целочисленной матрицей, включив в него матрицу, конкретные текущие размерности и следующие методы: конструктор для ввода и проверки текущих размерностей матрицы; ввод матрицы; вывод матрицы; поиск наибольшего и наименьшего значений матрицы и номеров строк, где они находятся; перестановку двух строк матрицы. В функции main ввести размерности матрицы, создать объект и проверить составленные методы:
const n1max=10, n2max=5;
class ClMatr
{ int a[n1max][n2max], n1, n2;
public:
ClMatr(int size1=5, int size2=3)
{ if (size1>0 && size1<n1max)
n1=size1; else n1=5;
if (size2>0 && size2<n2max)
n2=size2; else n2=3;
}
void MyInp();
void MyOut();
void MaxMin(int &, int &, int &, int &);
void Change(int, int);
};
void ClMatr::MyInp()
{ int x, y=1;
for (int i=0; i<n1; i++)
{ y++; x=-14;
for (int j=0; j<n2; j++)
{ x+=16; gotoxy(x,y);
cout<<"a["<<i<<","<<j<<"]"<<" ";
cin>>a[i][j];
}
}
};
void ClMatr::MyOut()
{ int x, y=wherey()+1, j;
for (int i=0; i<n1; i++, y++)
for (x=1, j=0; j<n2; j++, x+=7)
{ gotoxy(x,y);
cout<<a[i][j];
}
cout<<endl;
}
void ClMatr::MaxMin(int &max, int &Nmax, int &min, int &Nmin)
{ max=min=a[0][0]; Nmax=Nmin=0;
for (int i=0;i<n1;i++)
for (int j=0;j<n2;j++)
if (max<a[i][j])
{ max=a[i][j]; Nmax=i;
}
else if (min>a[i][j])
{ min=a[i][j]; Nmin=i;
}
}
void ClMatr::Change(int k1, int k2)
{ int d;
if (k1!=k2)
for (int j=0; j<n2; j++)
{ d=a[k1][j]; a[k1][j]=a[k2][j];
a[k2][j]=d;
}
}
int main()
{ int n1, n2, Nmax, Nmin, max, min; clrscr();
cout<<"\nn1="; cin>>n1; cout<<" n2="; cin>>n2;
ClMatr ob(n1,n2); clrscr();
ob.MyInp(); cout<<"\nOld matrix\n"; ob.MyOut();
ob.MaxMin(max,Nmax,min,Nmin);
cout<<"Max element= "<<max <<" in "<< Nmax << " row\n";
cout<<"Min element= "<<min <<" in "<< Nmin << " row\n";
if (Nmax!=Nmin)
{ ob.Change(Nmax,Nmin);
cout<<"Matrix after changing "; ob.MyOut();
}
else cout<<"Matrix is not changed \n";
getch(); return 0;
}
Замечания.
1) Во всех задачах предполагается, что матрица имеет фиксированную размерность, при этом количество строк и столбцов — константы.
2) В зависимости от способностей студентов задания выполняются в модульном и (или) объектно–ориентированном стиле, что влияет на оценку. Каждый проект необходимо разделить на несколько функций (методов).
A. Обработка строк матрицы.
1. В каждой строке матрицы найти указанные величины и из них построить один или два одномерных массива, размерности которых соответствуют количеству строк матрицы:
a) среднее значение среди положительных чисел и среднее значение среди отрицательных элементов;
б) второй наибольший элемент и его номер в строке. Если вторых наибольших элементов в строке несколько, найти номер первого из них;
в) сумму чисел до первого положительного числа, включая его;
г) есть ли нуль в строке? Получить 1, если есть, и 0 в противном случае;
д) первый отрицательный элемент и его номер. Если отрицательных чисел в строке нет, получить соответственно 0 и -1.
2. В матрице найти сумму наибольших элементов строк, наибольшую сумму элементов строк и номер такой строки (любой, если несколько строк имеют наибольшую сумму).
3. Найти наибольший среди наименьших элементов строк и наименьший среди наибольших элементов строк.
4. В матрице найти количество строк, у которых:
a) все нули;
б) есть хотя бы один нуль и номер первой такой строки.
5. Дана матрица A, в которой Ai,j — оценка i–го студента на j–м экзамене по 10–балльной системе. Фамилии и названия предметов в памяти не хранятся:
а) найти количество отличников, т. е. количество строк, в которых только 9 и (или) 10. При выводе такие строки выделить другим цветом;
б) найти количество двоечников, т. е. количество строк, в которых есть 1 и (или) 2 и (или) 3.
6. Умножить матрицу на вектор (одномерный массив).
Б. Обработка матрицы по столбцам.
Это же, что и для каждой строки (см. 1), найти для каждого столбца матрицы и построить один или два одномерных массива, размерности которых соответствуют количеству столбцов матрицы.
В. Обработка всей матрицы.
1. Это же, что и для каждой строки (см. 1), т. е. одно или два числа найти для всей матрицы в целом.
2. Даны матрицы A и B одинаковой размерности. Вычислить
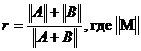¾ наименьшее среди положительных чисел матрицы.
3. Умножить две матрицы, проверив согласованность их размерностей.
Г. Обработка части матрицы (диагонали, треугольника и т. п.).
Дана квадратная целочисленная матрица. Найти количество простых чисел и количество чисел, у которых в двоичной записи нет нулей:
1) на главной диагонали;
2) на побочной диагонали;
3) в левом нижнем треугольнике относительно главной диагонали;
4) в правом нижнем треугольнике относительно побочной диагонали;
5) в верхнем треугольнике относительно главной диагонали;
6) в правом треугольнике относительно побочной диагонали.
Д. Преобразование матрицы, в том числе сортировка.
1. Числа заданной матрицы, принадлежащие отрезку [a, b], увеличить в 100 раз, остальные уменьшить в 2 раза. Измененную матрицу оставить на том же месте.
2. В каждой строке матрицы поменять местами наибольший элемент с наименьшим элементом. Если в строке несколько наибольших элементов и (или) несколько наименьших, то поменять местами первый наибольший с последним наименьшим этой строки.
3. Поменять местами строки матрицы, в которых находятся первое отрицательное число первого столбца и последнее положительное число этого же столбца. Если в первом столбце нет отрицательных чисел, то первую строку матрицы поменять местами с той, в которой находится последнее положительное число первого столбца. Если в первом столбце нет положительных чисел, то последнюю строку матрицы поменять местами с той, в которой находится первое отрицательное число первого столбца.
4. В квадратной матрице поменять местами строку и столбец, на пересечении которых находится наибольший элемент всей матрицы. Если наибольших чисел несколько, то переставить строку с наименьшим индексом со столбцом с наибольшим индексом.
5. Из матрицы “удалить” строку и столбец, на пересечении которых находится наибольший элемент всей матрицы, “подтянув” элементы матрицы к левому верхнему углу. Элементам последней строки и последнего столбца присвоить нулевое значение.
6. Транспонировать квадратную матрицу, оставив новую на том же месте.
7. Каждую строку матрицы рассортировать по возрастанию.
8. Рассортировать строки целочисленной матрицы по следующему параметру строки:
a) количеству четных чисел;
б) количеству чисел, у которых первая слева цифра четная;
в) наибольшей сумме цифр чисел строки;
г) сумме наибольших цифр чисел строки;
д) наибольшему элементу строки.
Замечание. Для решения подобных задач сортировки эффективнее использовать указатели и динамические матрицы, которые рассматриваются во втором семестре.
Е. Построение матриц.
1. Даны два массива A и B одинаковой размерности. Построить квадратную матрицу такой же размерности С, каждый элемент которой определяется по формуле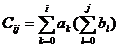 
.
2. Даны две матрицы A и B одинаковой размерности. Построить матрицу С, каждый элемент которой определяетсяпо правилу: 
3. Дан одномерный массив b размерности m. Построить матрицу
.
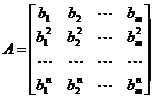