ТЕМА 5. Дифференциальное исчисление функции одной переменной

Лекция № 6.

Тема:Производная функции и дифференциал.

План:

1. Понятие производной функции. Ее физический и геометрический смысл.Понятие дифференциала функции.

2. Основные правила дифференцирования.

3. Таблица производных.

4. Производная сложной функции.

Понятие производной функции. Ее физический и геометрический смысл.

Дифференциал функцииравен произведению производной на дифференциал аргумента независимо от того, является ли этот аргумент независимой переменной или функцией другой независимой переменной.

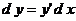
Определение. Производной функции 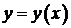в точке 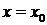называется предел отношения ее приращения в этой точке к вызвавшему его приращению аргумента, когда приращение аргумента стремится к нулю:

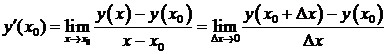или

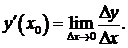
Отсюда 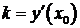– угловой коэффициент касательной к графику функции 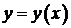в точке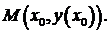

Геометрический смысл производной: производная функции в точке равна угловому коэффициенту касательной к графику функции в этой точке.

Физический смысл производной: производная функции в точке характеризует скорость ее изменения в окрестности этой точки. Отсюда следует, что если 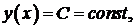то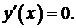

Основные правила дифференцирования.

1. Производная постоянной равна нулю, т. е. c^/=0

2. Производная аргумента равна единицы, т. е. x^/=1

3. Производная алгебраической суммы конечного числа функций равна сумме производных этих функций, (u+v)^/=u^/+v^/

4. Производная от произведения двух дифференцируемых функций равна произведению производно первой функции на вторую плюс произведение первой функции на производную второй функции, т. е. (uv)^/=u^/v+uv^/

5. Производная частного двух дифференцируемых функций вычисляется по формуле: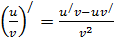

6. Постоянный множитель можно выносить за знак производной, т. е. (cu)^/=cu^/

7. Производная нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные, т.е. (uvw)^/=u^/vw+uv^/w+uvw^/

Таблица производных

	Функция	Производная

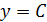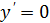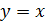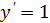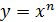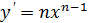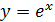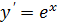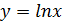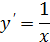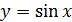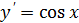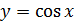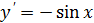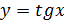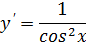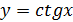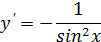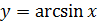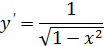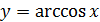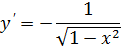Производная сложной функции.

Теорема (о производной сложной функции).

Пусть функция 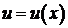дифференцируема в некоторой точке 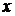, а функция 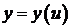дифференцируема в соответствующей точке 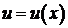, тогда сложная функция 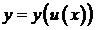дифференцируема в точке 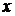и .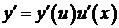

Пример. Найти производную функции .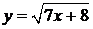

Это сложная функция: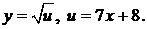

Поэтому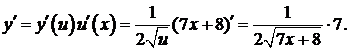

ТЕМА 6. Интегрирование функции одной переменной

Лекция № 7.

Тема:Неопределённое интегрирование.

План:

1. Понятие неопределенного интеграла.

2. Свойства неопределенного интеграла. Таблица интегралов.

3. Замена переменной в неопределенном интеграле

4. Интегрирование по частям в неопределенном интеграле.

5. Интегрирование рациональных дробей.

6. Интегрирование тригонометрических выражений.